春期講習の算数の動画「立体図形」を見ました。
立体図形は6年後半でもしっかりと学びますが、まずは、この単元もしっかりと学習しましょう。想像力を働かせたりする場面も多いですが、たくさん問題を解いて慣れるようにしましょう、頑張りましょう。

子供の時に積み木で遊んでいた子は立体図形の問題が得意になる、って聞きますけど、、、、どうなんでしょうか?
導入と基本①3⃣
おさらいになります。体積は底面積×高さ、です。計算は3.14を最後にまとめて実施します。表面積は、展開図にすると、柱体の側面の体積は長方形になります、長方形の横の長さは10×3.14、となります。これも×3.14はまとめて最後にします。
導入と基本①2⃣
(1)体積は底面積に高さを掛けます。(2)表面積は解き方その1では、3方向から見て考えます、上下と前後と左右でそれぞれを出して、足します。解き方その2では、展開して側面をまとめて考えます、底面2つと、展開した側面の横4×4、縦10、から求めます。
導入と基本③4⃣
回転させます。想像力が大切ですね、分からない人は見取り図を描いてみましょう。円柱から小さい円柱を引いたものになります。(12-1)x3.14,となりますね。
アプローチ①左1⃣
母線と半径の関係がおうぎ形の中心角になります。体積は、底面積×高さ×1/3、となります。表面積は、9x9x3.14+15x15x3.14×9/15、となります。
下記の公式は覚えておきましょう。
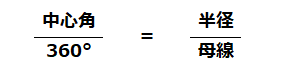
アプローチ①右1⃣
図を想像しましょう、円すいを真っ二つに切ったものになります。体積は6x6x3.14×1/3/x1/2、となります。表面積も同じ様に、全体を求めて半分にしますが、切った断面の面積も忘れないようにしましょう。
アプローチ②左1⃣
上におなじ図形をひっくりかえしてつなげて1つの円柱にして考えます。(1)体積は円柱の半分にして求まります。(2)側面積も同じ様に円柱全体の側面積の半分になります。
アプローチ②左2⃣
先ほどと同じ様に、上におなじ図形をひっくり返してつなげて1つの直方体にします。
アプローチ②右1⃣
展開図を確認しましょう、これは、三角すいを展開したもので、長さによっては、展開すると正方形になる形があります、覚えておきましょう。立体を書いて考えてみましょう。(1)3x3x1/2x6x1/3で求まります。(2)先に底面積を求めます、これは展開図から三角形AMNを求めます。これより、高さが分かります。
アプローチ③左1⃣
回転させた時、半径の比、などを上手く使います。1回転して戻ってくるので、小さい円の円周を1とすると、大きい円は8となります。(1)1:8から、大きい円は半径が80cmとなります。(2)1:5になっているので、計算すると1が16cmとわかります。問題は何cm大きくするか、なので、気をつけましょう。
アプローチ③右1⃣
三角形の相似から、回転数を求めます。円すいの先っぽをつけ足して考えてみます、1:3のピラミッド型の相似の三角形が見えます。これから、大きな円すいは27cmつまり、大きな円の半径が27cmとわかります。転がる小さな円は6なので、6:27から、2:9となり、4.5回転、とわかります。
アプローチ④左1⃣
表面積が分かっています。柱体の側面を1つの長方形としてまとめて求めます。これから底面積が分かり、それから体積も求まります。
アプローチ④右1⃣
長方形から四隅の四角形を除いて、箱を作ります。1つの四角形が25平方数なので、高さは5cmとわかります。底面積を求めるために、側面の長方形4つを考えます、これは5×80=400から分かりますので、底面積は796-400=396とわかり、体積が出せます。
アプローチ⑤左1⃣
内部底辺面を底辺6、高さ8の三角形にして考えます。上と下に三角すいがあります。高さ和が6cmです。
アプローチ⑤左2⃣
正八面体を2つに割って考えます。立体の辺の長さについて、すべての辺の長さは等しいです、面は据えて正三角形です、正三角形8面でできている立体を正八面体、といいます。(1)上ち下に四角すいがあるように内部底面をつくって考えてみます。
アプローチ⑤右1⃣
Lを軸にして回転させます。中心から一番近い点と一番遠い点を回転させます。(1)一番近い点がB、一番通り点がC、と分かります。Bは中心から24cm、Cは25cm離れています。(2)先ほどの面積から高さを掛けた立体を求めます。
アプローチ⑥左1⃣
回転させた後の体積が分かっています。2つの図形が重ならなかった場合は(5×5×10+10×10×5)×3.14=750×3.14、です。2135.2=680×3.14なので、差の70×3.14が重なった部分と分かります。これを5×5×3.14で割ると重なっている高さが求まります。
アプローチ⑥右1⃣
見取り図を描いてみましょう。円すい台2つ分の体積を求めます。三角形の相似使うことで、長さが分かります。(8×8×18×1/3-4×9×9×1/3)×3.14×2、で求めます。補足として、体積の比の利用した解き方の紹介があります。大証の円すい2つを比べると長さの比が1:2なので、体積の比は、たて・横・高さの3方向有るので、長さの比を3回かけます。つまり、(1x1x1):(2x2x2)=1:8です。つまり円すい台は7,になります。この比を使用して求めることができます。
実戦編A1⃣
表面積は3方向(前、左、上)から見て解きます。ただし、隠れて見えていない部分があるので注意が必要です。隠れた要る部分は6㎠が2つあります。
実戦編B1⃣
底面積は小さな半円を移動させて、大きな半円にまとめて計算して体積を求めます。表面積は6x6x1/2×3.14×2+(12×1/2+6)×3.14×8、で求まります。
実戦編B3⃣
半径の長さの比を求めます、これは角度の比と同じになり、6:4:3となります。面積の比は(6×6):(4×4):(3×3)です、これに値を入れて答えを出します。
まとめ
回転させたり、横から見たり上から見たり、と様々な対応が必要となりますが、あわてず、確認しながらがんばりましょう!詳しくは分かりやすいので、動画見ることをお勧めしています。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント