算数の動画「変化のグラフ」を見ました。
グラフからきちんと情報を読み取ることが大切ですね。もちろん比を用いて考えていきます。5年生で習ったことがおおいですが、6年生になって難易度上がってきています!分からない場合は、復習を繰り返しましょう!

グラフの読み取りは、理科にも通じますね
導入と基本①1⃣
底面積の変化の仕方でグラフ変化も変わります。動画では最初に例の説明があります、これを確認したうえで解きましょう。底面積が大きくなるとどうなるかを考えます。円柱は直線になります。底面積が小さいとグラフは急に上がります。だんだんと底面積が大きくなるのは、だんだんと急になるグラフです。
導入と基本①2⃣
グラフの折れ曲がるところが変化するところです。まずは(2)からの解説が分かりやすいです。どの部分も直線なので、円柱、とわかります。底面積はだんだんと細くなることが分かります。(1)aは1分間では0.25cm/分、cは1分間では2cm/分上がります。1分間の水の量は変わらないので、aとcの1分間の高さの比が8:1なら底面積は1:8になります。aはcの何倍ですか、と聞かれていることに注意しましょう。
導入と基本③3⃣
甲のホースだけで水を入れた場合を考えます。(1)段差が緩やかになったところは、グラフが緩やかになるところです。乙ホースを使うとグラフが急になります。(2)10分間では、甲のホースの水の量がわかるので、横の長さが分かります。(3)25分と50分の間のついて考えます。25分で40cm上がるので、1分間で1.6cm上がります。これから水槽がいっぱいになる時間が求まります。体積量で求めていくことも可能ですが、グラフを作成すれば、ピラミッド型の相似の三角形で解くこともできます。
アプローチ①左1⃣
A管,B管の量を求めて解いていきます。(1)A管は1000㎤を5分で入れるので、1000÷5で200㎤ともとまります。(2)A管+B管は、5分から7分で750㎤入った、とわかります。A管の量を引くことを忘れないようにしましょう。(3)A+Bは375㎤、と(2)でだしているので、これを用いて解きます。(4)あと8分で3000㎤はいることから考えます。
アプローチ①右1⃣
Aは水を入れます、Bが水を抜きます、全体として減っていくので、Bの水量の方が多いです。(1)グラフに書きこんで210÷42、で求まります。(2)30分で210ℓ減った、とわかります、これがBとAの差7リットル、とわかります。(3)B管は(2)から求まりますね。
アプローチ②A1⃣
奥行きが同じなので、底面積だけで考えます。水が入る順は、①仕切りの左側→②仕切りの右側→③上側、となります。比を用いると簡単です。(1)分数で計算すると、計算時間を短縮できます。①は12秒かかります。(2)も分数で計算できますが、比を利用すると、横の長さの比3:4なので、時間も正比例するので、②は16秒、と求めることができます。(3)解法その1では容器全体に注目します。全体の容積を9000で割ると求まります。その2では③の部分が14秒かかる、と求めてしまえば、①②③を足すことでもとまります。その3では比の利用をします。③と比べるのに①+②の部分と比べます。高さの比をつかいます。(4)は、グラフを書きますが、中途半端な点も書いておくようにしましょう。②がたまっている時間は水位が変わりません。
アプローチ②B1⃣
①②③④⑤の順で水が溜まります。グラフから、①が10分で入ります。②も10分で入ります。③は①+②が20分なので、高さの比から、③は10分で入るとわかります。④は①+②+③が30分なので、横の比が2:1なので、④は15分で入ります。⑤は①+②+③+④が45分なので、高さの比3:1から⑤は15分かかります。これらをグラフにします。
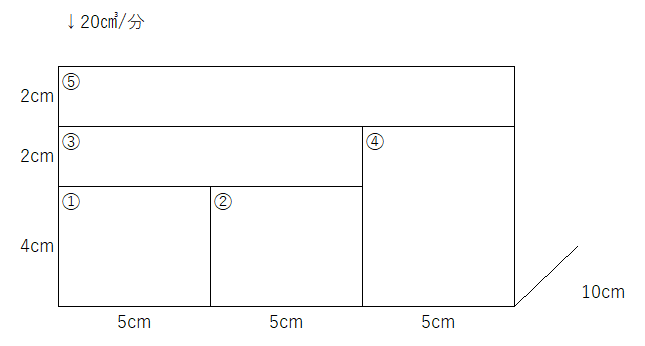
比べる面積の違いとなる比、を確認しながらながら解いていきます。
アプローチ③左1⃣
グラフで分かる部分から解いていきます。60cmの部分が腰掛の高さになります。(1)初めは1分間で5cm水面が上がる。、とわかります。折れ曲がったあとは、2.5cmずつ水面が上がります。16分後なので、折れ曲がった後の計算をします。また、グラフからピラミッド型の相似の三角形を使って解くこともできます。(2)グラフで分かる長さを水槽に書き込みます。右下の部分が12分ではいります、体積もわかるので、水は、12000㎤/分、とわかります。これから上の部分が16分かかるので体積が分かり、高さと縦が分かっているので、横の長さが求まります。補足では、比の利用をします、水面が上がる高さと底面積の逆比で求めることができます。水が1分間で増える量が同じなので、底面積の比が、増える高さの逆比となります。上の部分と下の部分の底面積の比が2:1なので、そのまま横の長さの比も2:1となります。
アプローチ④左1⃣
これも分かる部分から解いていきます。奥行きが分からないので体積を求めることができません、ので、比を使って解きます。補足は全体を見ての考え方です、動画がとても詳しく分かりやすいのでお勧めです。
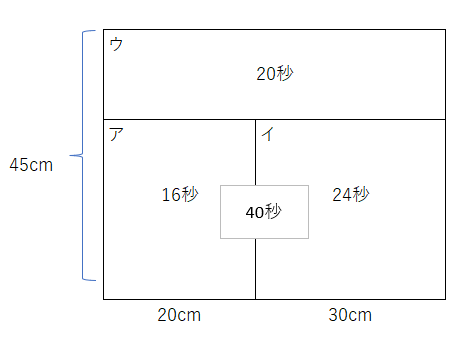
アプローチ④右1⃣
グラフから分かる部分を図に書いていきます。分かりやすいのが上部の15秒なので、そこの比から解きます、高さの1:2から考えます。本当ならア+イが30秒かかるはずですが、25秒です、つまり、この5秒が球の体積とです。
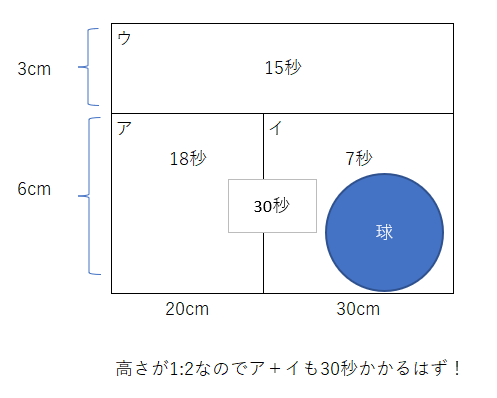
アプローチ⑤A1⃣
グラフの形が違うので、底面積が変わっていることが分かります。水を入れる時は90秒、水を抜くときは120秒かかっているので、時間の比は3:4となります。つまり、同じ容器なので体積は同じです、ので水の入る人出る速さの比は逆比の4:3となります。入るのは1秒間に4、出ていくのは3、とします。仕事算的な考え方で容器全体の大きさを360と置いても構いません。次に横に倒して重ねて見て、各エリアの仕事量を追記すると、それぞれの辺の比が分かりますので、それから求めます。
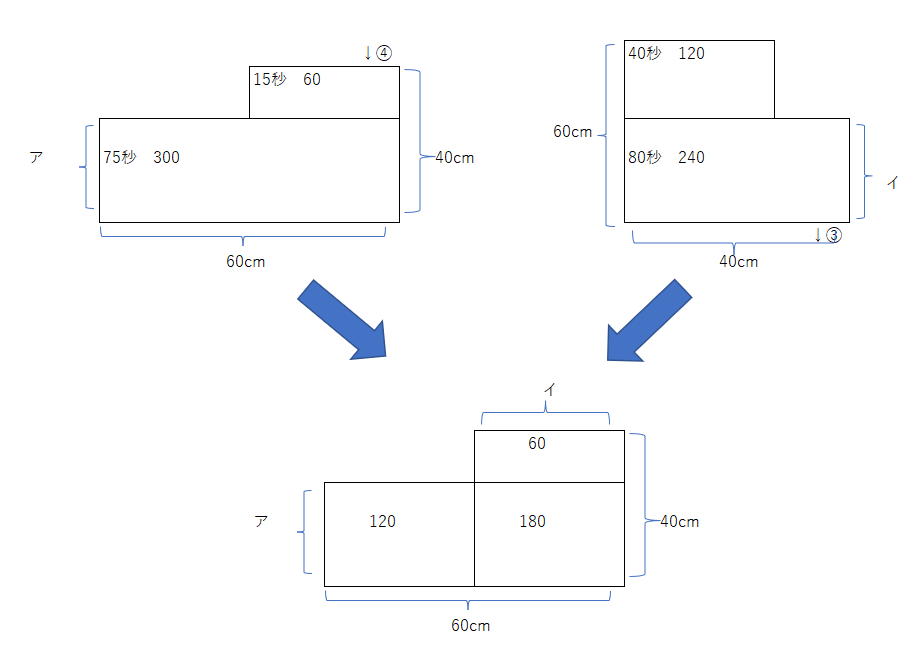
アプローチ⑤B1⃣
グラフから高さの増分を出すことで、底面積の比が逆比なので求まります。(1)1分間に上がる高さは、最初から順に、分数で、1/5cm:1/2cm:1/3cm:1/6cm、なので、底面積の比は逆比になり、下から順に、5:2:3:6となります。そこから下記図のような立体が見えてきますね。形が分かれば、全体をとらえやすくなりますね、先ほどの比を用いて考えます。(3)下から3段目について考えます。単位に気を付けて解きましょう。(4)15cmになるのは下から4段目から上に2cm上がる、と考えます。
アプローチ⑥右1⃣
高さの比は、底面積の逆比、を用います。そしてつるかめ算、で解きます。(1)上の部分は体積を求めることができます、これに10分間かかっているので、水の量を求めることができます。(2)高さの上がる比が、はじめと後で、5:2なので、底面積の比は2:5となります。これから、横の長さの比も5:2となるので、75cmが比5、とわかります。(3)41分間で100cmになれば良いです。はじめは2cmずつ、後は5cmずつ、なので、これは速さのつるかめ算で求まります。
アプローチ⑥左1⃣
円柱が入っています、端に寄せて考えましょう。この問題も水面が上がる速さ、を使って考えます。途中で底面積が変わることを理解して、つるかめ算を用います。(1)はじめは1分間に5cmあがります、円柱をこえた後は1分間に3cmずつ上がります。10分間で39cm上がります。これらから、つるかめ算を用いて解くことができます。(2)前の設問から円柱の高さが22.5cmと出せます。これと、高さの速度が5:3なので、底面積が逆比で3:5となります。
アプローチ⑦1⃣
分けられた箇所が増えますが、考え方は同じです。グラフにある値を図に書き込むと下記になります。
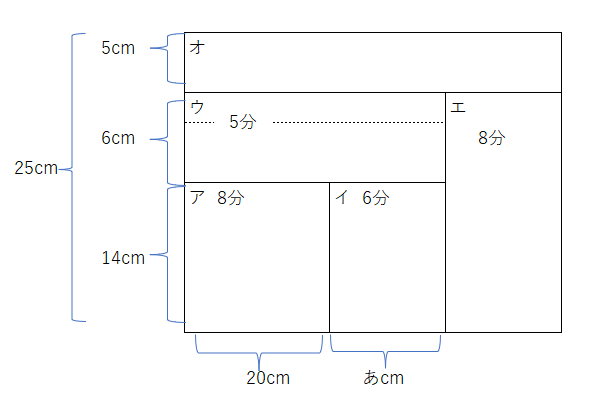
これに最初②、途中で③で水を入れます、仕事を書き込むと下記になりますね。
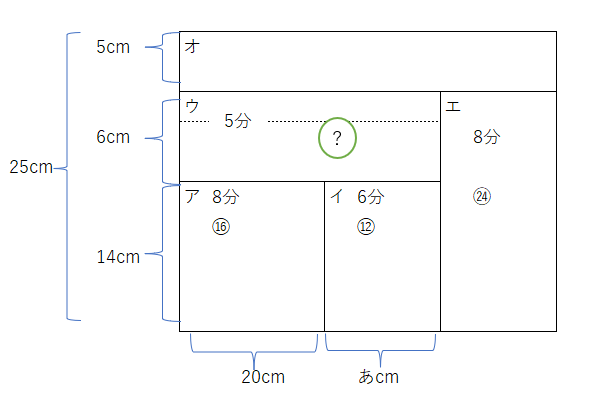
ウの部分は高さの比が3:7なので、ウは⑫とわかるので、つるかめ算から水を②から③に変えたときの時間が分かります。(3)全体で考えます、オと、ア+イ+ウ+エは64、高さの比は1:4から、オが16と分かります。これから何分後か分かります。
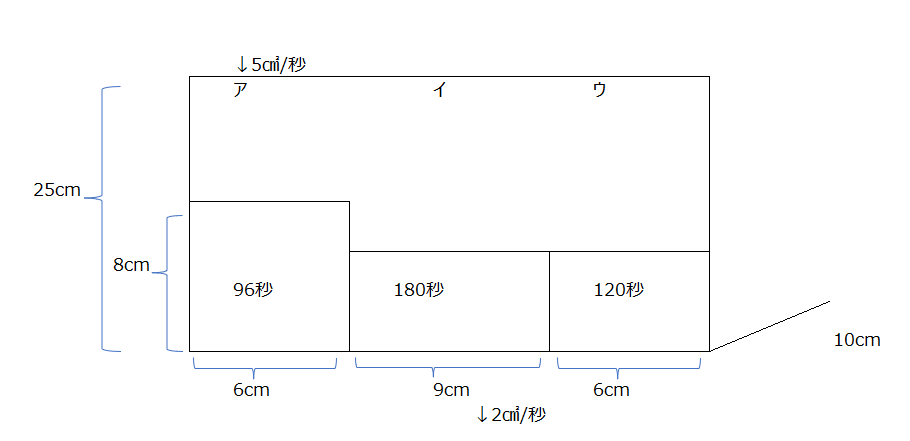
アプローチ⑧1⃣
先程の同じ考え方ですが、水が溜まる順に注意しましょう。アイウに水がたまる時間を最初に求めておきましょう。なかなか複雑で難しいですが、動画では丁寧に分かりやすく説明がありますのでゼhとも参考にしましょう。
今週の立体切断1⃣
あり得ない切断面かどうか、見抜けますか、なかなか難しいですね。図1や図5はありえます。図1は正三角形になります。図5は平行四辺形になります。
図2は立方体の内部を通る切り口になっているのでありえません。図3は同じ面が2つ切り口があるので、ありえません。図4は向かい合う面の切り口が平行になっていません。
苦手な人は動画で確認しておきましょう。
まとめ
途中でつるかめ算を使うことに気づけるひとは算数得意な人です!なかなか難易度は高くなっていますが、変化をグラフで読み取ることは、理科にも出てきますし、この辺りの基本部分は押さえておきたいですね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント