算数の動画「速さ」を見ました。
2時間あります、みっちりと説明して頂いております、つまり、大事な単元なんですよ、きっと!分からないところはしっかり理解するまで動画見てみましょう。比で解くようにしましょう。

解説見ても分からないなら、動画見ましょうね
Simplicity | 内部SEO施策済みのシンプルな無料WordPressテーマ
はじめに
今回は動画での説明の順番が変わっています。導入と基本→実戦編→アプローチ→立体切断、の順番で説明があります。アプローチ編でもたまに順番の変更があります。「学習アドバイス」で確認しながら解き進めましょう。
導入と基本②1⃣
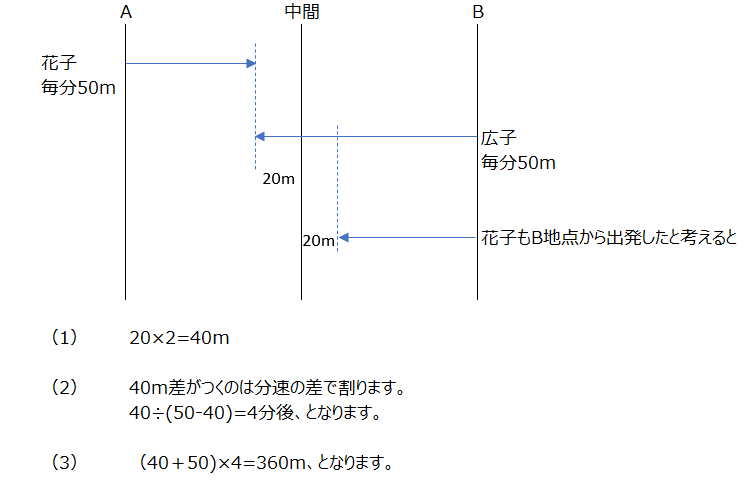
位置関係を図でまとめて考えていきます。まだ、比を使わずに解けますね。
導入と基本②2⃣
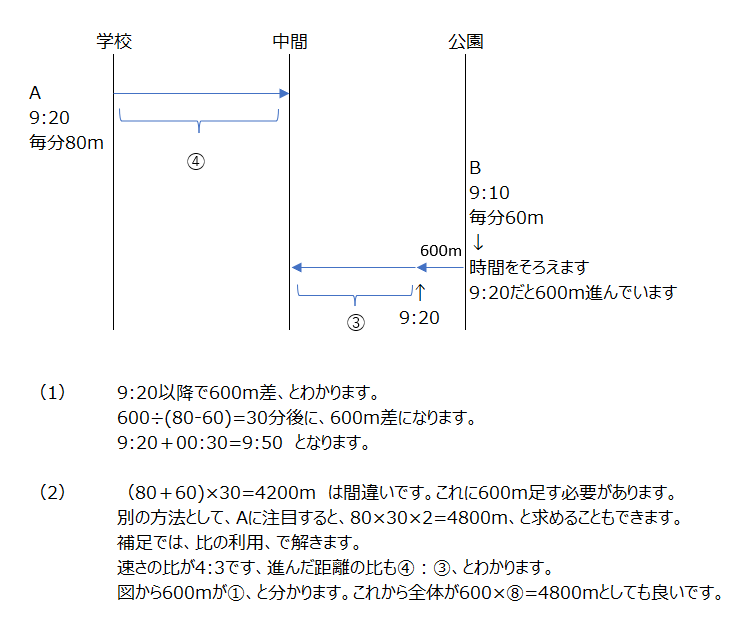
こちらも図に書きます、出発時間を合わせて考えます。ここで比の利用、の別解が補足として教えて頂けます。
導入と基本②3⃣
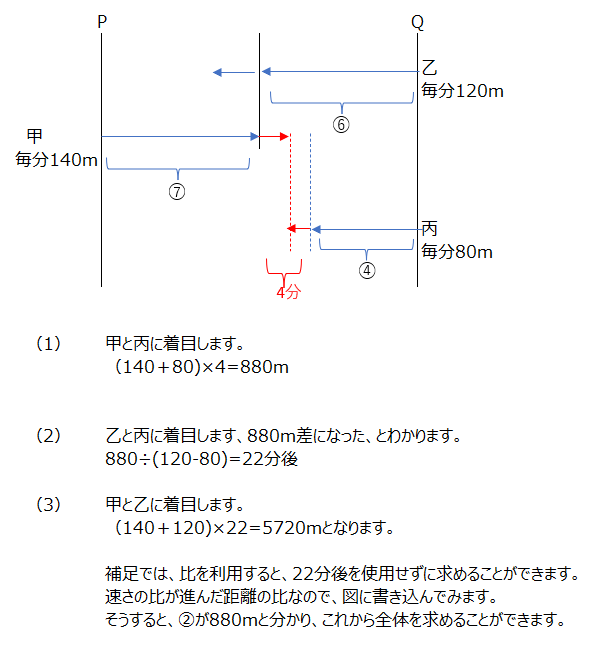
甲乙丙と3人の動きをやっぱり図示化します、(1)は甲乙、(2)は乙丙、(3)は甲丙、に着目して考えていきます。もちろん、比でも解けますよ。補足で説明頂けています。
実戦編B1⃣
2つの時計が1日で何秒差になるか、を考えます。1日で50秒の差がつきます。□日で9分差(540秒差)、と考えると、秒は10.8倍になっているので、□は10.8日経った、と分かります。0.8日は0.8×24=19.2時間、とわかります。0.2時間は、0.2×60=12分です。つまり、10日と19時間12分後、とわかりますので、これを2月1日10時に足すt、2月11日、29時12分、となり、時間を繰り上げると2月12日5時12分、と分かります。答える時は、2月12日午前5時12分、と書きましょう。
実戦編C1⃣
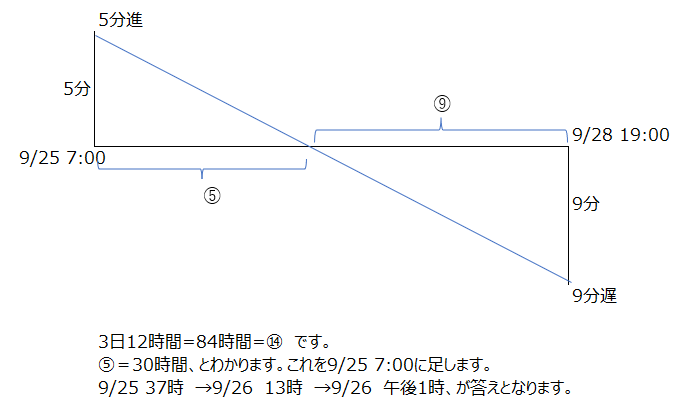
正確な時計と、遅れていく時計の問題です。図で説明しています、砂時計の相似の三角形で解けます、この辺りの複合的な考え方は面白いですね。
アプローチ①右1⃣
比でまとめて解きます。速さと時間の比は逆比ですね、その差が何分か、から求めていきます。

アプローチ①左1⃣
出発時間がずれているので、合わせてから考えます。

アプローチ②左1⃣
速さと時間の逆比の差、から考えます。単位に気を付けて計算します。
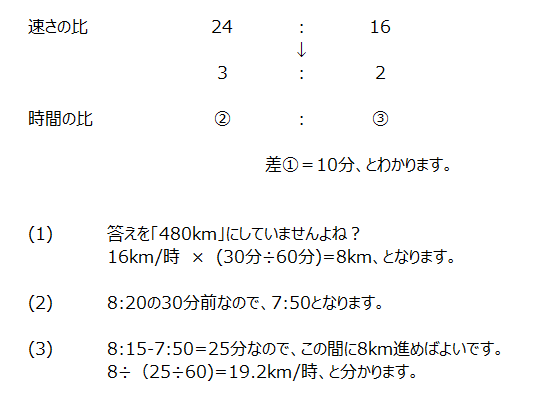
アプローチ②右1⃣
途中で速さが変わります、図に書いた説明が分かりやすいですね、なにが同じか、から一つずつ探して分かる部分を図に書いていきますよ。
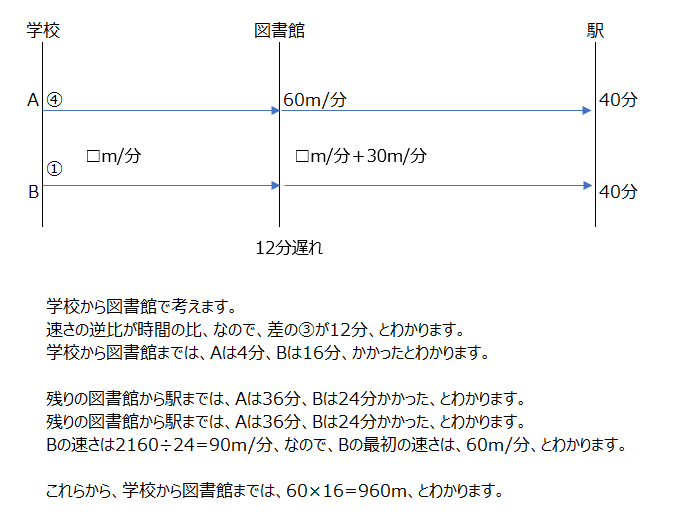
アプローチ④左1⃣
引き返して2回目に会います、つまり、2回目に合う時は、2人が進んだ距離の合計は2倍なのですね、それぞれが進んだ距離も2倍、出会うまでにかかった時間も2倍、です。この辺りはテクニックですね、知ってると解くのが早くなります。
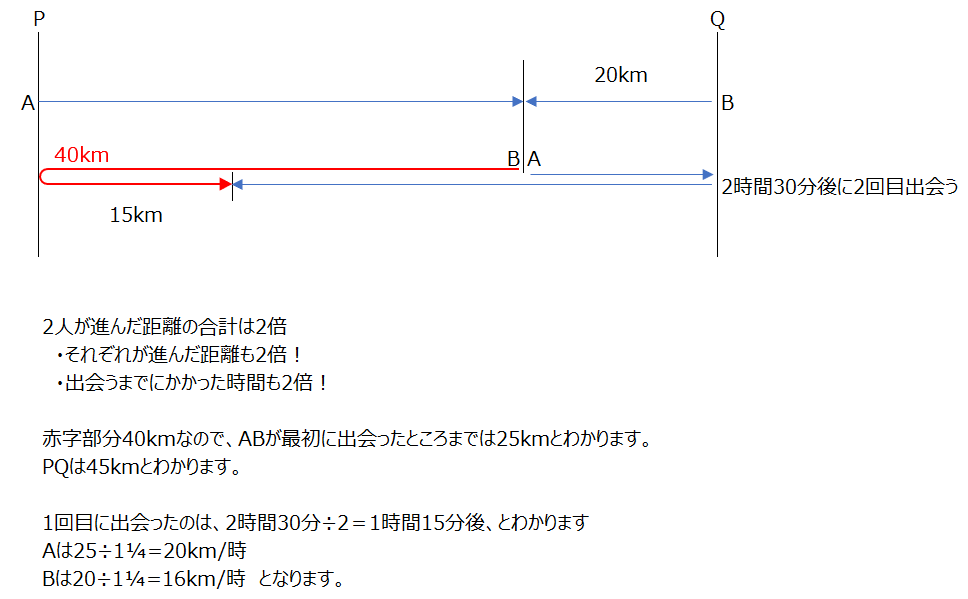
アプローチ④右1⃣
上の問題と同じように、距離が2倍となることをつかって考えます。
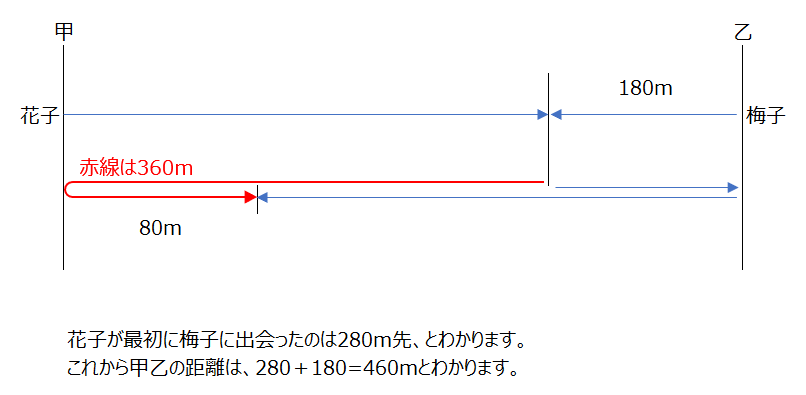
アプローチ⑤左1⃣
同じように解いていきますが、比で解いていきます。
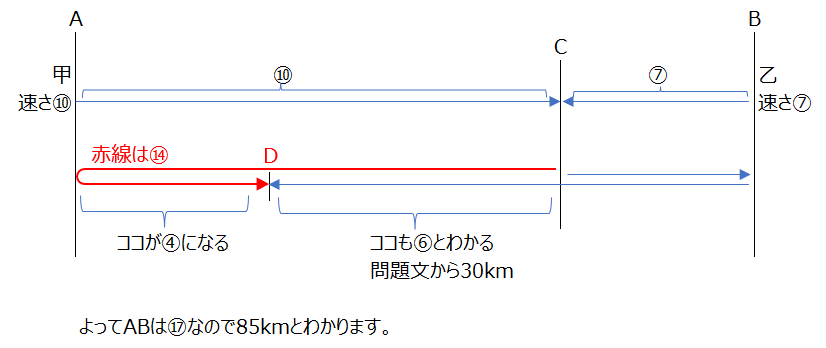
アプローチ⑤右1⃣
目的地から引き返してくる問題です、比を使いますが、どこの距離が何分かかったか、など間違えないように解いていきます、動画、分かりやすいですね。
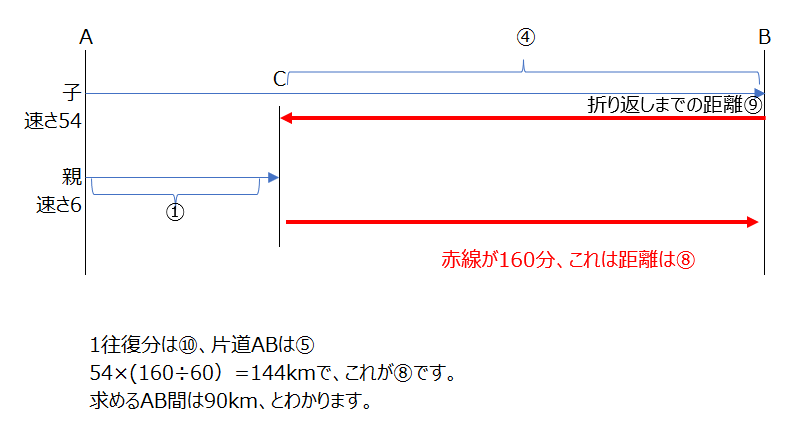
アプローチ③左1⃣
ABCの3人出てきます、まずは、AとCで考えて、次にBとAで考えてみます。そうすると、同じ比が使えることが分かります、これも、動画がとても分かりやすく説明して頂いていますよ。ややこしいですが、ひとつずつ考えるとわかりやすい!
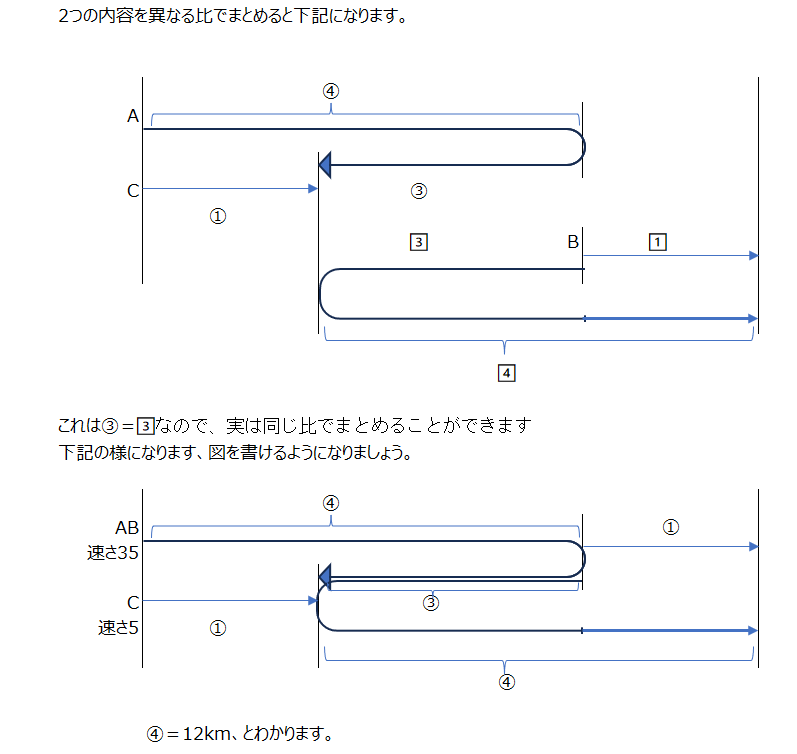
アプローチ③右1⃣
同じ様に、ABCで同じ比が使えます。長さの分かる部分が比ではいくらか、を出すのがポイントです。
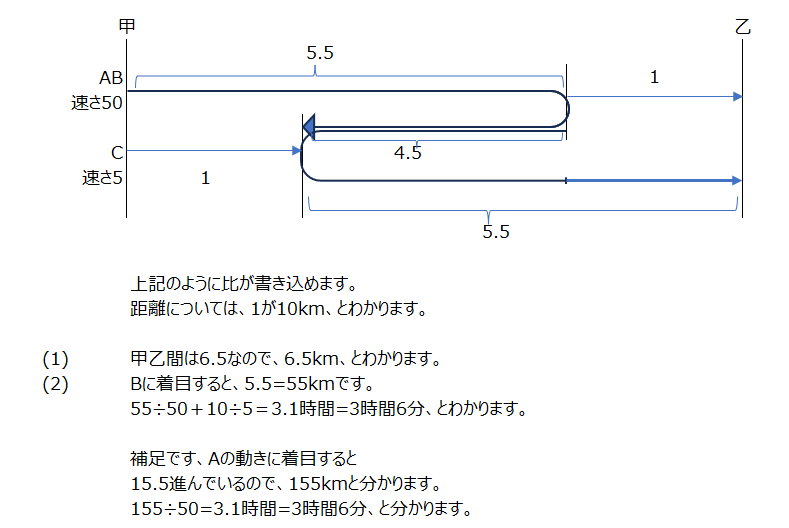
アプローチ⑥左1⃣
行きと帰りの途中で休憩していく問題です。行きと帰りの周期を考えます。この周期の切れ目の部分の考え方を間違えないようにします。

アプローチ⑥右1⃣
最後の休憩をするかしないか、の問題が(1)です、間違えないようにしましょう!次郎が休んでいる時間が12:45~13:00であることを求めて考えていきます。

アプローチ⑦A1⃣
PとQの速さです。(1)はPがBから出発する20秒後の状況を考えます。(2)では35秒後の図で考えます。(3)は40秒後で考えますよ。

グラフを用いて考えていく説明を動画でして頂いています。こちらの方が視覚的には分かりやすいかもしれませんね。動画で説明を確認してみましょう。
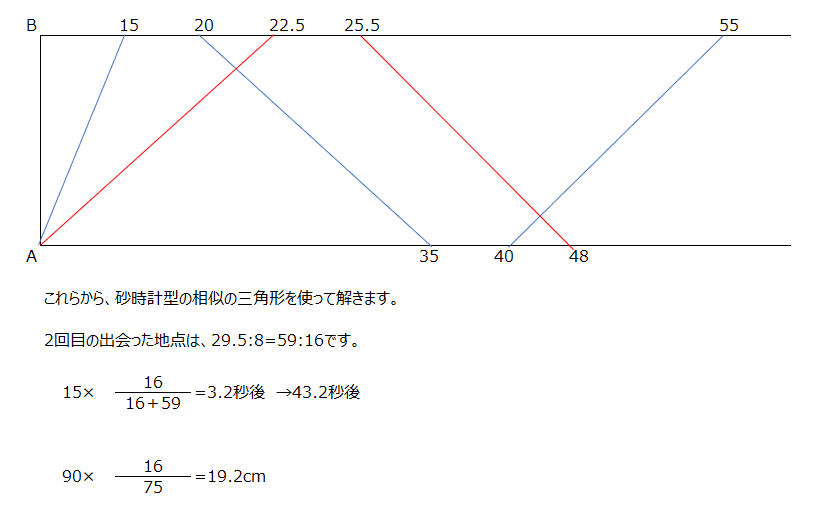
アプローチ⑦B1⃣
Pは4秒周期、Qha8秒周期です。周期で考えると8秒周期で54cm近づく、と分かります。この8秒を何回繰り返すかで考えます。間違った考え方として、1秒で54÷8=6¾cmずつ近づく、としないようにします、1秒後で考えると10cm近づいていますので、間違いに気づけます。(1)120÷54=2回・・・12cmです。この12は、12÷(4+6)=1.2秒、と考えます、余りには気を付けましょう。これらから、8秒×2回+1.2=17.2秒後、とわかります。(2)Pは24×2回+4×1.2=52.8cm、と分かります。
アプローチ⑦B2⃣
途中までは、先程と同じような問題です。余りの時間が、Qしか動いていない、という所が違うため難しくなっています。(1)270÷116=2回・・・38cm、となります。38÷(4+8)=3⅙秒、です。38-(4+8)×3=2cm、はQしか動いていません。ので、2÷8=¼秒、から全部足して、12×2+3+¼=27¼秒となります。(2)Pは36×2回+4×3=84cm、となります。
アプローチ⑧A1⃣
時計の問題です、正しい時間と遅れる時計の時間を比で解いていきます。(1)和子さんの時計は、24時間で30分遅れます。正しい時間7.5時間で、和子さんの時計は□分遅れる、と考えると、9⅜分遅れる、とわかります。ので、これを7:30から引いて求まります。「とけいが何時何分をさしているのか」を答えるので、「午後」は書かなくてもいいです。(2)は花子さんの時計は、正しい時間24時間で40分進みます。花子さんの時計が10時間経ったとき、です、正しい時計が10時間経ったのではないです。花子の時計が何時か、の情報をから比を使って解き進めます。正しい時計:花子の時計=24:24⅔=36:37、となります。比37が10時間ですので、比36を計算すると、9時間43と29/37分後、と分かります。問題文に「その日の午後」と明記されていますが、「時刻」が問われているので、一応「午後」と書いておきます。
動画では計算の工夫の説明がありますね、こちらの方が計算楽ですね。
アプローチ⑧B1⃣
列車の発着時間と、ABのくるった時計、の問題です。解法1では、問題文を動画の様に示すと理解が深まって解きやすくなりますね。何と何の時間を比で求めていくか、です、難易度高いです。
解法2では、算数がものすごく得意な人向けの説明があります。レベル高いです。一度は見ておいても良いかもしれませんね。
今週の立体図形
(1)三角柱の体積を求めます。6×3÷2×6、で求まります。(2)砂時計の相似の三角形を使用します。6×3÷2×⅔、で求まります。(3)三角すいの体積を求めます。(4)(1)で求めた立体から(3)で求めた三角すいを引けば求まります。
まとめ
速さ、の単元ですが、単純な速さの計算だけではなく、時計だったり、比だったり、図形で解いたり、と解き方は多種多様です。どの解法で解くのか、が分かるかどうかがが、算数できるかできないかの違いなのでしょうかね。頑張ってたくさん解いて、慣れるようにしましょう~
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント