算数の動画「速さ(2)」を見ました。
速さの比や距離の比、の逆比が、掛かった時間の比、になります。これらのどれかの比を使って比較して、問題文で与えられている数値(時間や距離)と当てはめて解いていく感じは前からと変わりませんね。流水算などはテクニックを覚えてしまうのもありですね。

具体的な数値が、どの比に当たるか、を調べて解いていきます。
導入と基本①4⃣
昔に学んだ流水算です、ただ、速さの比から、逆比で時間の比を求めて、差の比がxx時間、と分かり解いていきます。つまり比で求めます。川の流れは、上りと下りの速さの差を2で割ります。

導入と基本③3⃣
速さの比から同じ時間で進んだ距離の比が分かります。具体的な数字が時間で出ていますので、これに着目しましょう。
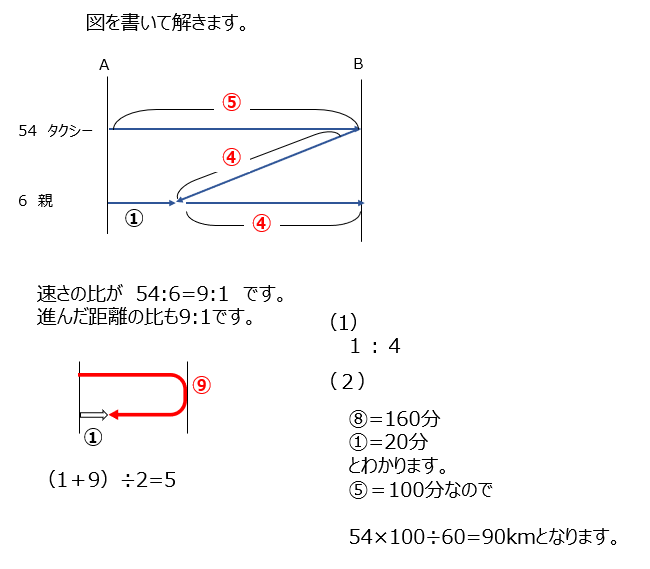
導入と基本③4⃣
途中で引き返す問題です。図に書いてどこが同じかを理解します。速さ変わらずに同じ距離を同時につくので、歩く距離は同じですね、覚えておくと楽ですね。
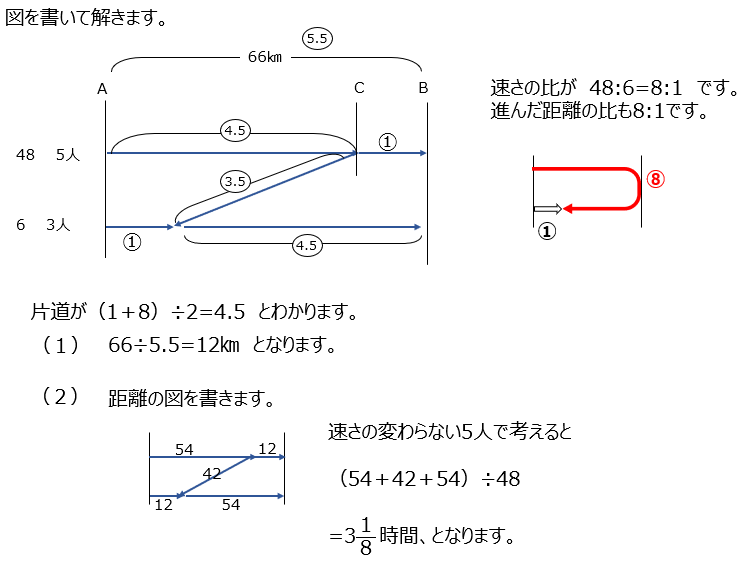
アプローチ①左1⃣
A B間を120とおいて考えますよ、答え方はキチンと問題文を確認しましょうね。

アプローチ①右1⃣
同じ距離を進むのにかかる時間を求めます。時間の比から、速さの比も分かりますね。
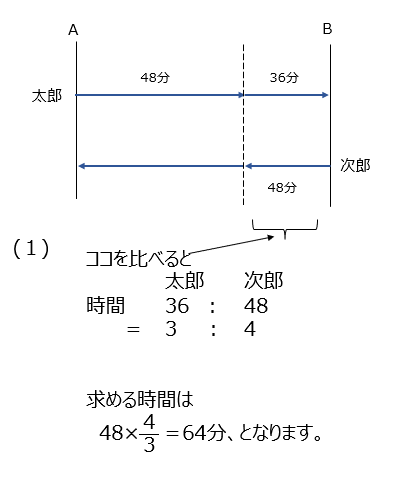
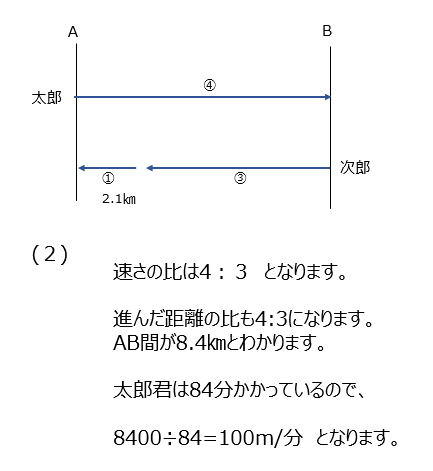
アプローチ②左1⃣
静水時の速さ、流水の速さ、の問題です。静水時の比と流水の速さを足したものがAとBはわかりますので、引き算して流水の速さを消せますね。

アプローチ②右1⃣
流水算です、比を使ってときますよ。上りと下りで二つ式ができますよね。平均の速さ=進んだ距離の合計÷かかった時間の合計 ですよ。


アプローチ③左1⃣
予定と実際で線分図を書きます、渋滞していた時の時間が分かりますね。予定していた時間を1として解いていきます。
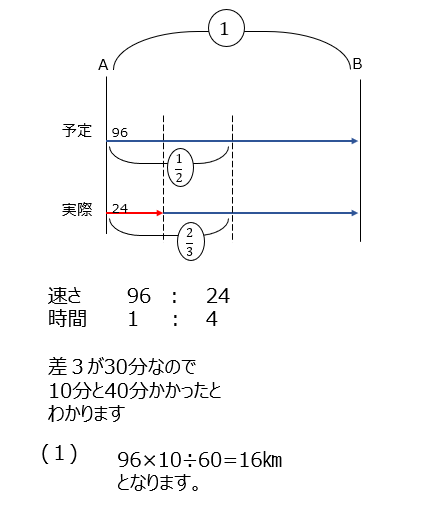

アプローチ③右1⃣
平らな道と上りと下りでの速さを比や時間の比で求めます、動画では図示しながらの説明となっていますので分からないので方は見てみましょう!
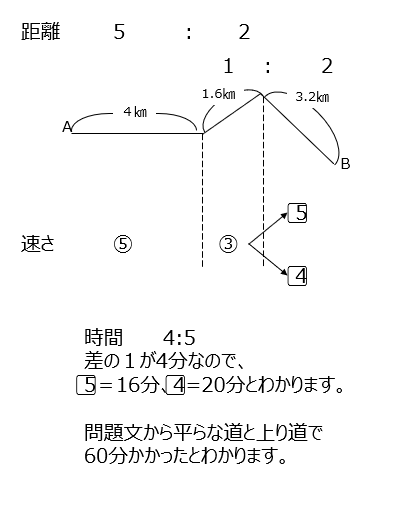

アプローチ④左1⃣
問題文から式を作ります。BとCの比率がわかるのでそこからさかのぼっていくと、Aと Cの比率がわかりますよ。

アプローチ⑤A1⃣
円周を3つの点が動きます。一周の長さを90とおいて考えます。3つ重なるのは、最小公倍数で解きます。


アプローチ④1⃣
3点が動いて、正三角形になります。それぞれが20cm離れている状況を確認します。最小公倍数20秒毎にどの様な位置になってるかを確認します。別解として、1点を止めて、2点の動きを追う方法の紹介があります。補足として、1周を3区画に分けて考えることもできますよ。

おまけの問題では、2度目、3度目に正三角形になるタイミングを聞かれています、単純に40秒後、60秒後はならないですよ、、、

アプローチ⑤B1⃣
AとBとCの動きをまとめます。追い抜いた地点以降は、比では同じなので、後は計算だけですね。導入と基本にも説明あったよくある問題ですね〜
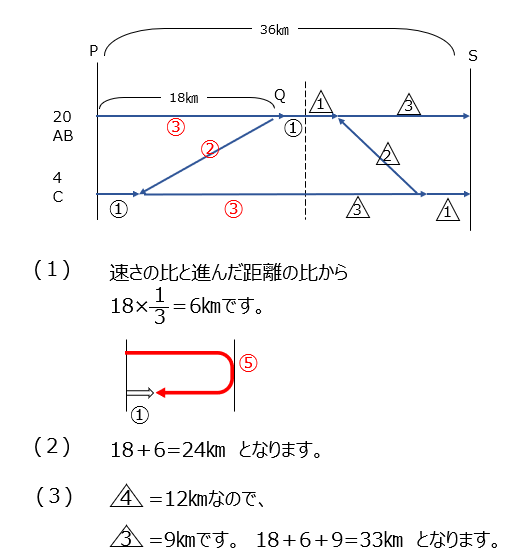
アプローチ⑥左1⃣
先程と同じ様な問題です、同じ時間に進んだ距離から考えますよ。BとCの歩く速さが違うので、図は点対象にならないです。個別に比を出していくと、Aが引き返した距離の比を合わせることができます。そこから全体の比を合わせて解いていきますよ。
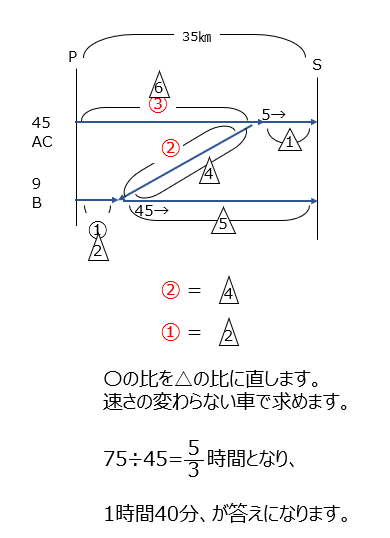
アプローチ⑥右1⃣
問題文を式にしていきます、一周の距離を最小公倍数の630にすると計算が楽になりますね。(3)では、Cを止めて正三角形になる事を考えます。

アプローチ⑦左1⃣
進むオートバイからの音の跳ね返りの問題ですね、図にキチンと書き込めましたか?音の跳ね返りの差の部分が、オートバイのどの部分に当たるかを考えますよ。
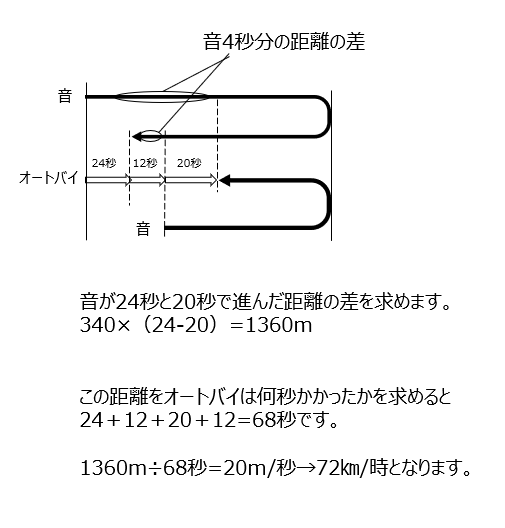
アプローチ⑦右1⃣
AB間の汽笛の問題です。時間がどの距離が何秒かかっているか、をキチンと押さえながら考えいきます。
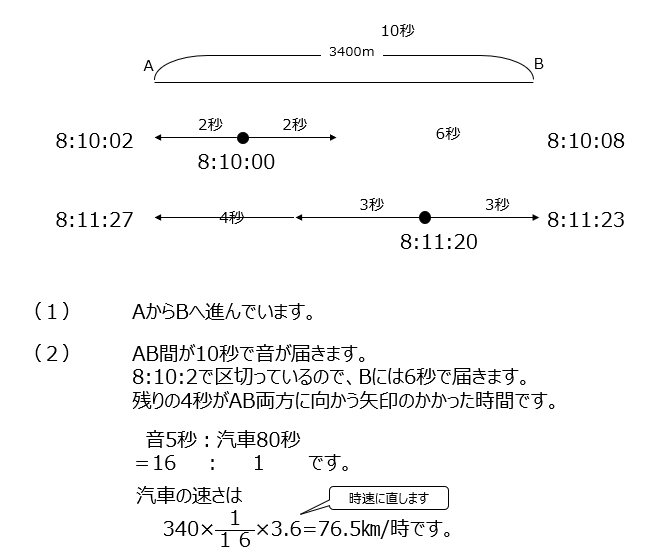
アプローチ⑧左1⃣
問題がややこしいですので、キチンと図に書いて進めましょう。動画での解説をお勧めしますね。
アプローチ⑧右1⃣
AとBとCで、どの同じ時間でどれとどれがどれだけ進んだか、をまとめないとなかなか解くのが難しい問題です。動画では色を変えて黒板で説明ありますので、なかなか分からない人は動画を見るようにしましょう。
実戦編A3⃣
距離を1、自転車の速さを1、予定でかかる時間も1として解いてみます。
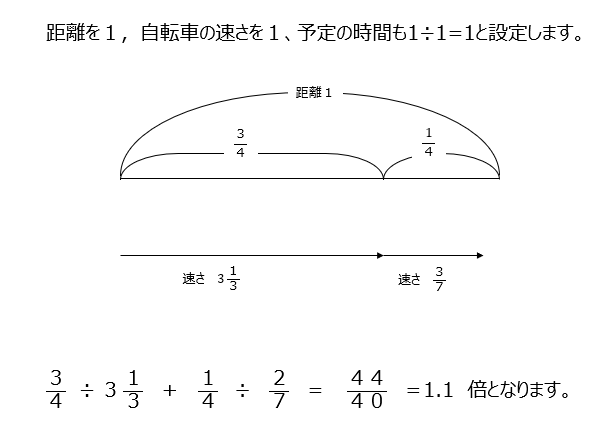
実戦編A4⃣
速さの比から逆比で時間の比、具体的な時間がわかれば速さの値がわかるので、流速も出ますね。流速が求まれば、次の問題はつるかめ算にて解けますね。

まとめ
速さの(1)でもありましたが、具体的な時間や距離が、比だといくらですか、を求めていく事で解き進めますよね。図に書き込む事で問題の理解が深まって回答に近づけるとおもいますので、頑張りましょう。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント