算数の動画「図形の移動」を見ました。
図形の式を書くことで理解は深まりますね、問題の図にもいろいろと書き込んで情報を整理しながら解きましょう。図形が移動した時に、どんな形になっているかのイメージが大切ですが、書いちゃえばいいと思います!

何秒後、とか、少し速さも出てきます・・・
導入と基本①2⃣
三角形を当てはめると、ちょうどおうぎ型になります。でも、図形の式を書いて、全体が三角形二つとおうぎ型で、そこから正方形を引く、という考え方を理解しておきましょう。また、よくある問題ですが、半径は与えられていなく、正方形の面積が与えられています。正方形の対角線が半径なのと、対角線×対角線÷2が面積なので、半径×半径は出てきますね。
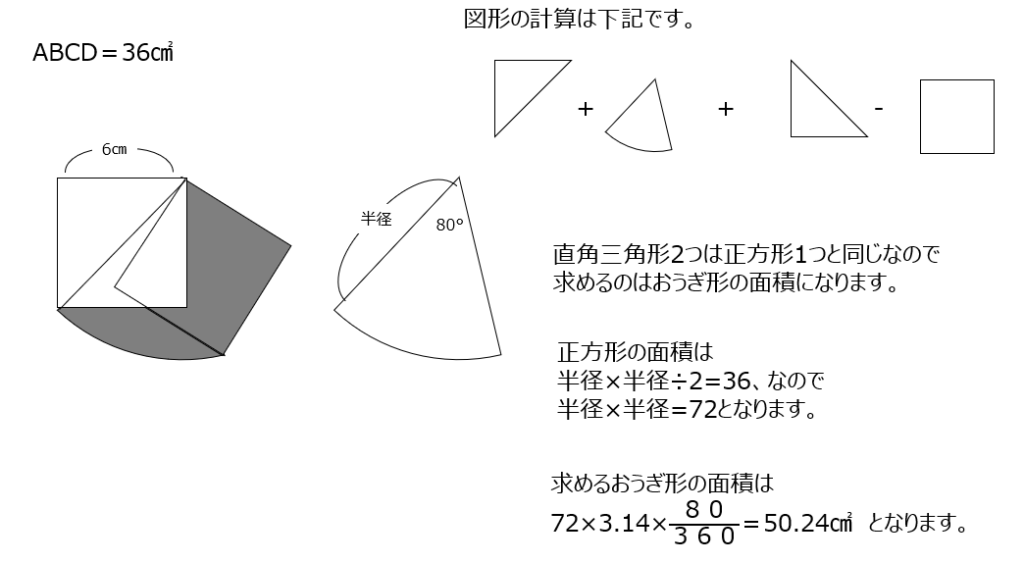
導入と基本②2⃣
図形の式を書くと、長方形+半円−半円、になるので、求めるのは長方形の面積になります。動画では斜線部の移動についても解説あります。
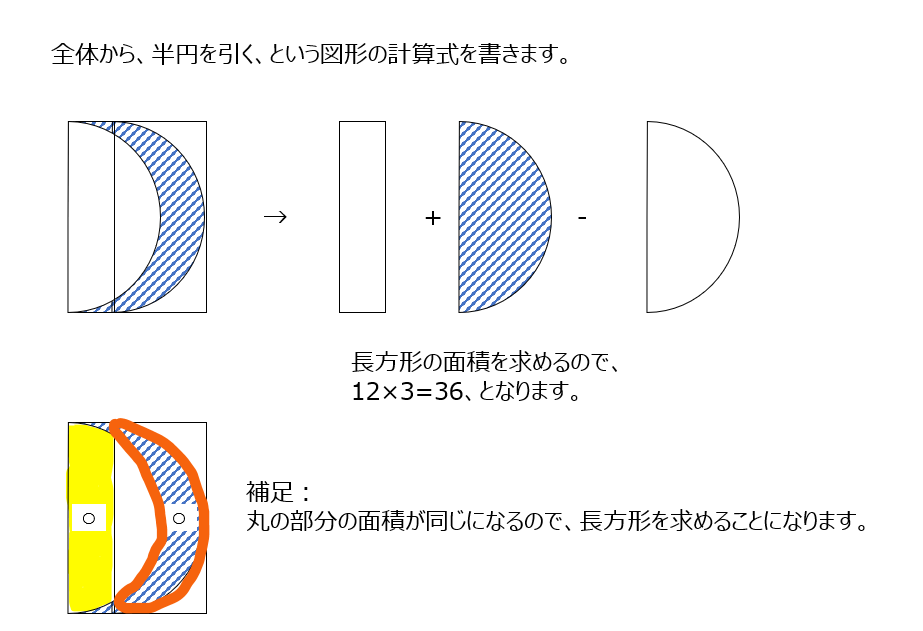
導入と基本②3⃣
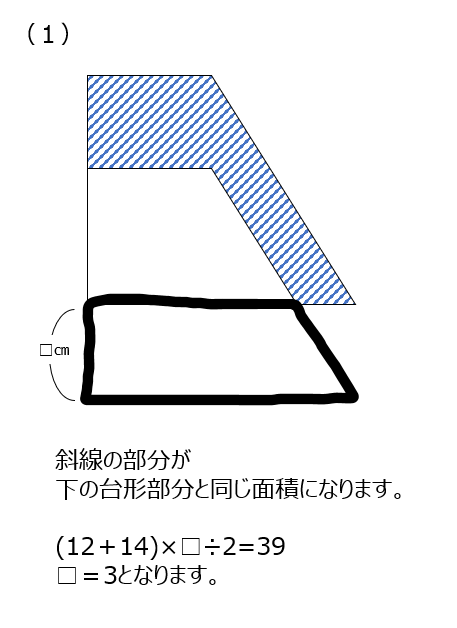
(1)台形を上にずらします。斜線部39㎠は台形の下の部分と同じです。
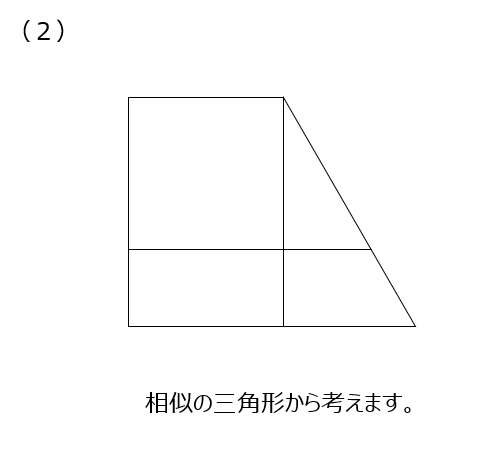
(2)Dから垂直に補助線を下に引きます、ピラミッド型の相似から解けます。
導入と基本③1⃣
平行四辺形を動かします、まずは1点を動かして考えます。点Cが動いた場合の図で説明があります。補足では、わかりやすく図形を動かす紹介もあります、今回は正方形を左に移動させるのもありですね。
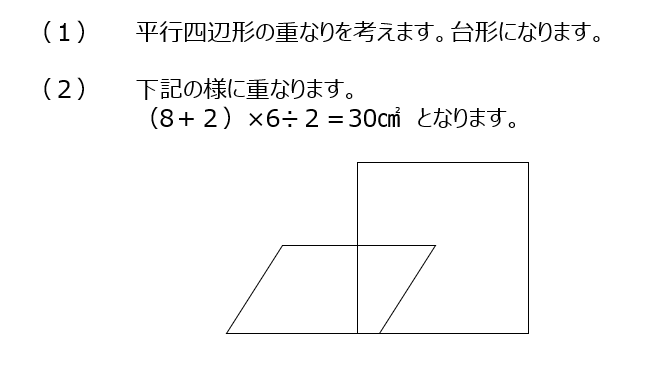
導入と基本③3⃣
2つの図形が向き合って近づきます。重なる面積が18㎠ということは、正方形だと一辺6cm、と考えると解きやすいですね。
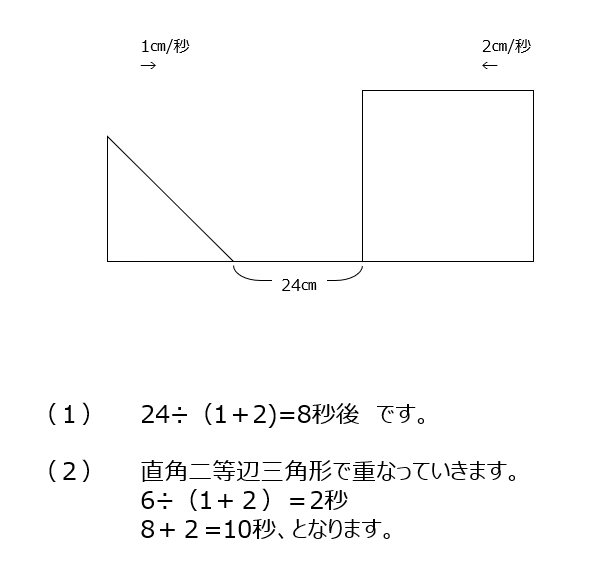
アプローチ①左1⃣
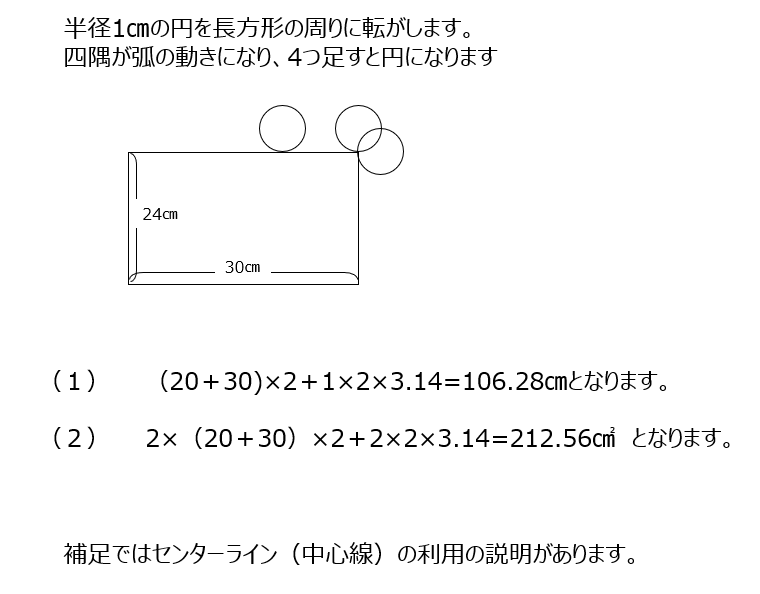
長方形の周りを円がまわります。その時の中心が動く距離や円の動いた面積を出します。補足では、センターライン(中心線)の利用、があります。動いた距離を2倍すると、動いた面積になります。理由は動画で確認しておきましょう。
アプローチ①右1⃣
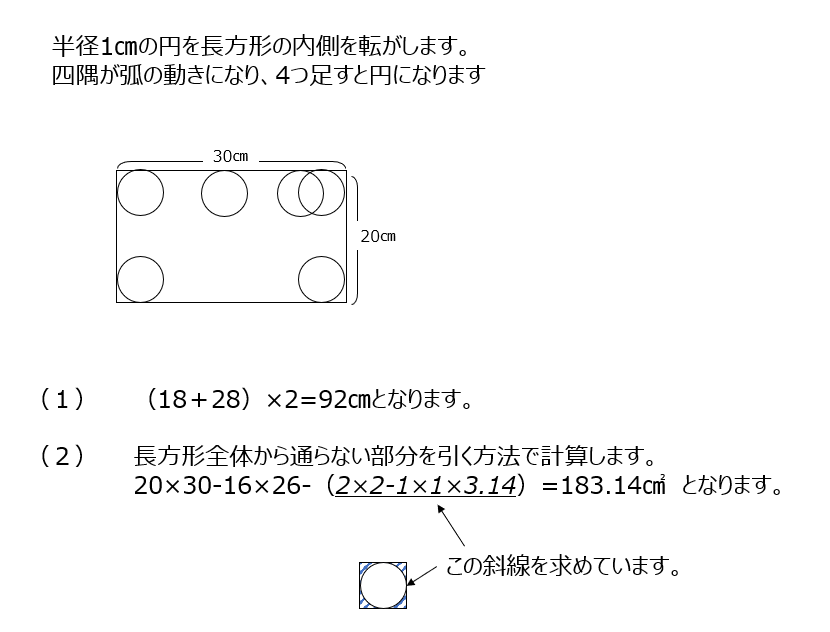
長方形の内側で円が動きます。四隅に円を書くと良いでしょう。全体の面積から、通っていない面積を引きます。
アプローチ②左1⃣
長方形の中を三角形が周りながら動きます。どの頂点がどう動いていくかをキチンと書いて、線で結びましょう。おうぎ型の動きをしていますよ。おうぎ型の中心角をまとめておいて、一度に計算しましょう!
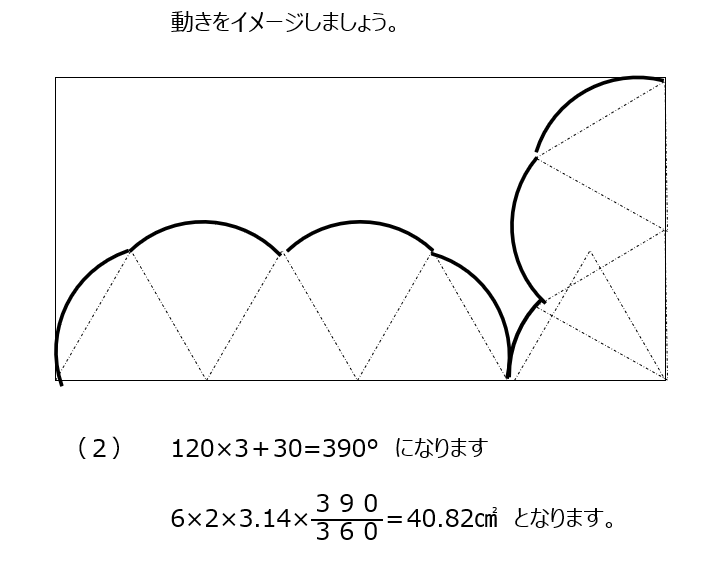
アプローチ②右1⃣
台形の周りを正三角形がまわります。キチンと動きを書けば、それほど難しくないかもですね、
アプローチ③左1⃣
おうぎ型が回転します。孤の部分で回転しているときは、直線で動きますので、確認しておきましょう。
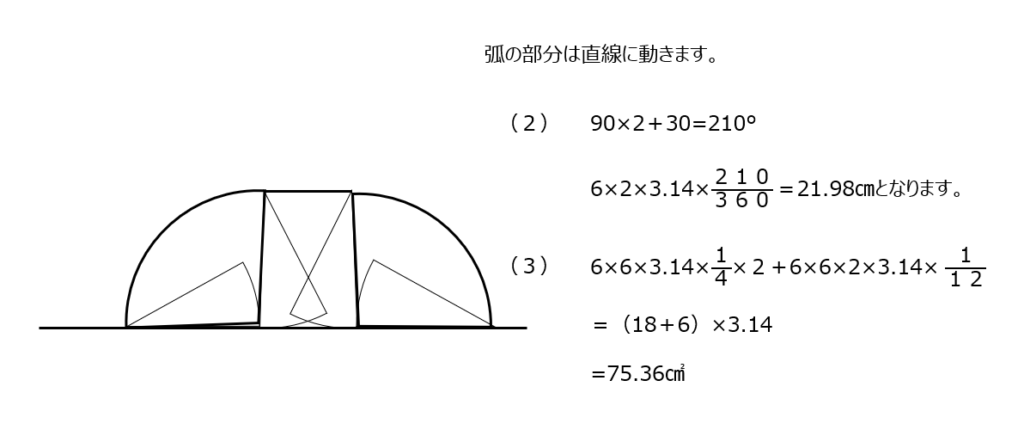
アプローチ③右1⃣
おうぎ型を回転させています。回転させた部分を自分で描いてみて考えます、おうぎ型から三角形を引いた部分の面積が同じ部分があります。(1)20×20×½=200㎠です。(2)200×3.14×(45÷360)で求まります。
実践編D2⃣
顔の描いた円がまわります、絵を描いてみると、顔が何回転したか分かります。(1)道が平な場合で1回転、道が丸くてBがすべって移動しても1回転するので合わせて2回転になります。次の問題も、1回転足すようにしましょう!
アプローチ④右2⃣
円周の周りを時計回りに回転する回数と、円の周りを時計回りに回転する1回を足します。反時計回りに回転するものは、円の周りを時計回りに回転する1回を引きます。
補足では、回転数の求め方の解説があります。1足すのか引くのか、ではなく、動く円の中心角点と、動く円周の中心と長さの比からでます。
式としては、中心が動いた長さ÷円周=回転数です。
アプローチ⑧1⃣
円周アの中心が動いた様子を考えます。動画では図示して丁寧に解説あります、是非、確認しましょう。先程の補足のやり方で解きます。4×2×円×½×3個、を2×2×円、でわると、3回転、とわかります。
アプローチ⑤2⃣
長方形と台形の重なりを考えます。(1)では重なりは三角形ですね(2)最大になるのは台形の時ですね。(3)重なりが台形全体の半分になる時ですが2回あります。
アプローチ⑥1⃣
動画では、黒板に全ての重なる時の図を書いてくれていますので、分からない場合は確認しておきましょう。重なりが1番大きい時も、図で書いて説明があります。移動する正方形を二等分する線は、必ず正方形の中心を通っていますよ。正方形の中心と平行四辺形が重なる点は2つあるので、その時を求めます。
アプローチ⑦左1⃣
おうぎ型がおうぎ型の周りを回ります。どう動くか、どこを中心に、どの線を線対称で動くか、などを、動画では加工しながら教えてくれますね、分かり易いです!もちろん、3.14の計算は最後にまとめてしますよ。
アプローチ⑦右1⃣
円が複雑な長方形の周りを周ります。中心の移動距離も、円の移動面積も、90度に曲がるところに注意ですね。丁寧に計算しましょう。
補足では、センターラインの利用があります。ただ、先程の90度に曲がるところの部分を引いてあげる必要があります。なかなか難しいですが、学習してモノにしたいですね。
まとめ
センターラインの考えなど知っていれば時短になりますね。多少の、イメージも大切ですが、キチンと図に書いて理解を深めたいですね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント