算数の動画「比と割合(1)」を見ました。
最も大切な単元、と言われてきた比と割合ですが、6年生の秋になってもう理解は出来てきたと思っています。理科でも普通に出てきますしね〜。復習している感じで授業中で理解してしまいましょう!

理科でも普通に使います、大事な単元ですよね
導入と基本③1⃣
50円玉4枚と100円玉7枚をひとつのセットで考えます。

アプローチ①左1⃣
どちらも問題文を式に書いて逆比を求めます。
(1)A:Bを逆比で求めます。
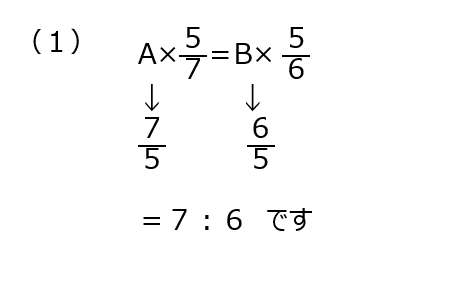
(2)3人の比でも、式に表して逆比にします。

アプローチ①右1⃣
食塩水の問題です。式を2つ書いて、消去算で求めます。次の問題では面積図で求めます。平均算ですね、丸と四角の比で動画説明ありますね。

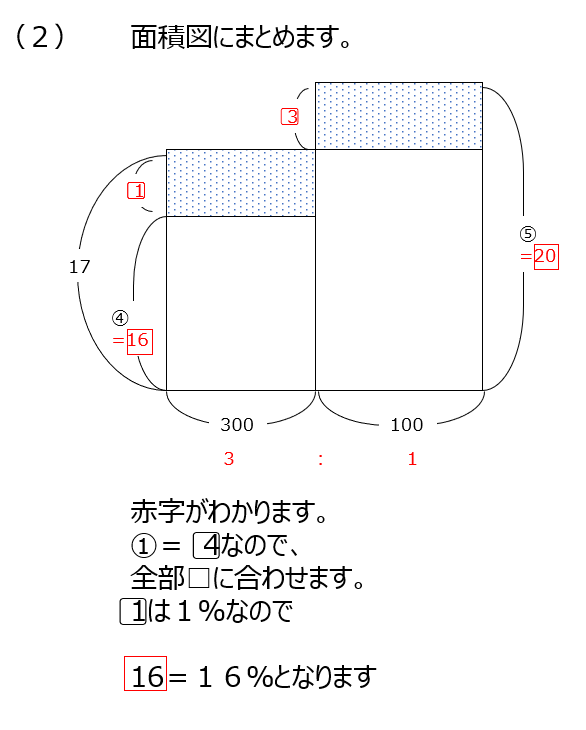
アプローチ②左1⃣
1aあたりの収穫量に畑の広さをかけると収穫高が分かります。AとBのそれぞれの比を書いていくと1aあたりの収穫量の比が分かりますので、そこから答えを求めます。
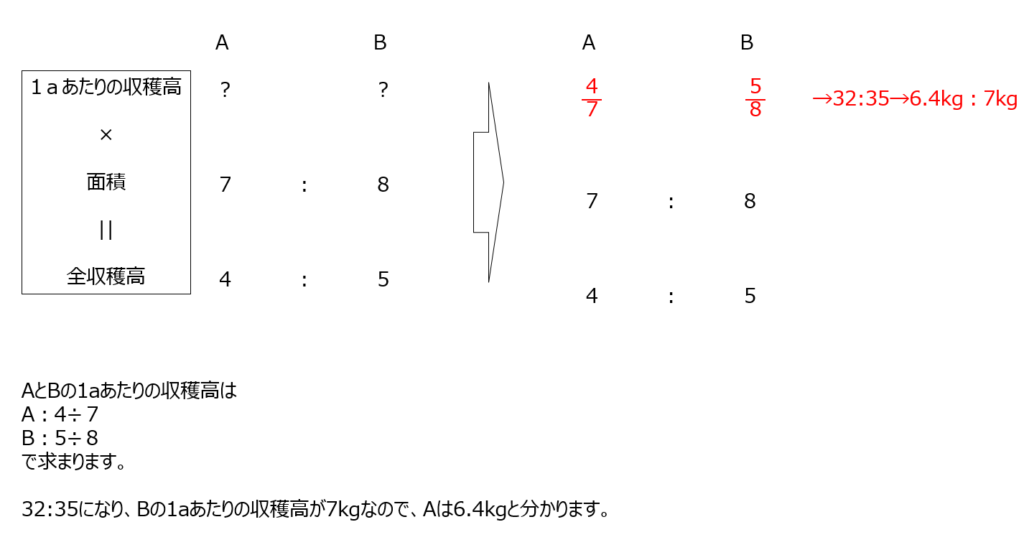
アプローチ②右1⃣
大人と子供の運賃の問題です。それぞれの運賃に、人数をかけて、全体の運賃を求めます。簡単な比にして解き進めます。
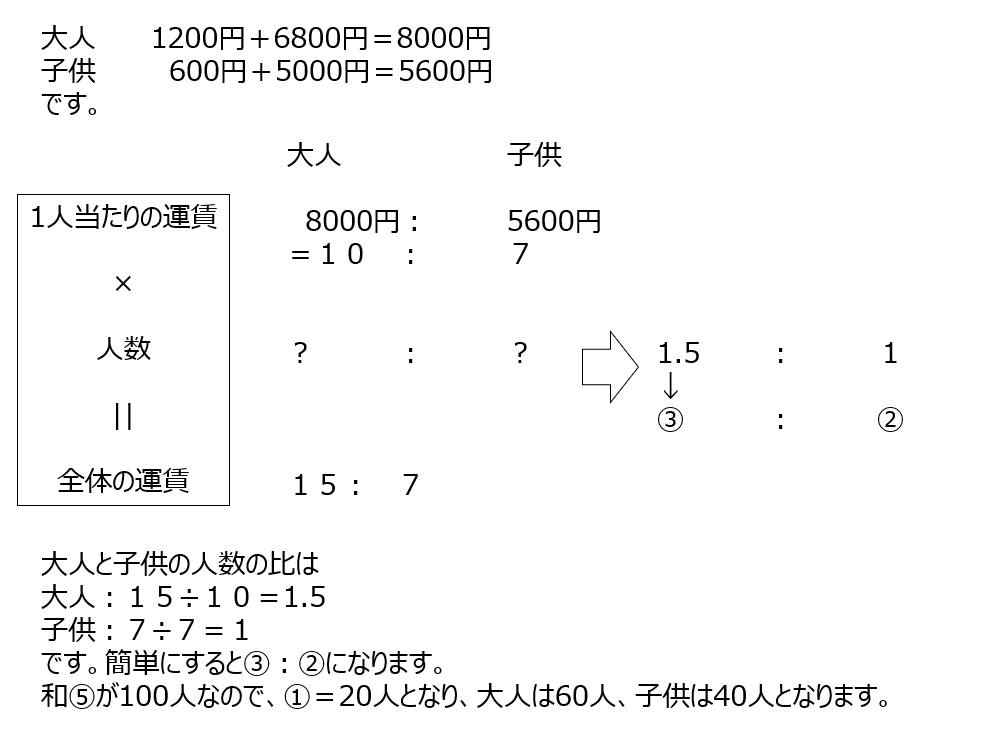
アプローチ③左1⃣
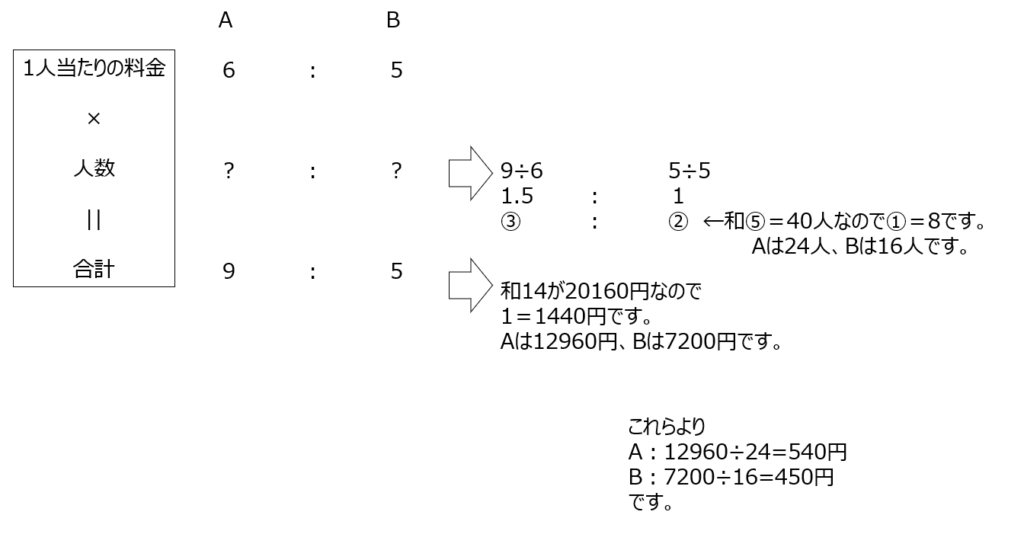
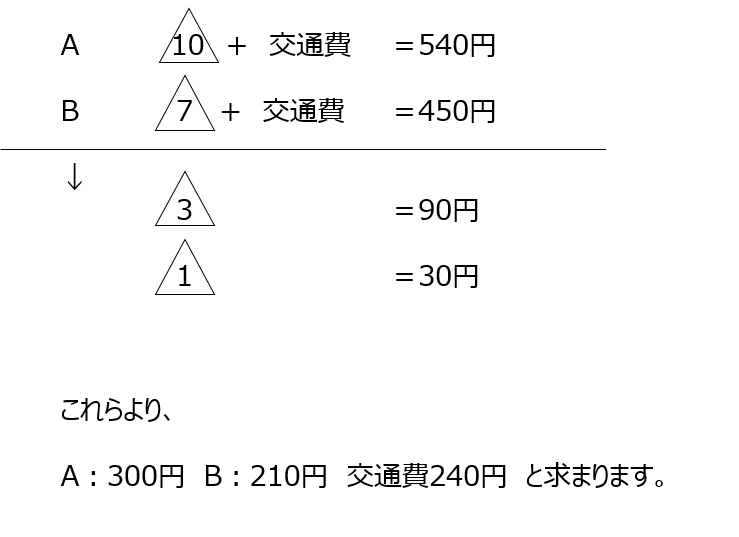
同様に、料金と人数で合計金額を出します。比は簡単な数値にしましょう。具体的な数のわかる人数の部分の比を求めます。合計金額も比で求まるので、それらから1人あたりの料金が分かります。最後は拝観料と交通費まで求めます、消去算です。
アプローチ③右1⃣
和差算で大玉と小玉の重さが分かります。ひとつの重さと個数と合計の重さの比から考えます。

アプローチ④左1⃣
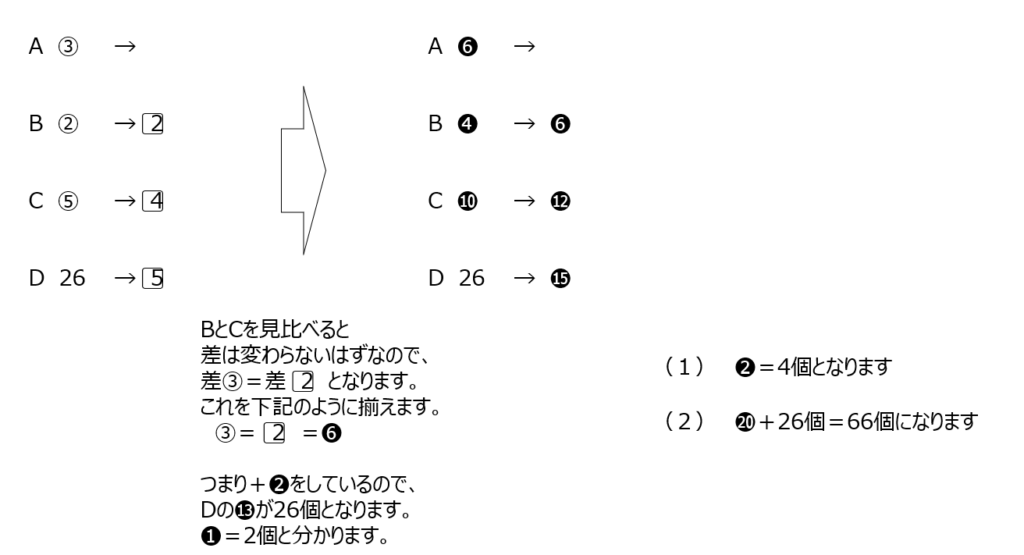
4つのお菓子の個数の比の問題です。BとCの個数の差は、変わらない事から、お菓子を増やす前後の比の差、も同じですね。お菓子を増やす前後の比を揃えれます。比を揃えれば、唯一、具体的は数値の分かるDで考えて解けます。
アプローチ④右1⃣
ノートの重さの比です。大を3g、小を2gとして考えます。消去算を使いますよ。

アプローチ⑤左1⃣
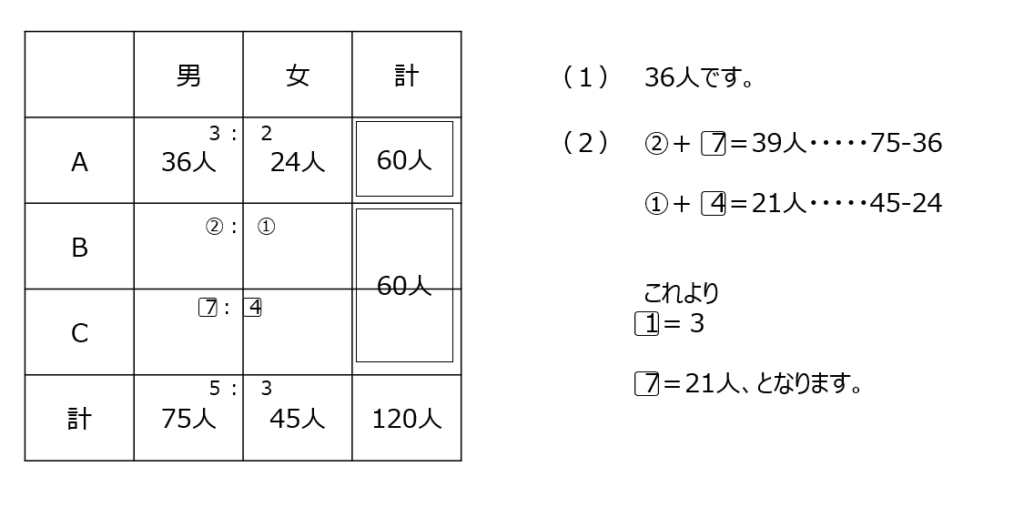
動画では、分かりやすく表にまとめて説明があります。全体の人数の条件から、Aグループの全体人数が分かります。BとCについては、男子と女子を合わせて考えて解きます。
アプローチ⑤右1⃣
切符と枚数の関係を整理します。4枚少ない、を取り除いて考える様にします。
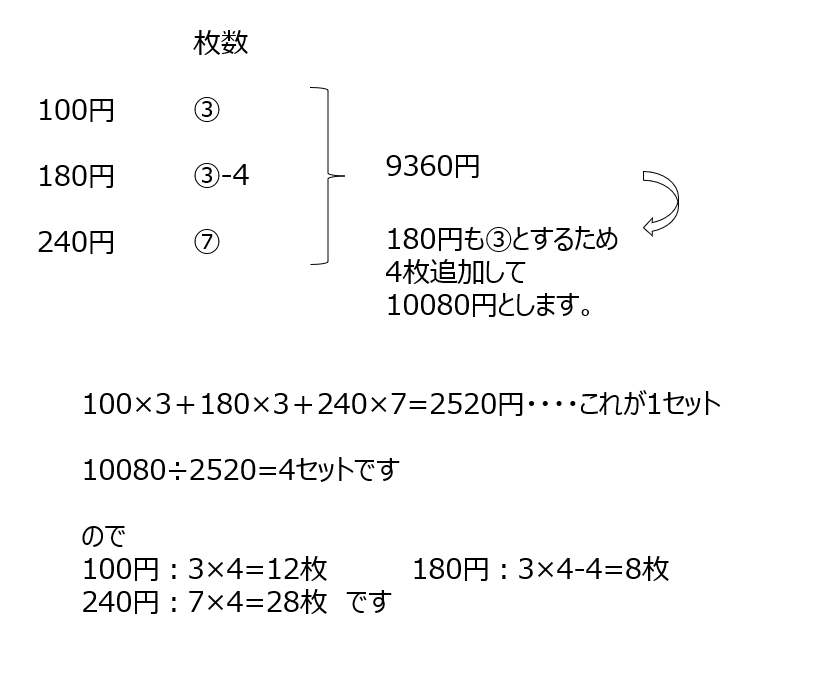
アプローチ⑥A1⃣
問題文をまずは式にまとめます。え、の条件から、CとAの比がわかるので、他の条件にわかった比を当てはめて考えます。Bの比もわかるので、全てが求まりますね。


アプローチ⑥B1⃣
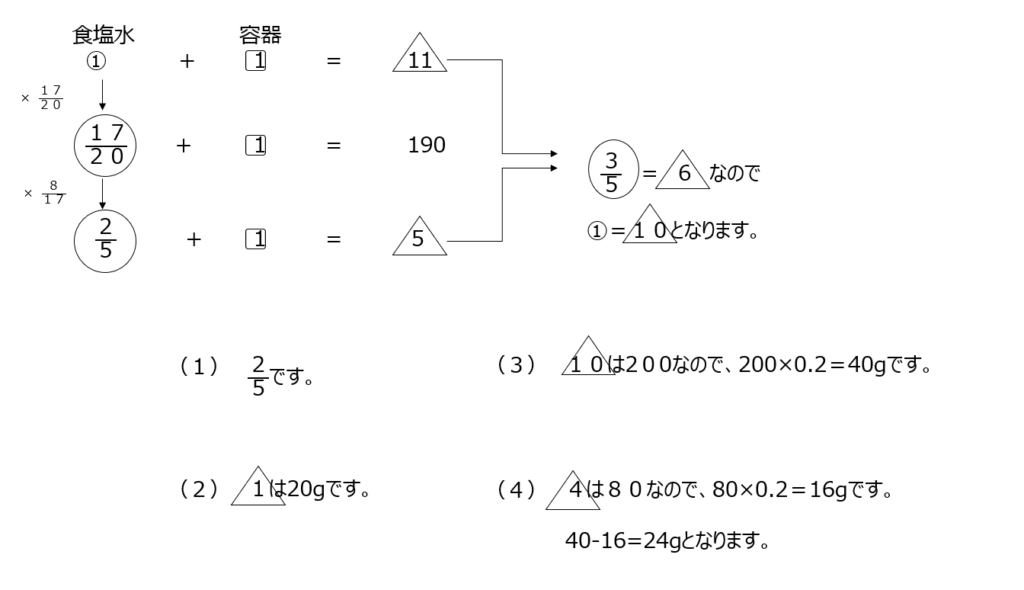
食塩水と容器と全体の重さの問題です。変わっていく食塩水の重さをキチンと理解して比で表していきます。最後の沈殿した食塩を水に変えるのは、重さは変わらない、という事です。全体の重さの比の差や、食塩水の比の差などから、お互いの異なる比を揃えることができます。
実戦編B4⃣
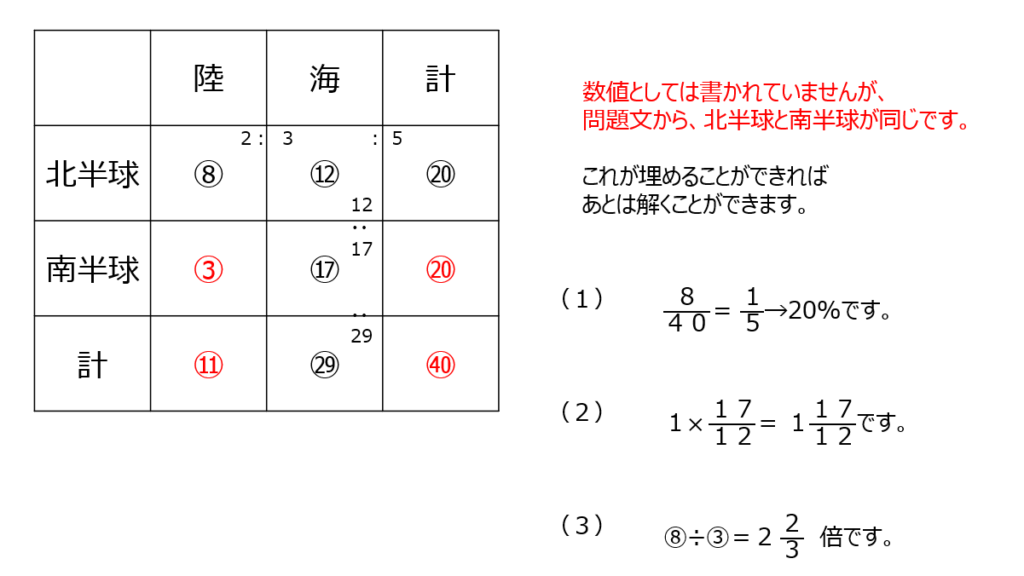
陸と海と、北半球と南半球の、比の割合を、表にまとめて考えます。比を揃えて考えましょう。問題文には数値としては書かれていませんが、北半球の陸と海の合計は、南半球の陸と海の合計と同じですね、読み取れましたか?
実戦編E2⃣
問題文かややこしいですが、図示します。どれを1とするか、ですが、動画ではCを1として解説があります。あとは式にして解き進めます。
アプローチ⑧1⃣
立体の切断です。切り口が表面に表れてくる所はまずは書いてしまいましょう。切り口を延ばして考えます。体積を三角錐のはみ出た小さいものを引く考え方です。辺の比を三回かけると体積の比になりますよね。
今週の立体切断1⃣
積み木で作ったような立方体を切ります、動画では各断面を一つずつ説明があります。切られた積み木の数を各段で説明がありますね。全く切られていない積み木、も、各段の図から数えて求める事ができます。最後に各段で図示せずにまとめて考える方法も教えてくれますが、切られない立方体の数を数えるのは煩雑になるので、頭の中で、各段のイメージも持つようにしましょう。
まとめ
問題文の図示化が出来てしまえは、半分は解けたようなものですね、それくらい大事ですね。分かりやすく書くテクニック、も必要ですが、問題文の読み取る国語力ですね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント