算数の動画「速さ(2)」を見ました。
時計算、通過算、流水算、とたくさん速さ関連の問題を習ってきましたが、比を交えた問題となり、集大成ですね!復習、という位置づけで、平常授業をこなしてもらいたいものです。わからない問題でも、図に書いていけば何とか解けるようになる、、とおもいますよ!

基本を駆使して解き進めれますよ!
導入と基本②1⃣
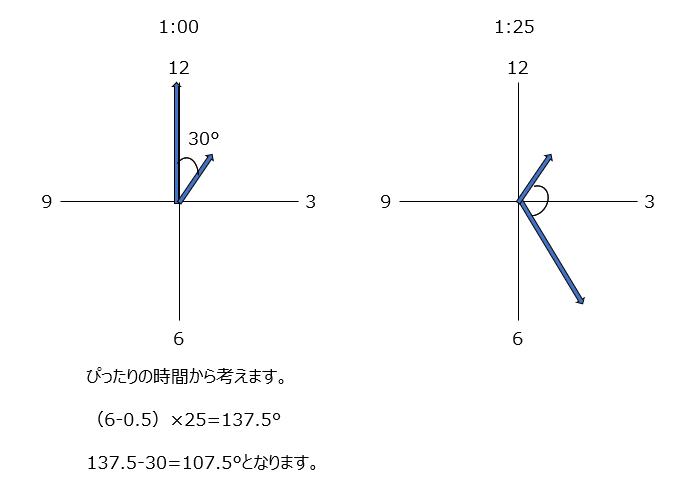
時計算の再確認です。1分間で長針は短針より5.5度動きます。1:00から考えて、25分後の差、と、1時の時の差、を引き算します。
導入と基本②4⃣
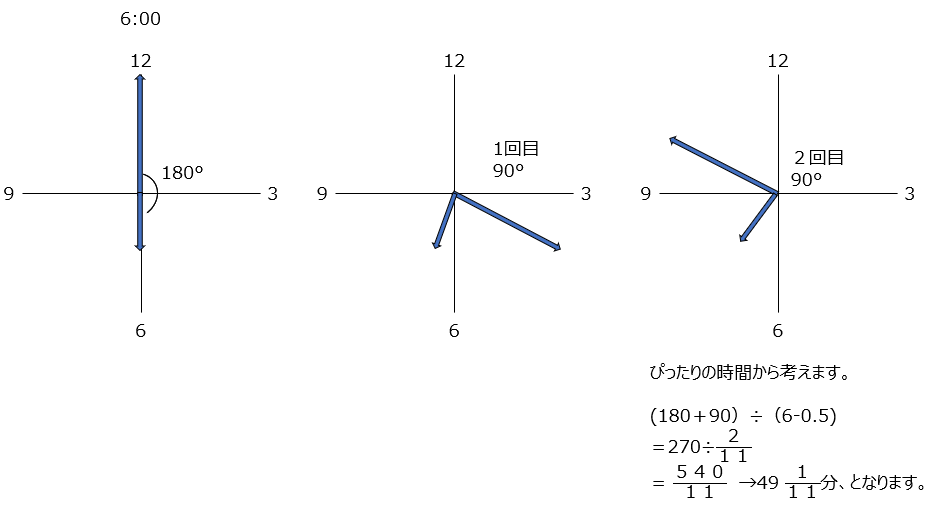
6時と7時の間で2回目の直角になる時刻、を求めます。6時ちょうどの図から書いてみましょう。長針が短針より270度多く進みます。分数での答えとなりますよ。
アプローチ①1⃣
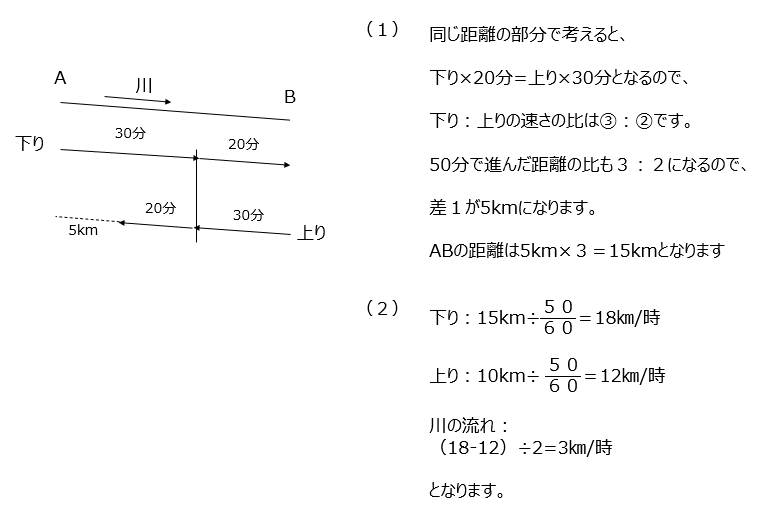
流水算です。図に書いてまとめて解き進めましょう。図に書くと、同じ距離でかかった時間が上りと下りでわかるので、上りと下りの速さの比がわかります。速さの比は、進んだ距離の比、を使用します。
アプローチ①右1⃣
通過算です。解法1では、急行がかかった時間を、もし普通の場合は、として考えます。速さがの逆比になりますね。普通が200mの鉄橋でかかった式と計算して解きます。解法2では、普通と急行の鉄橋でかかった比がわかるので、そこから求めます。単位に気を付けましょう!


アプローチ②左1⃣
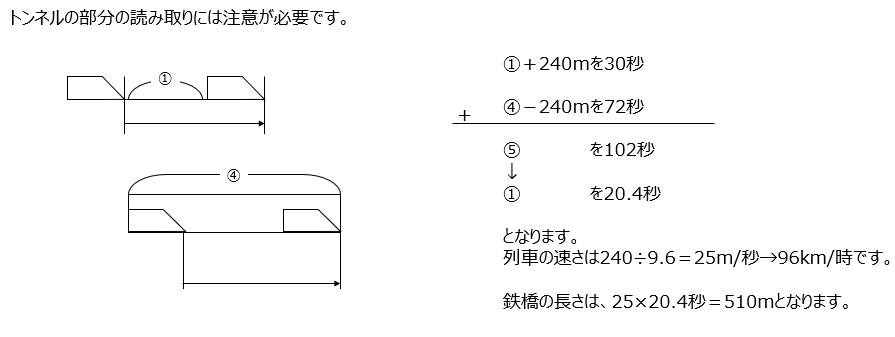
トンネルの隠れている状況は、列車の後ろがトンネルに入って、先頭がトンネルにかかった時、なので、距離はトンネルから列車の長さを引いたものになります。消去算は気を付けて計算しましょう。
アプローチ②右1⃣
時速を秒速に直して考えましょう。問題文を急行、特急、ホームの長さ、を整理してまとめていきます。動画では、各長さをまとめて計算している図の説明がわかりやすくあります。

アプローチ③左1⃣
通過算です、図にまとめて解いていきましょう。問題文から式が2つできますので、その式からA君の速さがわかります。
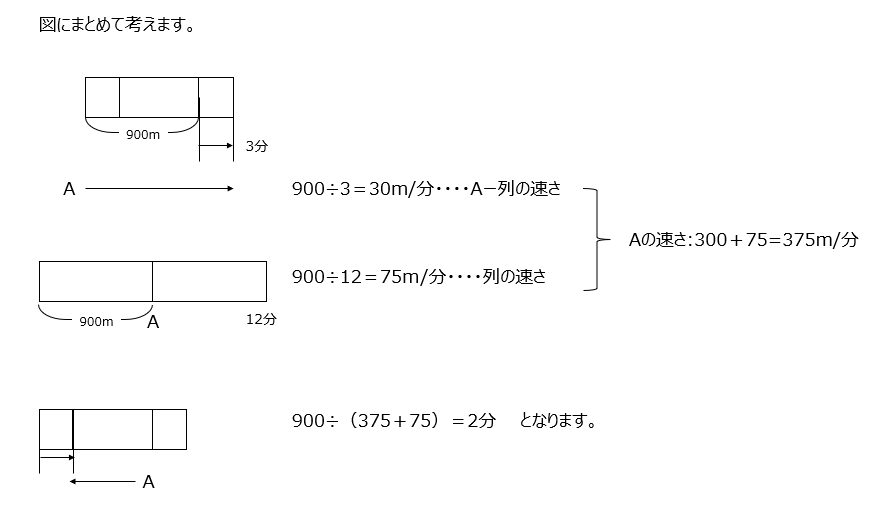
アプローチ③右1⃣
通過算です、先生の速さと列の速さの、和なのか、差なのか、式を2つ作れます。2つの式から、割る数の比がわかるので、そこの違いから計算して求めます。このやり方は以前からも出てきていますので、得意じゃない場合は、動画を確認しましょう。

アプローチ④1⃣
時計算です、問題の意味が分かりずらいですが、読み解きましょう。3時から4時の間の問題なので、長針はおおよそ7くらいの位置、として考えて図を書いてみます。追いかけっこ(旅人算)として考えるのはむつかしいです。図に比を書いて考えていくと、90度の部分の比がわかります。動画がわかりやすいですね。
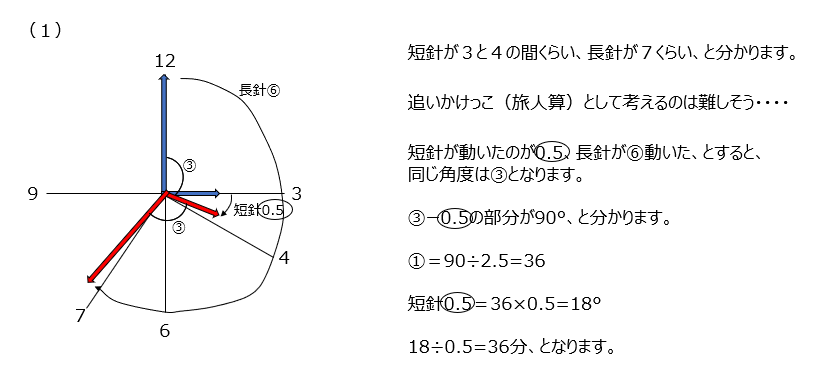
別の考え方で、少し難しいですが、追いかけっこ(旅人算)で解けるか、考えます。「長針の半分の速さの針が、短針に追いつく問題」として考えることができます。

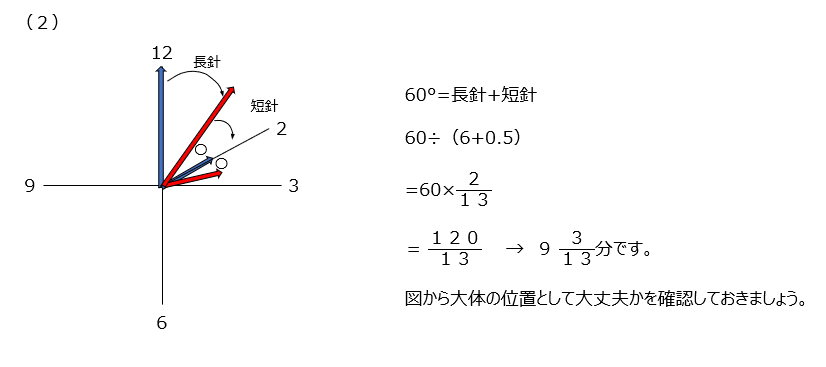
(2)では2時と3時の間で、2を中心に等しい角度の時間、を求めます。長針と短針の進んだ和が60度、として考えます。
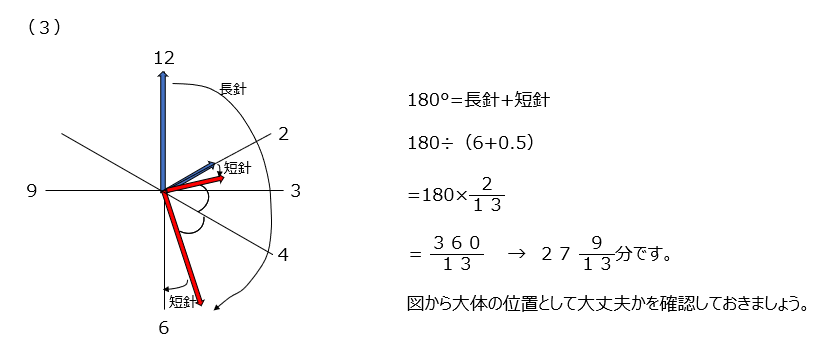
(3) では2時と3時の間で、4を中心に等しい角度の時間、を求めます 。 長針と短針の進んだ和が180度、として考えます。 角度の扱いは動画で確認しましょう。
アプローチ⑤A1⃣
動く歩道の問題です。歩数で距離を求めます。(2)の解法1では、父が動く歩道に乗った歩数から、動く歩道が進んだ距離が歩数で分かります。解法2では歩数の比は、時間の比になることも用いて解きます。聖くんとお父さんと動く歩道、で速さと時間の比を使って解きます。

アプローチ⑤B左1⃣
太郎と次郎とエスカレータの問題です。解法1では、太郎とエスカレータの速さの比がでます、次郎の場合はエスカレータの速さは同じなので、そこから考えます。解法2では進んだ段数と時間の比が同じなので、速さの比は逆比となり、そこから解き進めます。
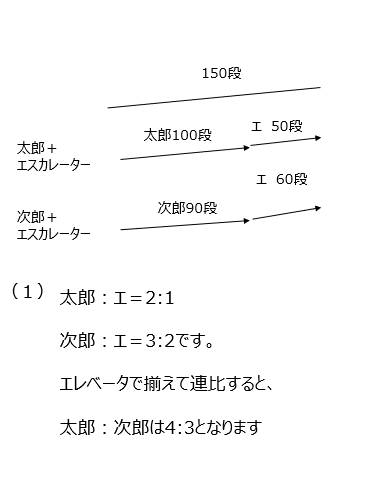
アプローチ⑤B右1⃣
流水算です。問題文を動画では丁寧に図に記載して説明してくれています。モーターボートと船の問題です。船の速さがわかるので、モーターボートの進んだ距離がわかります。
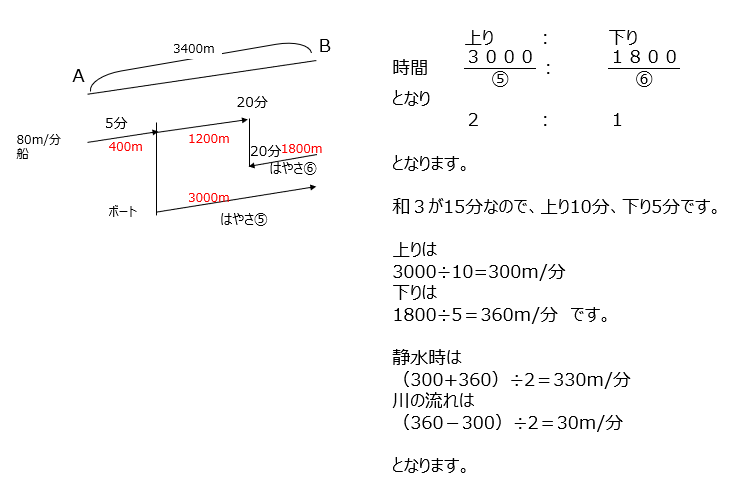
アプローチ⑥1⃣
通過算です。特急と急行の時間の比から速さを求めます。図に書いて解きましょう!なかなかむつかしいですね。
実践編A3⃣
時計算です。最初の長針と短針の差、から、100°開くのは2回あります。それぞれの時間を求めるのではなく、その2回の差は200°なので、それを速さの差で割ることで簡単に求まります。
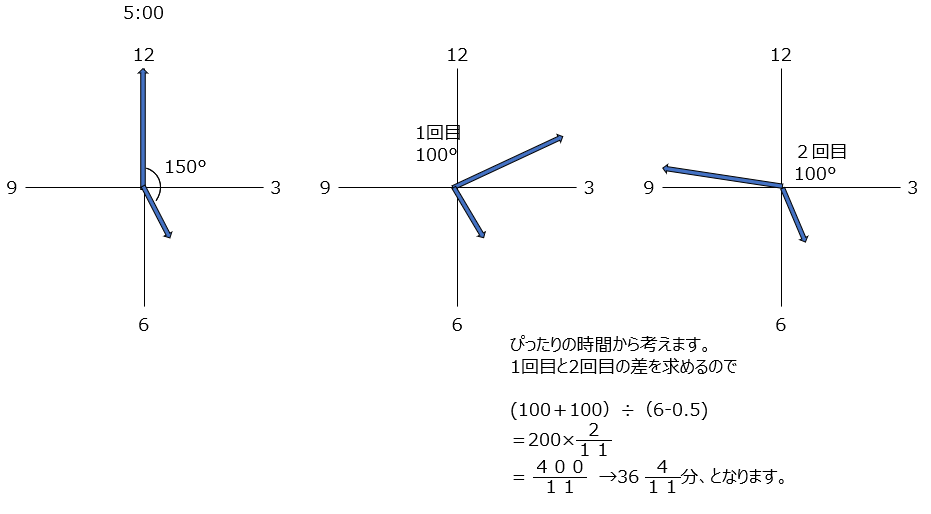
実践編B1⃣
5直角、は90°×5、のことです。午前、午後、で答えを聞かれている場合は気を付けて答えましょう。

実践編B2⃣
動く歩道の問題です。同じ距離を進んだ時の時間に着目して解きます。この問題も分速と秒、で単位を気を付けましょう。
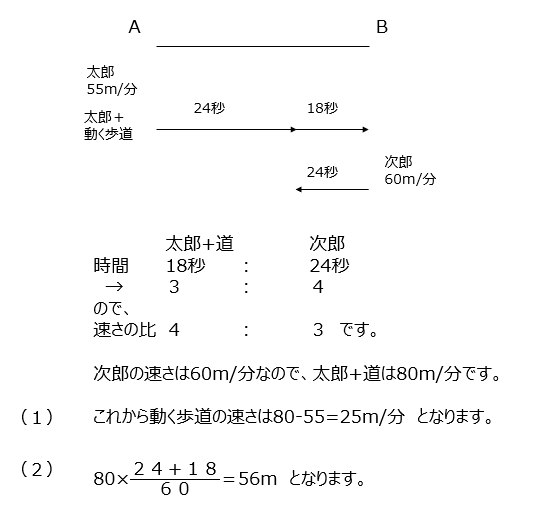
アプローチ⑧1⃣
小立方体がいくつ切られるか、の問題です。各段でいくつ切れるか、を丁寧に説明して頂いていて、その後にまとめて考えて書く方法の紹介になります。
アプローチ⑧2⃣
先ほどの問題を、1つの図でまとめて考える方法の解き方を説明してくれています。今まで何度か出てきた解法です、身についているかどうか、再確認しましょう。
今週の立体切断1⃣
小立方体を切る今まで実施してきた問題と同じですね、同じやり方で解けますね。この問題では真ん中が無い問題です。体積は一段ずつ考えて進めてみましょう!
まとめ
速さの問題ですが、同じ距離を進んだ時間に着目する問題が多かったですね。時間の比から、速さは逆比にして、、、とお決まりの解き方とはいえ、図に書いての理解が大切ですので、わからない問題でも図に書いて解き進めるようにしないといけませんね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント