算数の動画「平面図形(1)」を見ました。
補助線を引くセンス、ってどうやって身に着けるんでしょうね、これは訓練である程度は賄えるとおもいます。たくさんの問題に触れて経験値を積んでいきましょう!

練習あるのみですよ!
導入と基本①4⃣
真ん中の三角形から両端の小さな三角形を引きます。
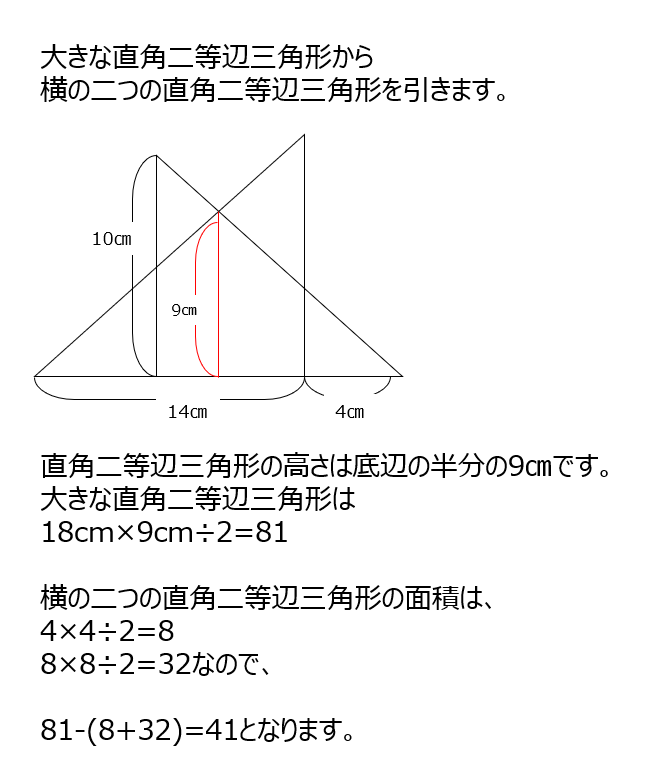
アプローチ①左1⃣
影の長さの問題です。平行線を補助線として引いて、相似の三角形から解きます。
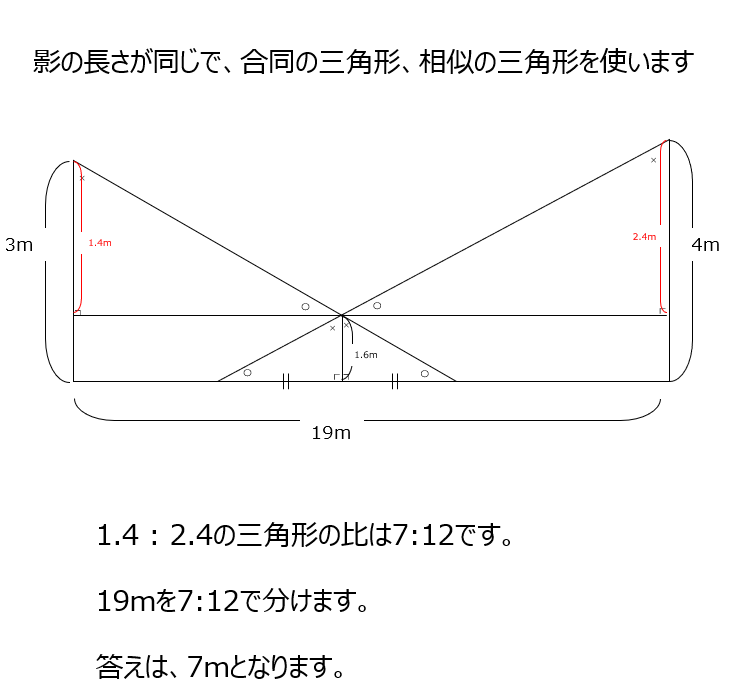
アプローチ①右1⃣
側面の三角形の相似から着目して解きます。(3)は解法1では、全体から前面の図形のよう体積を引きます。前面の立体を、三角柱と三角錐に分けて考えます。解法2では、断頭三角柱を使って直接求めます。


アプローチ②左1⃣
影の問題ですが、立体ではなく平面図で考えます。横から見た時の平面図を書いて、三角形の相似を見つけます。動画では丁寧な図の説明がありますよ。
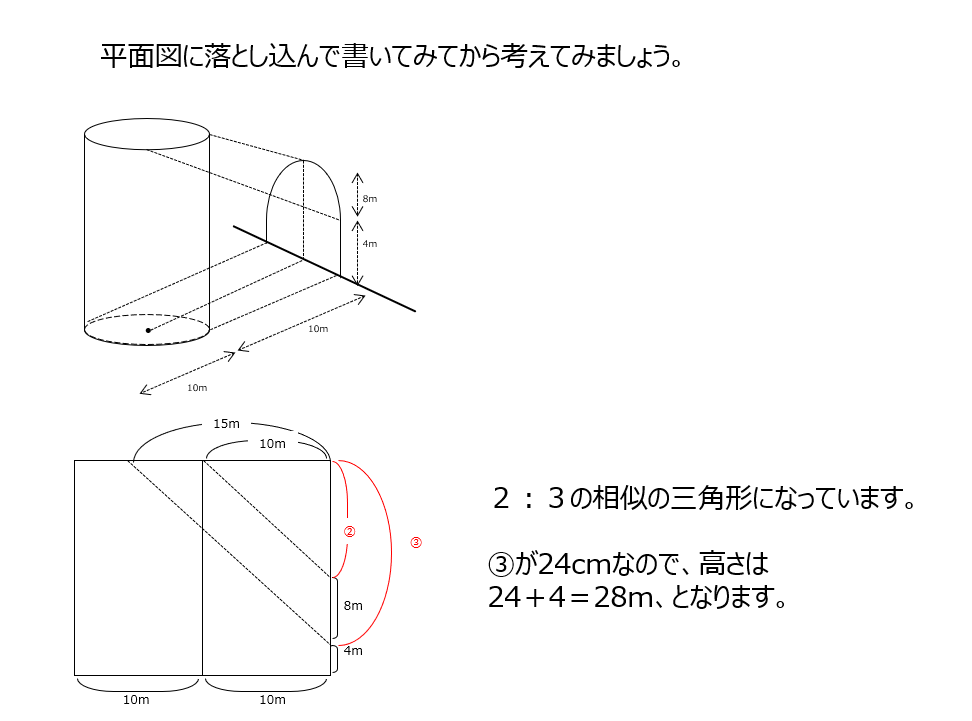
アプローチ②右1⃣
長さが同じ図形と比の問題です、二等辺三角形で考えます。同じ長さの部分以外を比で表して、上の二等辺三角形の一辺が分かります。あとは相似を用いて面積を出します。
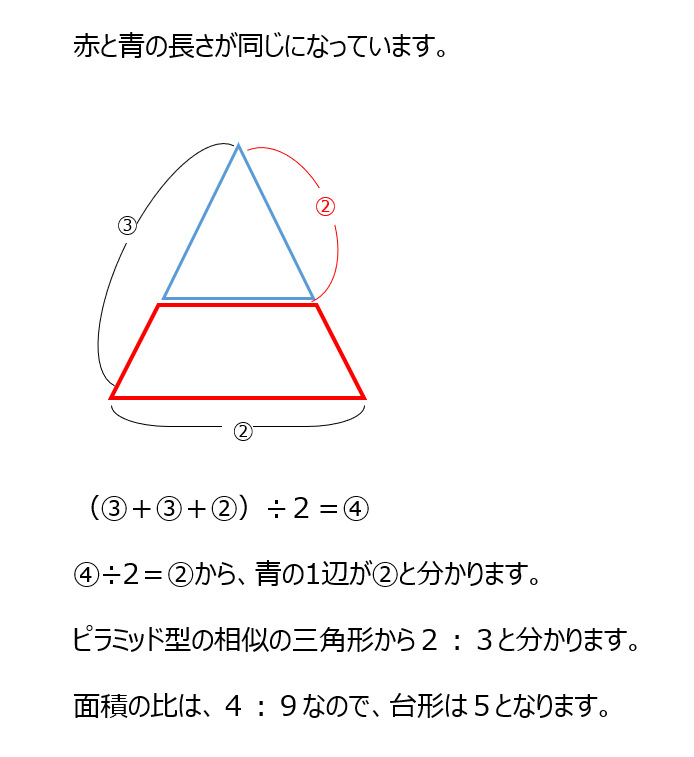
アプローチ③左1⃣
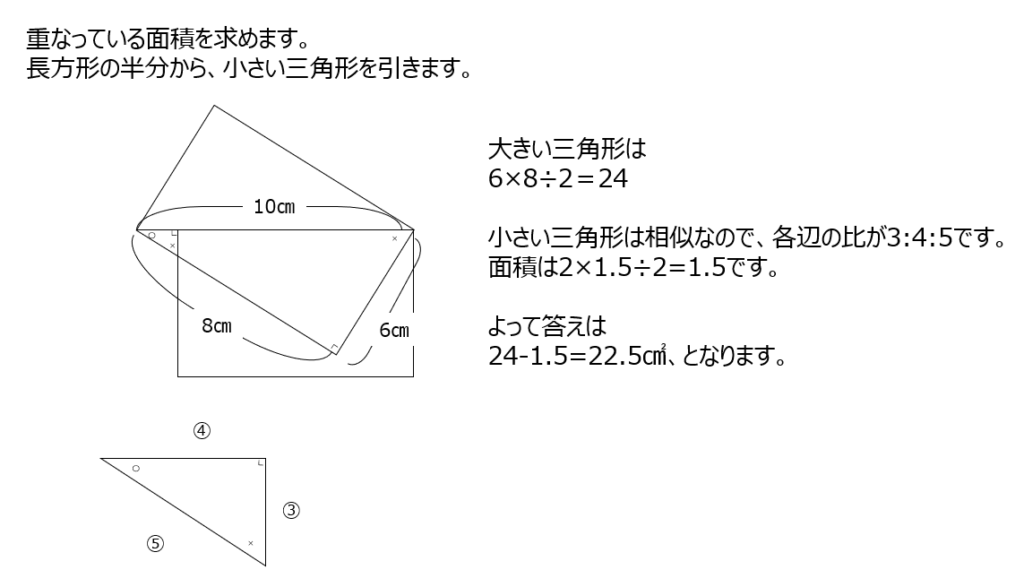
斜線の面積を求めます。大きい三角形から、小さい三角形を引くイメージです。大きい三角形と小さい三角形は角度が三つとも同じなので相似です。
アプローチ③右1⃣
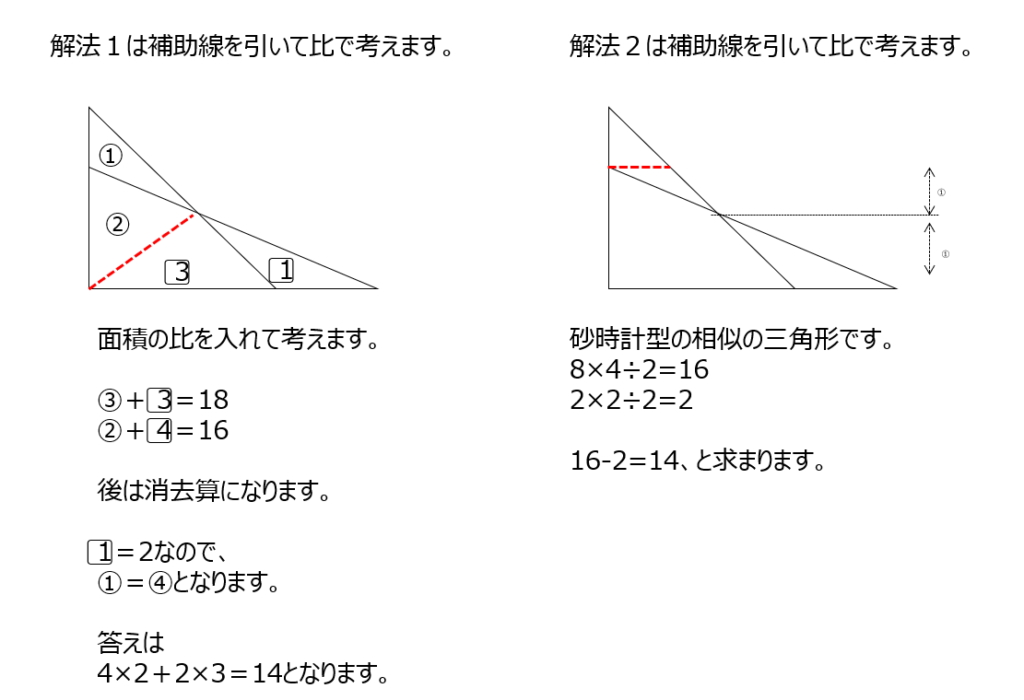
斜線の面積を求めます。解法1では、斜線部を二つに分けて、高さが同じ三角形の底辺の長さの比から、面積比を二つ出して消去算します。解法2では、平行線を引いて砂時計型の相似を用いて解きます。
アプローチ④右1⃣
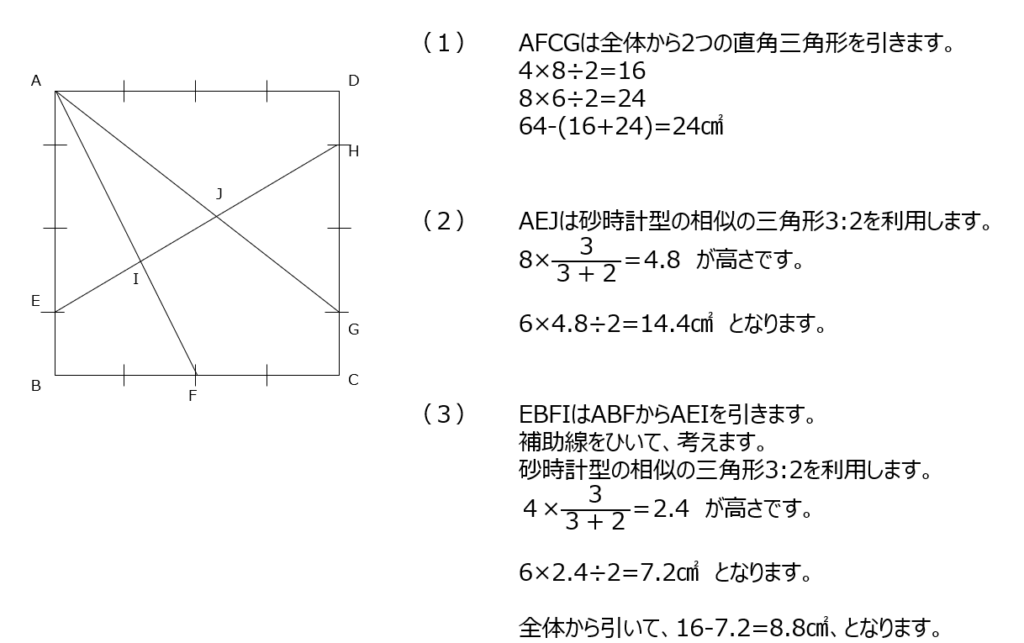
(1)では、全体から二つの三角形を引いて求めます。(2)では、砂時計型の相似から、高さを求めます。(3)では点Fから上に補助線を引いて、砂時計型の相似を用いて、全体から引いて解きます。
アプローチ⑤左1⃣
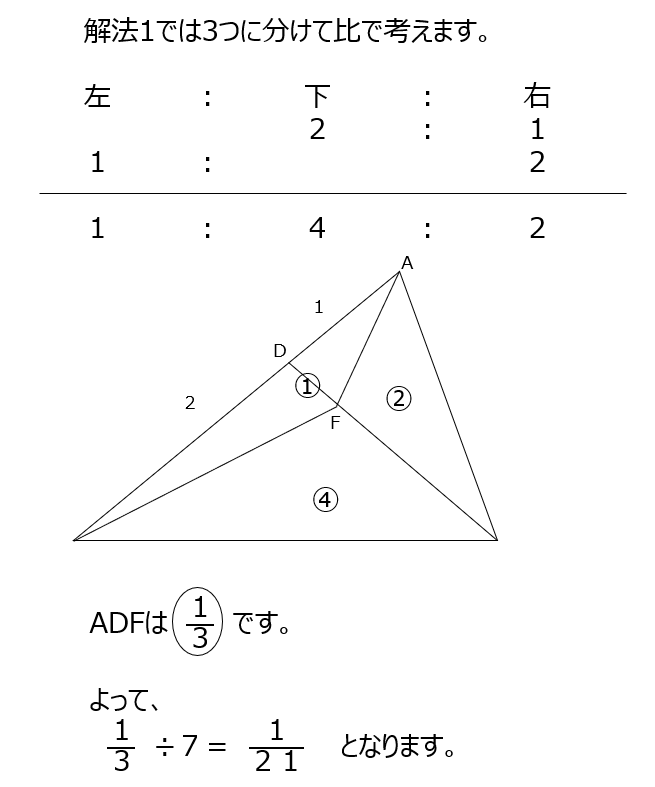
解法1では、BFを引いて伸ばして3つに分けて考えます。3つの三角形の底辺の長さから、面積比を求めて解きます。解法2では、Dから底辺に平行な補助線を引いて、ピラミッド型と砂時計型の相似の三角形を用います。
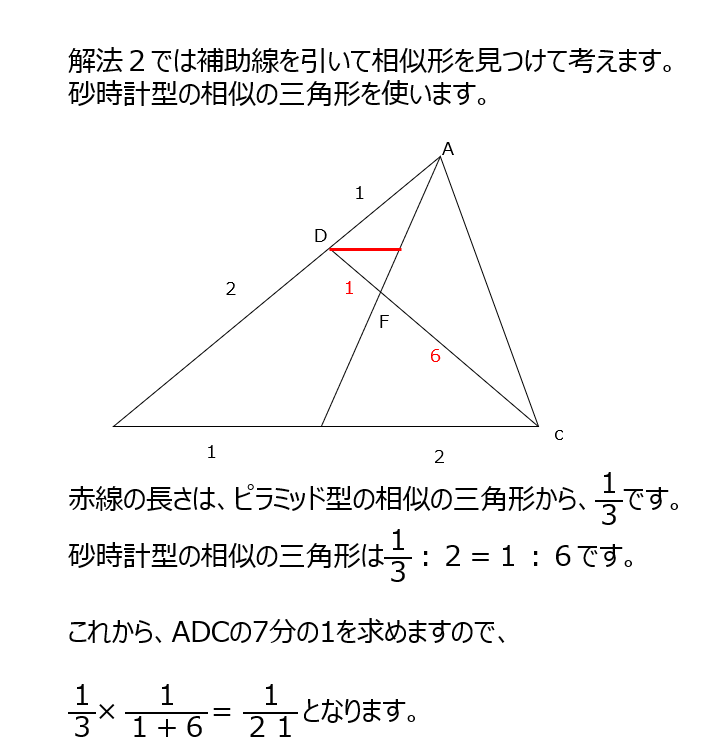
アプローチ⑤右1⃣
補助線を引いて3つの三角形の面積比を出します。動画では各三角形に色をつけて説明してくれていて分かりやすいですね。
アプローチ⑥1⃣
動画では板にできる影の様子を書き込んで説明しています。横から見た図の説明もわかりやすいですね。影ができる時の三角形の比を用いて、影の四角形の高さを求めます。
実践編B1⃣
400分の1から戻して、500分の1にして計算し直します。

実践編B3⃣
長方形と二等辺三角形の面積が同じ、で、底辺が同じなので、高さのに比が2倍になります。砂時計型の相似から、長さの比が分かります。
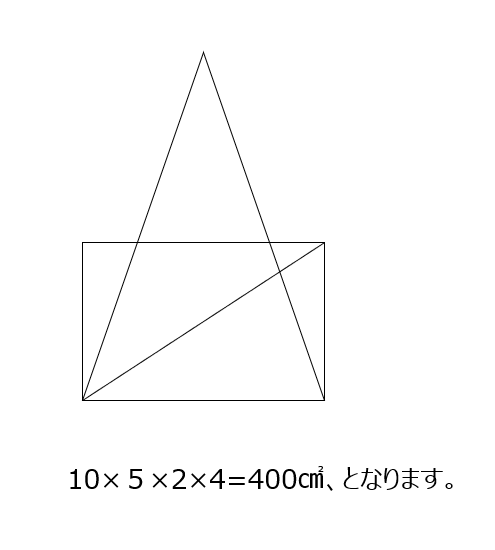
実践編C3⃣
よくある図形ですので解けるようになりましょう!ピラミッド型の相似から、各辺の比を求めます。真ん中の平行四辺形は全体の3分の1ですよ。

実践編D1⃣
正三角形の半分の三角形なので、長さの比が1:2になります。
アプローチ⑧1⃣
立体体を積み上げた立体体を切断する問題です。残る体積が2種類あるのでその数を数えて計算します。どちら側が切られるか、で残る体積が変わってきます。
今週の立体切断
各段に分けて、線を引いて考えるようにします。なかなかイメージつかない人は動画での確認をお勧めします。
まとめ
基本的な考え方は、相似を用いて、ピラミッド型や砂時計型を見つけて解いていく、というのは変わりません。見つからなかったら自分で補助線引いて作ってしましましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント