算数の動画「立体図形(3)」見ました。
母線の考え方は新しいですけど、動画では丁寧に説明があります。しっかりと身につけましょう。次のマンスリー目指して、気を取り直して始めましょう!

立体図形は僕も苦手かも、、、一緒に学びましょう!
全体のまとめ
体積、表面積を求めます。
回転させるので、3.14の掛け算が出てきます。
3.14の掛け算は面倒なので、1回で済むように計算を工夫していくことが大事ですね。
まずは、式を書いて、そこから計算を工夫する、が、当たり前な話ですが、効率的なようです。
特に表面積は、式を全部書ききってから計算しましょう。
◆基礎◆標準
アプローチ①左1⃣
柱体の体積の求め方は、底面積×高さ、です。これを用いて解きます。(1)底面積は直角三角形です。(2)底面積は円です。(3)底面積は半円です、計算を楽にするために分数で解きましょう。
アプローチ①右1⃣
表面積はすべての面積を求めます。側面の面積は、底面積の周りの長さに高さを掛けて求めるようにします。(1)直角三角形を底面積として考えます。(2)円を底面積として計算します、3.14の計算は最後に一度だけするように敬さんお工夫をします。(3)半円を底面積とします。3.14の計算は最後にまとめてします。
アプローチ②左1⃣
・すい体の体積=底面積×高さ×1/3
・側面(おうぎ形)の弧=底面の円周
(1)底面積が四角形で考えます、四角すいです。(2)底面積を直角三角形とします、三角すいです。(3)円すいです。
アプローチ②右1⃣
四角すいの見取り図を描いてみます。底面を書いて底面の真ん中(対角線の交点)から垂直に伸ばすと書けます。体積は、底面積(10×10)に高さ12を掛けて、3で割ります。表面では、側面の二等辺三角形の高さが13cmなので、10×13/1/2が4つある、と考えることができます。
アプローチ③左1⃣
円すいの展開図と見取り図があります。円すいの母線について覚えましょう。
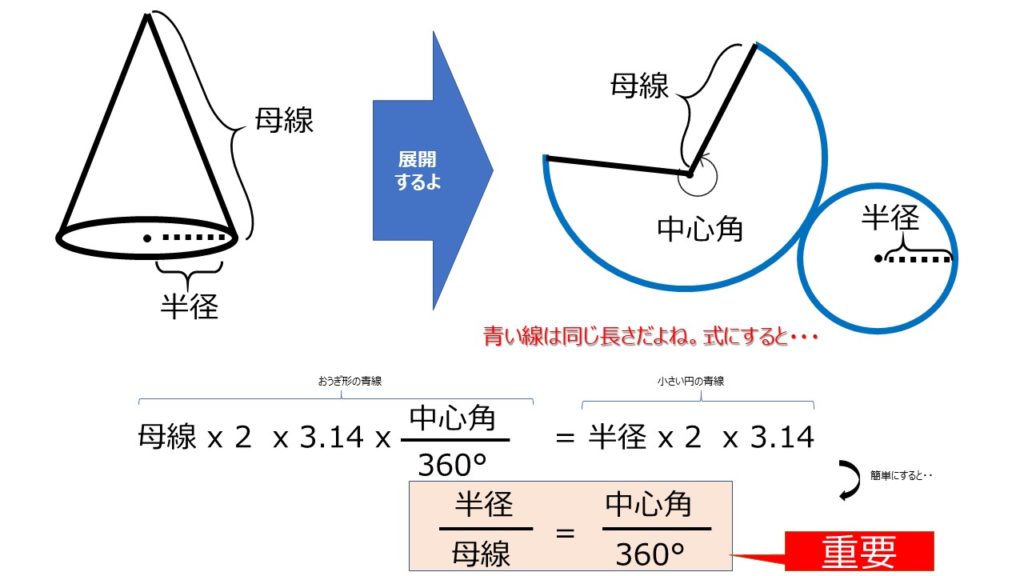
アプローチ③左2⃣
中心角は、母線の長さと底面積の円の半径、で決まります。(1)先ほどの式に当てはめて考えます。(2)比が分かれば、360°すれば中心角が分かりますね。
アプローチ③右1⃣
(1)母線分の半径、が6/10です。(2)計算に工夫するために、母線分の半径を使用します。(3)3.14の計算は最後にまとめます。補足では、下記の式の説明があります、覚えておきましょう!
円すいの側面積=母線×母線×3.14×半径/母線=母線×半径×3.14
アプローチ④左1⃣
37.68は12×3.14です。底面の半径は6cmとわかります。先ほどの問題であった、側面積の式から、求めることができます。
アプローチ④左1⃣
43.96は14×3.14です、底面の半径は7,とわかります。これから表面積を求めます。
アプローチ④右1⃣
円すいの上部分を切った下の体積です、円すい台です。もともとの大きな円すいから、上の小さい円すいが無くなったもの、として考えます。もともとの大きな円すいと上の円すいは相似の関係です。補足では真横から見て、三角形として考えるやり方の説明があります。
アプローチ④右2⃣
相似を使って考えます、底面積となる円の半径が分かるので、これらの比が高さの比ともなります。
前編2へ
アプローチ⑤1⃣
円すい台です、もとの円すいを復元して、取り除いた円すいを引きます。半径の比から、高さの比が4:5になっています、
アプローチ⑤2⃣
(1)円すいの展開図です。母線は12cmです、中心角は180°、から求まります。(2)母線の比が、12:16です。これから底面の円の半径の長さが分かります。補足では、母線と半径の比が同じ、から求めるようにしています。(3)円すい台の側面積も、全体の側面席から上の円すいの側面積を引きます。
アプローチ⑤3⃣
(1)円すい台の上の円の半径は、展開図の母線と中心角の関係から、3cmとわかります。(2)おおきい円すい、と小さい円すいの比が1:3から分かります。(3)表面積は、上下の円と、全体の側面積から、小さい円すいの側面積を引きます。3.14の計算をまとめてするようにします。(5)体積も全体から小さい円すいを引いて求めます。
アプローチ⑥右1⃣
長方形をぐるっと回します。ドーナツ型になります。(大きい円-小さい円)x高さ、になります。表面積はドーナツ型2つと、大きな円柱の側面積と、内側の小さな円柱の側面積、をたします。
アプローチ⑦左1⃣
体積は大きな円柱から、小さな円柱を引くイメージです。表面積は上下の円と、大きな円柱の側面と内側の小さな円柱の側面を足します。
アプローチ⑦右1⃣
回転軸の横に長方形がずれて配置されています。体積の場合は、そろえてあげて考えると簡単になります、大切なのは軸からの距離になります。でも、表面積はずらしてしまうと、元と同じではないので注意しましょう。
◆応用
アプローチ②右2⃣
真上から見ると輪郭が正方形、とわかります、正面から見ても、輪郭は正方形です。
アプローチ⑧1⃣
まずは体積だけ求めます。(1)円柱を求めます。(2)円すいになります。(3)円柱と円すいを合わせたものになります。
次に表面積を求めます。(1)上下の円と円柱の側面をたします。(2)円すいも底面の円と、側面(母線x半径x3.14)を合わせます。(3)円柱の側面と円すいの側面を合わせます。2で求めた値に、1の側面積をたすイメージです。
◆発展
アプローチ⑨1⃣
(1)下の直角三角形を上に持っていって、長方形を回転させたもの、として考えます。(2)中身がくりぬかれた円すい台になります。大きな円すいから、上の円すいとくりぬかれた円すいを引くようにしても求めます。まずは式を書いて、約分して計算していきましょう。(3)円すい台を求めます、大きな円すいから小さな円すいを2つ引くイメージなので、(2)と同じになります。補足では、(2)と(3)が同じになる説明があります。
アプローチ⑨2⃣
表面積を求めます。(1)円すい部分の側面積は同じになります。(2)大きな円すいから、上の小さな円すいを引く考え方ですが、くりぬかれた円すいの側面積は、大きな円すいから引く部分になるので、結局は大きな円すいの側面積を求めるだけで良いです。上下の円も、大きな円1つ、として考えましょう。(3)直角三角形を移動させて考えます、そうすると、(2)と同じ、とわかります。
まとめ
立体図形、回転させた体積/表面積は想像力が大事、と感じます、子供のころにブロックで遊ばせてたり、が大事なのかな。たくさん問題を解いて経験していくことで、得点アップを目指しましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント