算数の動画「数に関する問題」を見ました。
最大公約数、公倍数を駆使して、考えていきます。特にN進法、が新しい考え方です。でもテキストでは、N進法、に進む前に、解説がありますので、それを学んでから、順を追って進めていきましょう。

親としても順を追って教えてあげたいですね
N進法の説明
「N進法について アプローチ⑥に取り組む前に」、の説明があります。
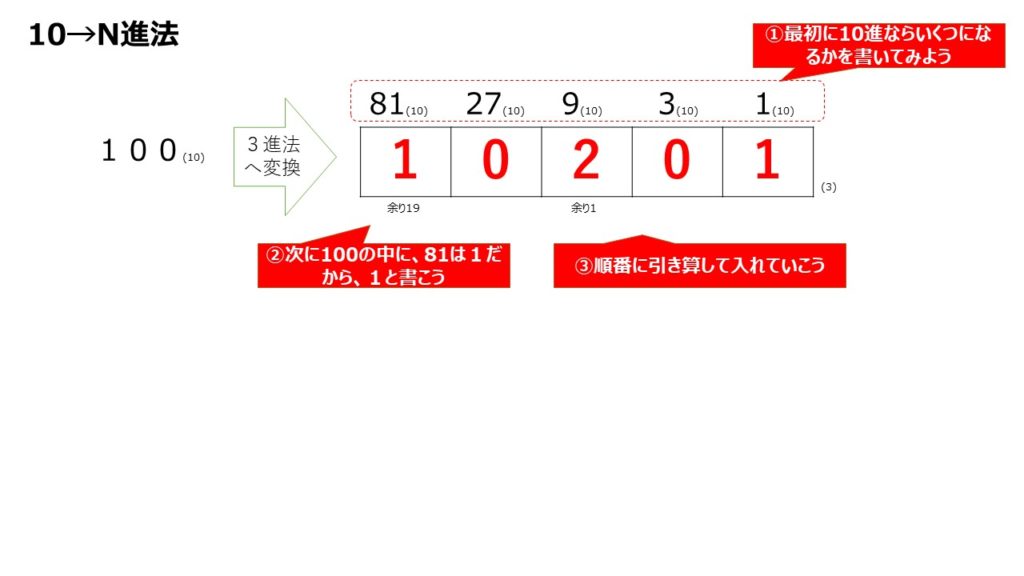
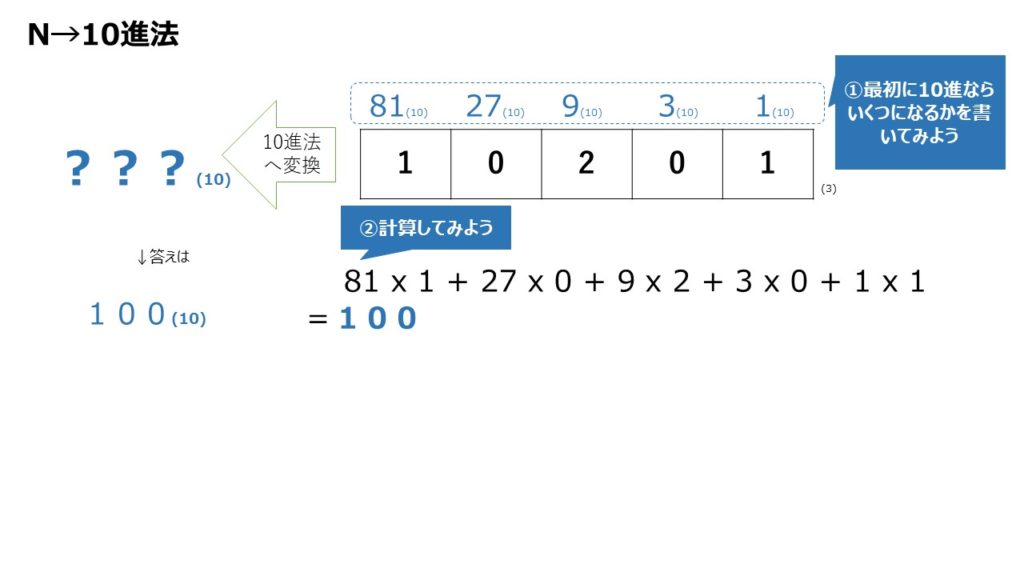
内容は、十進法と三進法を、とても分かりやすく説明してくれています!
この部分だけでも約6分ですので、自信なければ見ることをお勧めします。
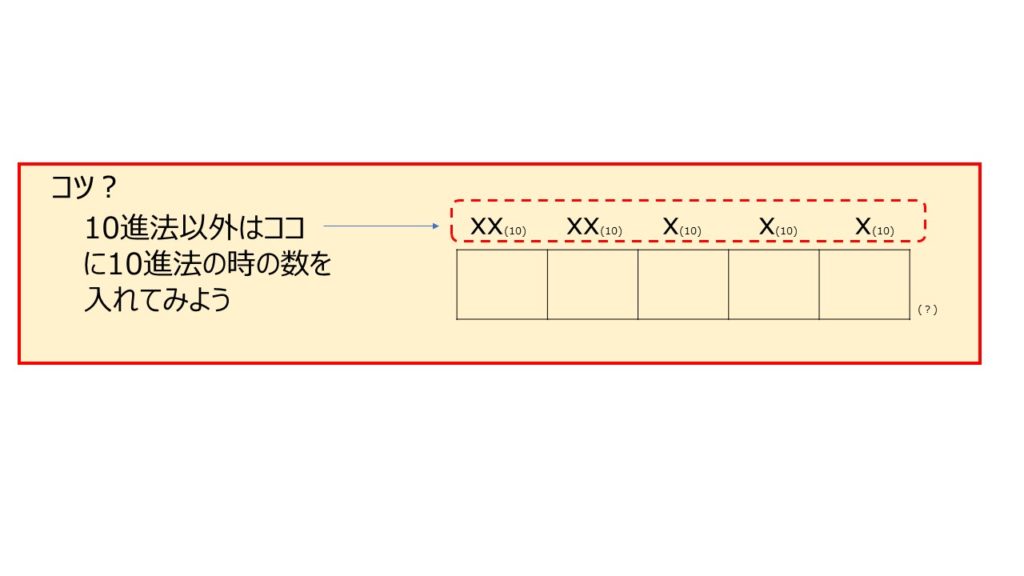
重要「N進法→N種類の数字」は覚えておきましょう。
・10進法からN進法への変換、N進法から10進法への変換
うちの息子君が良くわかっていないようだったので、、簡単にまとめてみました。
気を取り直して問題に進みましょう
◆基礎◆標準
アプローチ①左1⃣
最大公約数と最小公約数を求めます。A,Bとおくと、12で割ると、□と△とすると、□x△=15となるのは(1,15)と(3,5)です。AとBの和が96なので、□+△は8になるはずなので、(3,5)となります。
アプローチ①右1⃣
2つの整数を15で割ると、A,Bは□と△で、□x△=24です、(1,24),(2,12),(3,8),(4,6)ですが、(1,24),(3,8)に絞られ、そのうち和が小さい方になります。
アプローチ①右2⃣
A,Bとすると、6で割ると、□x△=108となります。(1,108),(2,54),(4,27),(6,18),(9,12)のうち互いに素、のものを探して、和が小さい方は(4,27)になります。
アプローチ②左1⃣
70÷□=△余り6、となりますので、□は64の約数、とかんがえます、残りも考えると64,48,32の最大公約数を考えます。最大公約数は16なので、1,2,4,8,16のどれかになりますが、あまりが6なので、6より大きい数が答えとなります。
アプローチ②右1⃣
7でわると4余る数は、4,11,18,25、、、、、となります。8で割ると2になるのは2,10,18、、、、となりますので、18が一番小さい数とわかります。次の数は、7と8の最小公倍数56を足した数です。つまり、18+56x□、です。これが600に近い数を探します。□が10,11で考えてみて、どちらが近いかを考えてみましょう。
アプローチ③1⃣
(1)すべての箱に、2個ずつ入れたのが最大です。27×2+9×2+3×2+1×2=、となります。(2)同じ様に、①27×0+9×0+3×2+1×1,②27×2+9×1+3×0+1×2、となります。(3)16点の時は(0,1,2,1)です。32点は(1,0,2,2)です。77点は(2,2,1,2)です。
アプローチ④1⃣
(1)Aは16個必要になります。(2)10この時は、(0,2,2)となります。(3)では、(2,1,2)なので、16×2+4×1+1×2、です。
アプローチ⑤1⃣
規則を確認します。塗られている場所で考えます。下段の右から1,3,9,27となっていることに注目します。(1)①は27×0+9×1+3×2+1,②は27×1+9×0+3×1+1×2、③は27×2+9×2+3×2+1×2=(27+9+3+1)x2=となります。(2)与えられた数字がどの桁の数より小さいか、から考えだします。
前編2へ
N進法について アプローチ⑥に取り組む前に
N進法をまずは学びます。10進法は今まで学んできた算数です。10個集まると次の位に行くものが10進法です。3進法は3個集まると次の位にいきます、1の位、3の位、9の位、27の位、となっていきます。とても重要なこととして、N進法はN種類の数字で表せています。
アプローチ⑥左1⃣
①4進法は、1の位、4の位、16の位なので、16×1+4×3+1×2、と10進法で表せます。②は8進数なので、64×6+8×2+1×3です。③3進法なので、(243+81+27+9+3+1)x2、で求まります。上級者向けの解き方として、3進法の1を足してあげると、729の位が1の3進法の数となります。これから1をひくと簡単に求まります。
アプローチ⑥左2⃣
①47を5進法に直します。1の位、5の位、25の位を使います、大きいくらいから埋めて進めます。②100を3進法に直します、81の位が一番大きいです。③63を2進法に直します、32の位が一番大きい数になります。
アプローチ⑥右1⃣
(1)カードは0~6までの7種類ですので、7進法、となります。x番目は10進法です。7進法の「0031」は7×3+1、で求まります。(2)7進法で「2516」は686×2+245×5+7+6、で求まります。(3)7進法で「6666」は(66+49+7+1)x6、で簡単に求まります。上級者向けの解き方では、前と同じ様に7進法の1を足して、全部が繰り上がって、2401の位が1の7進法の数になるので、そこから1引くと求まります。(4)10進法の「100」は、49の位から埋めて考えていきます。(5)10進法の「1857」は、343の位から埋めて考えていきます。補足では、割り算を使用して7進法に変える方法の紹介があります。
◆応用
アプローチ②左2⃣
あめは実際には149個、チョコは192個、グミは240個あれば足りる、と考えます。この3つの数の最大公約数48で考えます。この48の約数のうち、余り9個から、9より大きい数になります。グミが12個足りない、ことから、48と24はふさわしくない、とわかります。
アプローチ②右2⃣
7で割ると5あまる、13で割ると11余る、から、両方とも2足りない、とわかります。ので、7と13の最小公倍数91より2小さいもの、つまり、91x□-2となります。また、10で割ると6余るので、1の位が6とわかり、□には8が入ります。
アプローチ⑦左1⃣
点いている電球の問題です、動画の黒板ではすべてを分かりやすく書いて説明してくれています。(1)2進法の和で考えます。(2)2分28秒後は88秒後のことです。10進法で88を2進数に直します。
アプローチ⑦右1⃣
4種類の数字なので、4進法の問題となります。(1)10進法で30番目を、4進法で表します。(2)4進法で2103を10進法で表します。
◆発展
アプローチ⑧1⃣
ホテルの部屋番号です、8種類の数字で表します、8進法なのですが、使われている数字がずれています(4,9を使いません)。(1)8進法で「321」を10進法に直すと、64×3+8×2+1、となります。(2)ホテルの部屋番号567は、8進法では456、となります、これを10進法に直します。(3)10進法の「420」は8進法の「644」になりますが、これを対応している部屋番号に直すと「755」となります。
まとめ
ホテルの部屋番号の話は、問題としては難しいですね。雑談を息子君にしてみました。

日本では、死、を連想させる「4」とか、
苦、を連想される「9」は不吉だから、
ホテル番号にはあまり使われないんだよ。
海外だと、iPhoneも9をとばして、テンになったし、
Windowsも8の次は9をとばして10になったんだよ。
「4」とか「9」をとばす理由はいろいろあるみたいだけど、
逆に9が縁起がいい国もあるし、世界はいろいろだね。
息子君からは「ふーん」、で終わりました、、
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント