算数の動画「平面図形」を見ました。
基本的には、きちんと式を書く、後でまとめて計算する、という当たり前のやり方をきっちりすることが大切です。1つ1つは簡単かもですが、全体の処理能力を問われているかのよう、、、3.14の計算は最後にまとめてするようにしましょうね。しっかり図に書いて解き進めましょう。

円が転がる時にどこを通れないか、をしっかりと確認しましょう。
基本問題
・円が、長方形やおうぎ形の周りをまわって、その円が動いた面積を求めます。
・区切られた場所を通る場合、角の通らない部分を考慮する必要があります。下記のような部分ですね、これが何個ある、とかを図で書けるようになりましょう!
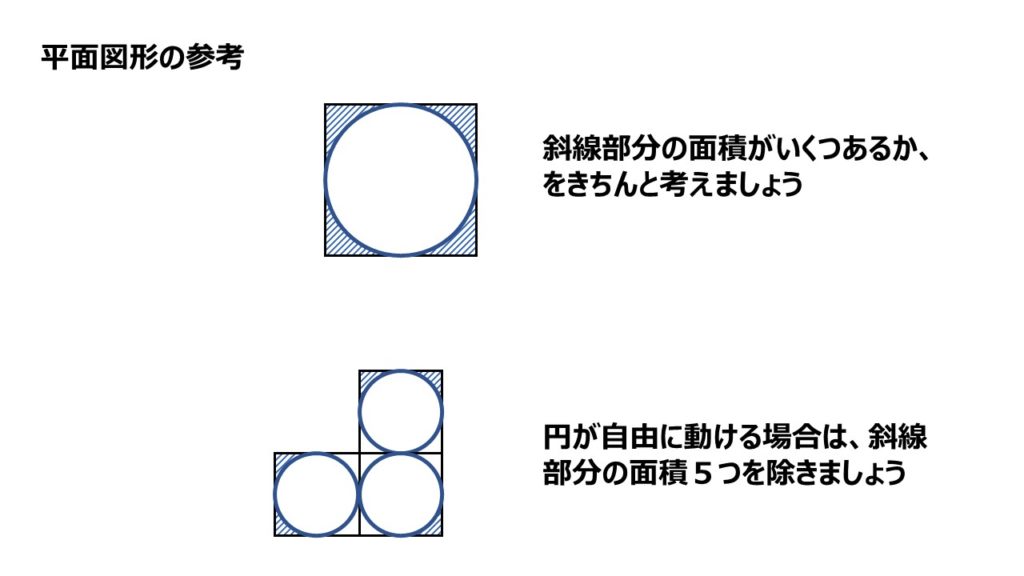
・四角形の内側を円が淵に沿って、中心が通った長さや、円が通過した面積を求めます。これも上と同じで、円が通れない角の部分を考える必要がありますね。
・半径の長さを比から、面積の比を用いて考えます。やっぱり、図を掛けることが大切ですね💦
◆基礎◆標準
アプローチ①左1⃣
円を転がします、角では円の直径が直角になるように回転させます。角はおうぎ形が4つ、残りは長方形4つ、を求めます。長方形はバラバラに求めても良いですが、真ん中の長方形の周りの長さの和に4を掛けて求まります。
アプローチ①左2⃣
平行四辺形の周りを円が動きます、「直径が直角」を意識します。図を書くと先ほどと同じ様に、おうぎ形4つと長方形4つです。おうぎ形4つは合わせると円になります。
アプローチ①右1⃣
今までと同じ様に考えます、おうぎ形4つを合わせると一つの円になります。長方形部分も、周りの長さに8を掛けて求まり、これらを足します。
アプローチ②左1⃣
おうぎ形の周りを円が転がります。円がおうぎ形の弧の部分をまわっています。角の部分は90度のおうぎ形が2つできます。おうぎ形の弧に沿って動く部分は、大きい半径10cmのおうぎ形から、小さい半径8cmのおうぎ形を引いて面積を求めます。
アプローチ②右1⃣
(1)半径3cmの円の中心が移動した部分が移動した距離は、円の半径の長さも足すのを忘れないようにしましょう。(2)半円2つと長方形、を足すと面積が求まります。
アプローチ②右2⃣
(1)円の中心が動いた距離です、中心は直角に動きます。中心の動いた距離を求めるので、半径を引くことを忘れないようにしましょう。(2)円が通過した面積です長方形部分は求まります。角の部分の一部が通れないことに気をつけましょう。おうぎ形や半円の部分が、円の4分の5倍で求まることに注意しましょう。動画では丁寧な解説があるので、お勧めです。
前編2へ
アプローチ③1⃣
正方形の中を円が辺に沿って転がります。(1)中心が通った長さは正方形の周りの長さから半径2つ引いた分の正方形になります。(2)円が通過した部分の面積を区切って考えます。隅の円を4等分して、一番端のおうぎ形1つと正方形3つ、として考えます。補足では、円が通過した部分の面積を正方形から引く方法の説明があります。通れない部分は真ん中の2×2と、4隅の部分です。
アプローチ④3⃣
正方形の中を円の中心が動く長さ、は半径を確認して解きましょう。面積は、全体から四隅と真ん中の長方形を引いて求めます。
アプローチ④4⃣
正方形の中を円が辺に沿って動きます、真ん中の通れない部分が無いので、円が通れない部分は4隅しかありません。全体から4隅を引いて求めます。
アプローチ⑥1⃣
(1)各おうぎ形の半径を求めます。(2)3つのおうぎ形は中心角が同じです、相似になります。3つの辺の比が1:2:3となります。(3)面積の比は、1×1:2×2:3×3=1:4:9となります。(4)3つのおうぎ形の弧の部分を求めますが、アの長さを求めて、後は比で6倍すると求まります。(5)アの面積を出して、これの14倍すれば求まります。
アプローチ⑥2⃣
(1)ア、イ、ウ、エの半径の長さを求めます。(2)全部相似なので(1)を比にします。(3)面積なので、1×1:2×2:3×3:4×4で求まります。(4)アの弧の長さを求めて、10(1+2+3+4)倍します。(5)アの面積を求めて、30(1+4+9+16)倍します。
アプローチ⑦1⃣
作図します。(1)Aを中心にして回転させ、次にFを中心にして、その次にEを中心にして、、そのその次にDを中心にして、と回転させるとCと重なります。(2)長さを求めるので、Cの弧の長さをもとめて、それに(1+2+3+4)倍します。(3)面積の比は1:4:9:16となります。アの面積の30倍となります。
◆応用
アプローチ②左2⃣
おうぎ形の周りを円が回ります。3隅のおうぎ形は90°と90°と120°の合わせて300°です。大きいおうぎ形は半径18cm、小さいおうぎ形は半径12cmです。あとは長方形を足します。補足では小さいおうぎ形の120°を出す時のいろいろな考え方の紹介があります。
アプローチ⑤1⃣
(1)円の中心が動く部分を線で書いてみます。一か所がおうぎ形の動きになります。それ以外の直線部分を丁寧に求めましょう。(2)円が通過した部分の面積を求めます。区切って求めます。通れない部分を間違えないようにします。動画では丁寧に説明がありますので、参考にしましょう。
アプローチ⑦2⃣
(1)巻きつける様子を書いて考えます、変わっていく半径の長さを間違えないようにします。(2)相似を使います、1:3:5が長さの比です。一番小さいおうぎ形の弧の長さを9倍します。(3)面積の比は1:9:25です、同じ様に、一番小さいおうぎ形の弧の面積を35倍します。
アプローチ⑧1⃣
牛を正六角形の柵につないでいて、牛の動きを図に書いて考えます。半径の長さに注意しましょう。図に書いて、各おうぎ形の面積を足します。中心角にも注意しましょう。計算は3.14を最後にまとめてするようにします。69×3.14をするだけにします。
アプローチ⑩1⃣
L型の6角形の中を円が動きます。方眼を作って考えると分かりやすいです、動画に分かりやすい説明がありますよ。方眼を利用して区切って考えます。四角形の数、おうぎ形の数、を数えます。動画の文字解説では、動けない部分の面積(4.3㎠)を出して全体から引く方法も紹介してくれています。
◆発展
アプローチ⑧2⃣
牛が正6角形の柵につながれている問題です、作図して考えます。3.14の計算は最後にまとめてします、80×3.14の計算になります。
アプローチ⑨左1⃣
ABを自由に動けるので、作図を間違えないようにしましょう。小さいおうぎ形2つ、大きい半円2つ、ABを1辺とした長方形、を足します。
アプローチ⑨右1⃣
CDの内側につながれています、どれくらい動けるかを作図する前に考えてみます。(1)外に飛び出るのは2mの90度のおうぎ形2つ分、と飛び出た長方形と、飛び出ていない長方形部分、に分かれます。動画で確認しておきましょう。(2)自由に動ける部分と動ける長さ、が変わります。柵の外側で動けるのは半径2mの半円2つ分です。柵内でも、一部動けない部分もありますので注意しましょう。
アプローチ⑩2⃣
6cmの方眼を書いて考えてみます。中心部分は動けますよ。半円2つと、6cmの正方形8個分、を足します。動画の説明はとても分かりやすいので、分からない人は参考にしましょう。
まとめ
丁寧に作図する練習をしておきましょう、特に柵の問題などはどれくらい半径が短くなって巻き付いていくのか、等を分かりやすく図に書けると良いですね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント