算数の動画「立体図形(2)」を見ました。
楽しんで考えて解く、もいいのですが、きちんと理由を考えないと解けないです、しっかり算数の問題です。想像力働かせつつ、頭の中で立体を想像して解いてみましょう。

空間把握の能力もあると良いですが、なくても訓練で何とかなりますよ
導入と基本①4⃣
立体をどちらから見ているか、をきちんと考えましょう。わかる高さを書き込んで解き進めます。黒板での動画で確認することをお勧めします。とても丁寧に図を書いて説明頂けています。
導入と基本②1⃣
確実にわかるところから、書きこんでいきます。
アプローチ①左1⃣
何処にあるかを見え方で考えます。個数が最大の時、個数が最小の時を考えます。重なって見える部分で最大にするか、最小にするか、で数が変わります。補足では、0個の見え方の補足があります。上から見て、右上に存在が見えているので、0個にはなりませんね。
アプローチ①右1⃣
隠れているところ、をきちんと考えます。最も多い場合、最も少ない場合を先ほどと同じ様に考えます。
アプローチ②1⃣
塗られている面を、数えます。(1)0面塗られているのは中心部分の2×2×2の8個です。(2)1面塗られているのは表面の真ん中2×2の4個です。これが6面ありますので、12個です。(3)2面塗られているのは、1辺のうちの真ん中2個です。これが全部で12辺あるので、12×2の24個です。(4)3面塗られているのは頂点部分の8個です。(5)塗られていない面の数を出します。「全体」から「塗られている分」を引く考え方です。立方体1個につき面の数は6、ので、全体4×4×4の64個あります。塗られている面+ぬられていない面の数は、(1個当たり6面)×64個の384面あります。塗られている面は表面積になるので、4×4×6の96面、とわかるので、塗られていない面は全体384から96面引いた数になります。別解では、切った部分の面積を考えて解きます。1回切ると2面出来るのが注意です。(切り取った面4×4)を2倍して、横に3回、縦に3回切れることから、4x4x2x3x3、で求まります。
アプローチ③1⃣
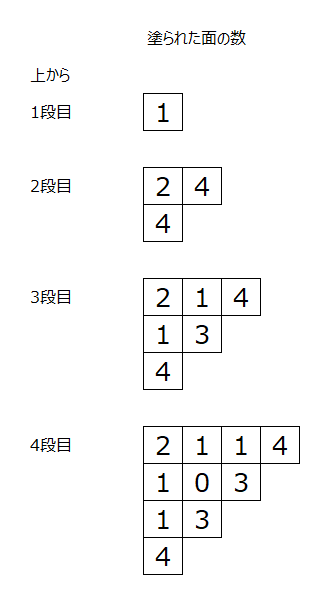
一段ずつ考えると分かりやすいです。(1)底を除くので、間違えないようにしましょう。上下左右から見ても同じなので、1x1x10×(底以外の見える方向5面)を掛けて求まります。(2)色が塗られている面について、今回は1段ごとに調べていきます。1段目は5面塗られています。2段目は2+4+4です。3段目は4+3+4+1+1+3です。4段目は、4+3+3+4+1+0+1+1+1+2となります。全部で20個あることを確認しましょう。
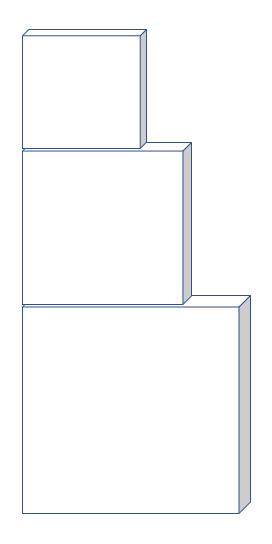
アプローチ④左1⃣
表面積を出来るだけ大きくします、このままの向きで積み重ねると間違えます。立体と立体の接している面が出来るだけ小さくする方が表面積は大きくなりますので、向きを変えます。全部立てて載せるイメージです。
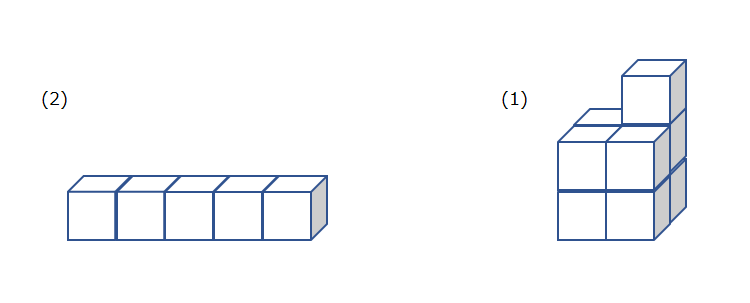
解法2は、接している面を引いていく考え方です。まず3つの直方体の表面積をそれぞれ計算します。それから、接する面を引きます。くっつけた時に表面積はそれぞれ2面分ずつ減ります。
アプローチ④右1⃣
辺の数を数えます。この(立方体14個でできている)立体について1つ確認しておきます。一番奥には1つ隠れていますよ。段ごとに分けます。上の段では4,下の段では12、が接しています。および上と下で接している5、を忘れないようにしましょう。
アプローチ④右2⃣
隠れている部分にも注意です、一番奥には1つありません。上の段と下の段で分けて考えます。上の段は5個、下の段は10個、上と下で接しているのが6個、併せて21個、となります。別解では、立体1つで6個面があるので、全体から表面積を引く、という考え方です。
アプローチ⑤左1⃣
(2)から解説があります。表面積を大きくするということは、出来るだけくっつける面を小さくするイメージです。横に並べてみます、まずは、こちらがシンプルです。そのあとに(1)の説明があります。表面積を小さくする→くっつける面を大きくします。
アプローチ⑤右1⃣
どの置き方が一番表面積が小さいか、、、分かりやすく説明頂けています。大きな直方体の3辺の長さはどのようなものが考えられるか、を考えます。動画は少し加工して丁寧に説明がありますので、動画確認をお勧めします。
・表面積が大きいのは、一番長細い直方体です
・表面積が小さいのは、凝縮しいて、立方体のような形です。
アプローチ⑥1⃣
立方体(切断する前の立体)について調べておきましょう、後でこの結果が使えます!最初に、面6、辺12、頂点8、と数を書いておいて、変化していくルールから考えていきます。頂点の数だけなので、8回切ります。元の立方体の面は形は変わるけど残ります、また、切った回数と同じだけ新たに(正三角形の)面ができますので、6+8=14です。
新たな立体の辺は、元の立方体のどのような位置にあるかを考えてみましょう。立方体の元の面1つに、4本ずつ辺があります。頂点は元の立方体の辺の数と同じだけあります。
(2)体積は切り取った部分の体積を求めて、全体から引きます。
アプローチ⑥3⃣
考え方は先程の問題と同じです、正二十面体の問題です。(1)面20,辺3×20÷2=30。頂点は3×20÷5=12、となります。(2)ここでも正二十面体(切断する前の立体)をリよすることがポイントになります。正六角形20個、正五角形12個なので、面は32となります。辺は30+5×12=90となります。頂点は5×12=60となります。
アプローチ⑦1⃣
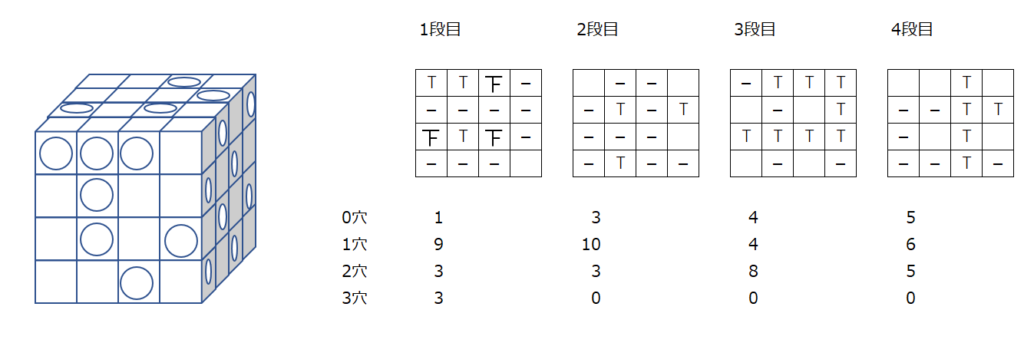
穴が開くところを、正、を書いて、カウントしていきます。正しくまとめられているか、確認してみましょう!
アプローチ⑧1⃣
一段ずつ考えます、クイズに近くなりますね。球が入っていない位置が分かりやすいので、まずは×を付けています。後は論理的に考えて解き進めます、動画での確認がとてもお勧めです。
今週の立体切断1⃣
外側に伸ばして考えますが、ひとつひとつ解くことで、最後の(5)の答えが導かれていきますので、順番にとき進めましょう。延長させると辺がクロスして砂時計型の相似の三角形が良くできますので、気付けるようにしましょう。
まとめ
立体三昧の単元でした。取組み方としてはクイズ的な遊びながらでも良いかもですが、途中で論理的に考える思考力も問われてるような気がします。なぜそうなるか、そう考えるのか、を納得しながら学んでいきましょう!動画はとても分かりやすく、理解の助けになりますので、お勧めしておきますね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント