算数の動画「拡大・縮小」を見ました。
長さの比を用いて面積の比などを求めていきます。相似ついては、ピラミッド型、砂時計型、を平行線から上手に見つけていきます。そこまで難しくないので、たくさん問題を解いて得意な単元にしておきたいですね。

拡大縮小などは、地図などで距離感を得るためには必要ですよ、地図の読める男女になりましょう!!
アプローチ①1⃣
砂時計型の相似の三角形です、初めは丁寧に解きます。(1)対応する角度を平行の錯角と対頂角で対応させます。(2)3:7の相似なので、合わせた10が28cmとわかることから求まります。(3)こちらはピラミッド型の三角形です。小さい三角形と大きい三角形は7:11の関係です。(4)4:9の相似から求めます。比のとらえ方についての別解では、1つの三角形の縦横4:3、から求めても良いです。
アプローチ②左1⃣
台形の中の三角形の面積比です、(1)台形をア、イ、ウ、エ、と4つに分けています。上底と下底の比が2:3なので、面積の比はアは2×2、イは2×3、ウは3×3、エは2×3、となります。覚えておきたいですね。(2)先ほどと同じ様に、上底:下底が1:4です、台形の考え方で、アは1×1、イは1×4、ウは4×4となります。そもそも全体が平行四辺形の為、対角線で面積は同じに分けられます、つまり、ア+エとイ+ウは同じですので、エは19、と求まります。
アプローチ②右1⃣
三角形の相似ですが、どこの長さが対応しているか、間違えないようにしましょう。(1)動画では丁寧に各角度を書き込んでどの角度が対応して相似になっているかを説明してくれています。直角と〇、直角と×、の各辺の長さが対応していることを分かりやすく説明があります。(2)また、解法1では、先ほどと同じ様に角度を直角・〇・×で分かりやすく説明があります。重なっている辺AHを連比して、求めることができます。解法2では、18cmと12cmで相似比が3:2、とわかります。これから面積比も9:4と分かります。これから、辺BHと辺CHが9:4とわかります。両方理解しておきたいですね。
アプローチ③左1⃣
3段のピラミッド型三角形の面積比の引き算です。真ん中の台形の面積比を全体の面積比の引き算などで求めます。5年生でも習いましたね。三角形は、小さい方から5:8:12なので、面積比は25:64:144です。2段目と3段目の台形の比は、引き算で、39:80と、分かります。
アプローチ③右1⃣
1本線を引きます。辺BFに平行な線をAからEFに向かって引きます。そうすると、左側ににピラミッド型の相似の三角形が3:4だとわかります。(1)辺EFが72cmは比4+56cm、なの、比3が12cmとわかり、xは比③+56cm、で求まります。(2)台形の面積の比を求めます。高さが分かりませんが、先ほどのピラミッド型の相似の三角形の比3:4から、高さを3:1とすることができます。
アプローチ④左1⃣
縮尺問題です。まずは分数で式を書いて、約分して計算します。(1)6cmを2万5千倍しますが、単位を合わせる為、100×1000で割ります。(2)10kmを2万5千で割りますが、単位をcmにする為、1000×100を掛けます。(3)7kmが14cmになるので、7kmをcmに合わせる為に1000×100して、これで14を割ります。(4)周囲70mです。比で考えますが比7が35mです。
アプローチ⑤左1⃣
縦横の長さの縮尺は、面積にすると、2回掛けないといけないです。はじめに単位の確認をします。下記を用いて問題を解きます。
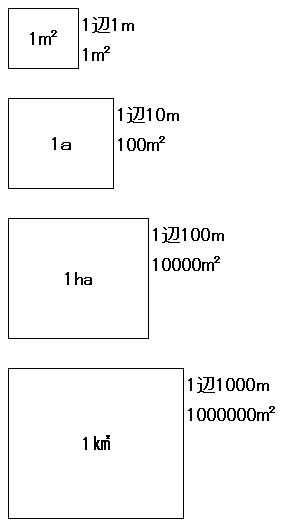
(1)面積の場合は、長さを2倍にすると、面積は4倍になります。面積を考える時は縮尺を2回かけます。約分を間違えないようにしましょう。(2)120aは、120x10x10、で、㎡になります、これに100×100を掛けて㎠になります。これを4000で2回割ります。(3)60㎠を実際の3375㎡で割りますが、単位をそろえます。これを計算すると、562500分の1、となりますが、これは面積の縮尺の為、長さの縮尺にするには、2回かけて562500になる数を探します。70と80の間にあることからアプローチします。
アプローチ⑤右1⃣
(1)(2)と順にヒントになっていきます、(3)は聞かれている長さを間違えないようにしましょう。
(1)EFの長さは、上底12cmと下底20cmの間、で求まります。(2)AEFDの面積は前の問題の答えを使って解きます。(3)全体の面積が分かるので、その半分が240㎠とわかります。(2)の答えから、三角形EFPが30㎠とわかります。これより、EPがわかり、答えのPBが求まります。別解は面積比を用います。三角形ADPと三角形BCPが同じなので、底辺の比の逆比が高さの比になります。
アプローチ⑥左1⃣
たくさんある平行を上手く利用して相似の三角形を探して解きます。一番大きい三角形と三角形HIP、一番大きい三角形とGFP、が相似になっていることからIP、FPがもとまり、これよりBDとCEも求まります。
ちなみに、この図では相似が7個あります、すべて分かりましたか?
アプローチ⑥右1⃣
砂時計型の相似ですね。何を求めたいか、から考えてみましょう。求めたいのは斜線の三角形の底辺です。一番小さい三角形はピラミッド型の相似の三角形になっています。三角形の縦と横のひが2:1になっているので、一番小さい三角形は5cmと2.5cmになっている、とわかります。これから横になった砂時計型の相似の左の三角形が22.5㎝、なので、求めたい斜線の三角形の底辺が求まります。
アプローチ⑦左1⃣
平行四辺形をメモリで分けています、平行四辺形の上の辺と下の辺を12と置いて考えます。真ん中の砂時計型の相似の三角形は2:3とわかります。三角形EFPは底辺4、高さ2、を÷2します。平行四辺形ABCDは底辺12、高さ5、となります。
つまり、三角形の面積は2で割ります、平行四辺形は2で割らないですよね。
面積比を書き込んでいった人もいると思いますが、長さ(底辺と高さ)を設定したほうが解きやすかったですね。
アプローチ⑦右1⃣
高さが同じなので、底辺の比から面積比も求まります。(1)平行線からピラミッド型の相似の三角形を探します。三角形ADCと三角形AGEの相似を使います、3:5になり、DGが3cmと求まります。(2)EFとFBの長さの比が求まれば答えが分かります。ピラミッド型の相似の三角形を探します、三角形BGEと三角形BDFです。(3)三角形CEFは2です。三角形CEBは5なので、全体の三角形は12.5とわかります。
アプローチ⑧左1⃣
どのピラミッド三角形を探すか、です。内部底辺の考え方、使いたいです。動画では丁寧な説明がありますので、是非確認しましょう。
(1)台形から要らない三角形を2つ引く方法で考えます。ピラミッド型の相似の三角形から長さを求めて考えます。(2)砂時計型の相似の三角形を使って、各三角形の長さを書き込んでいきます。斜めの三角形には内部底辺の考え方で解くことができます。是非とも覚ええおきましょう。
アプローチ⑧右1⃣
直線DBは点Qを通るのか、をまずは確認しましょう。動画での説明が分かりやすいですね。台形の対角線を引くと両端の三角形の面積が同じになります。および、両端の三角形の内部底辺の長さが同じ、とわかります。つまりこの考え方から、直線DBは点Qを通る、と分かります。
台形の対角線が線PRで二等分されています。砂時計型の相似の三角形が1:2とわかりますので、PRは20cmと20cmで分けられた、とわかります。これから面積比を求めることができます。
別解は平行となる補助線を引いて考えることで解くことができます。これも動画がとても分かりやすいです。
実戦編C4⃣
たくさん相似となる三角形あります、全部でいくつか、数えてみましょう。(1)30度、60度、90度の三角形を探します、90度に注目して探してみましょう。動画では分かりやすく色を付けて説明があります。(2)30度、60度、90度の三角形は正三角形を2つに分けた時の三角形です。60度を挟んで辺の長さが2:1になっていることを覚えておきましょう。(3)ピラミッド型の相似の三角形1:4が隠れていますので、探して解きます。別解では、60度を挟んで辺の長さが2:1を使った解き方の説明があります、確認しておきましょう。
今週の立体切断1⃣
図1
平行な面にある直線は平行になります。下記は覚えておきましょう。図1は長方形になります。
平行四辺形は、2本の対角線の長さが異なります。
長方形は、2本の対角線の長さが同じです。
図2
見た目で平行四辺形、と答えてはいないですか?切断面の4辺の長さが同じですので、正方形かひし形、のどちらかです。切断面の対角線の長さが異なるので、ひし形、となります。
ひし形は、2本の対角線の長さが異なります。
正方形は、2本の対角線の長さが同じです。
図3
左の面を確認すると、1:4の三角形、右の面の三角形は3:4、なので、平行ではないことが分かります。同じ様に手前と奥の面も比が異なっているので、これは切断面としてあり得ない、と判断できます。
図4
ひとつひとつ、切断される点を考えていきます。これは切り分けていない(途中で切ることをやめた図)ので、あり得ない図、となります。
図5
右面と左面は2:1になっているので、平行です。奥の面と手前の面は奥が3:4なので、手前も3:4になっている必要があります。五角形になっています。
まとめ
内部底辺は以前も出てきましたが、なかなか使いこなすのは、レベルが高いですね💦縮尺を用いて拡大縮小する計算は単位に気を付けて、まずは分数の式を書いて約分して計算をラクにしてしまうことが大事です。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント