算数の動画「点の移動」を見ました。
点がグルグル移動していきます、2つの点だったり、シャドーという考え方を用いたりします。基本として、図に書いてみる、というところから始めるとよさそうです。約2時間の長編ですが、一つ一つの説明がとても丁寧ですので、分からない人は動画をみて確認しておきましょう。

イメージできない時は、図に書いてみましょうね
アプローチ①左1⃣
基本問題です、グラフを見てどういう図になっていくかを考えましょう。まずは図で確認することが大切です。グラフの中でも三角形の相似がつかえます、360:144=5:2から、30×(2/5)でも求まります。いろいろな解き方があるので、動画で確認しておきましょう。
アプローチ①右1⃣
どういう形になっていくか、面積の比を底辺で比べたり、と、基本が詰まっています。問題文にある条件は図に書き込むようにしましょう。(2)求める三角形を間違えないようにしましょう。5秒後なので、高さが同じで底辺が違う三角形の面積比を考えます。(3)面積が半分、ということは、高さが同じで底辺の長さが半分になるタイミングを考えます。
アプローチ②左1⃣
台形で考えます。Pの動きをまずは確認してから問題を解きましょう。(1)秒速は24÷12、で求まります。(2)(1)の答えから、台形の各長さを書いておきましょう(3)三角形ABCの時、で考えます。(4)底辺が同じで高さが違う三角形、で考えると良いですね。グラフを利用するのもありです。両方できるようにしておきたいですね。
アプローチ②右1⃣
点Pと点Qが動います。速さの問題や等差数列などを使います。(1)120cm動きます、速さの和で割ります。(2)240cmを速さの和で割ることになりますが、これは1回目に出会ってから2回目まで、の値です。
アプローチ②右2⃣
点Pと点Qが同じ方向に移動します。池の周りをグルグル回る問題に似ていますね。(1)初めの差が120cmなので、これを速さの差で割ります。(2)1回目から2回目までに出会うまでの時間は240÷3、の80秒後、となりますが、これは1回目に出会ってから2回目まで、の値です。
アプローチ③左1⃣
点Pと点Qが同じ方向に移動します。解説も確認しておきましょう。(1)距離が70cmになる値を探しますので、速さの差で割ります。(2)同じ辺上になる時間を考えます。(1)を利用して、1辺と同じ距離の差、から、後何秒後で同じ辺上になるか、と考えます。少し難しいかもですが、動画で確認してみることをお勧めします。
アプローチ③右1⃣
まずは問題の内容を確認します。甲が先に進んで、甲が曲がってしまうと、乙から見えなくなります。また、乙が追い付いても甲と同じ辺にいれば見えます。甲と乙が各頂点に来る時間を書きこんで考えます。甲が見えない時間は、5秒から6秒までの1秒間、225秒から30秒までの5秒間と、30秒から36秒までの6秒間と、50秒から60秒までの10秒間を足したものになります。補足では、乙から甲が見えている時間を考えて、60秒から引いても解けます。別のまとめ方として線分図でまとめています。線分図でまとめても分かりやすいですね。
アプローチ④A1⃣
どれだけ進んだか、を図示して考えます。(1)初めて半分になるのは、AP+BPが全体240÷2の120となる時、で考えます。これは120÷(6+4)=12秒後、とわかります。(2)初めて長方形になるのは下記の時です。これはPとQが合わせて240進んだ時です。
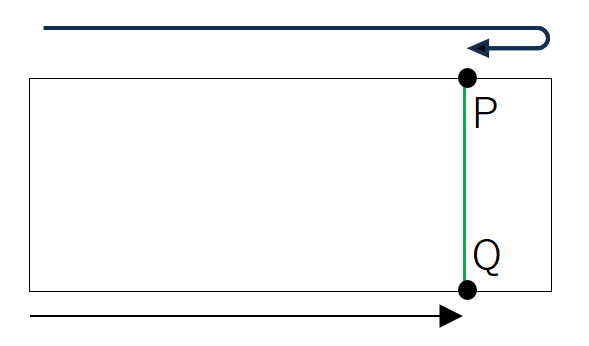
(3)2回目に半分になる時は、(1)を上手く用いて考えます。これは120×3の360がPとQが進んだ合計なので、360÷(6+4)で求まります。
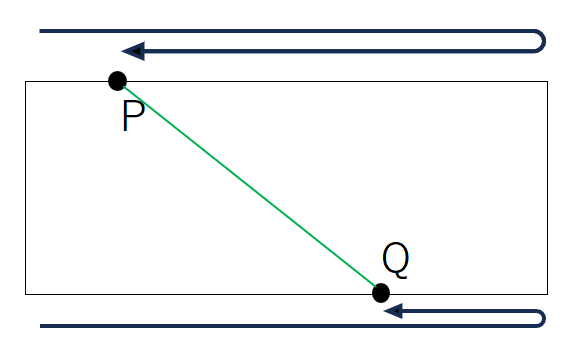
補足では、長方形の面積が半分になる時は、長方形の真ん中を通ります。
アプローチ④A2⃣
先程同じ様に、図に書き込んでPとQの動きをイメージしながら解きます。図に書いていくことが大切です。(1)1回目に半分になるのは、PとQが合わせて120進んだ時、になります。(2)2回目に半分になるのは、先ほどの問題と少し違います。Pがとても速いので、下記状況となります。今回は差が分かります、P-Qが120です。差が分かったので、120÷(7-3)で求まります。
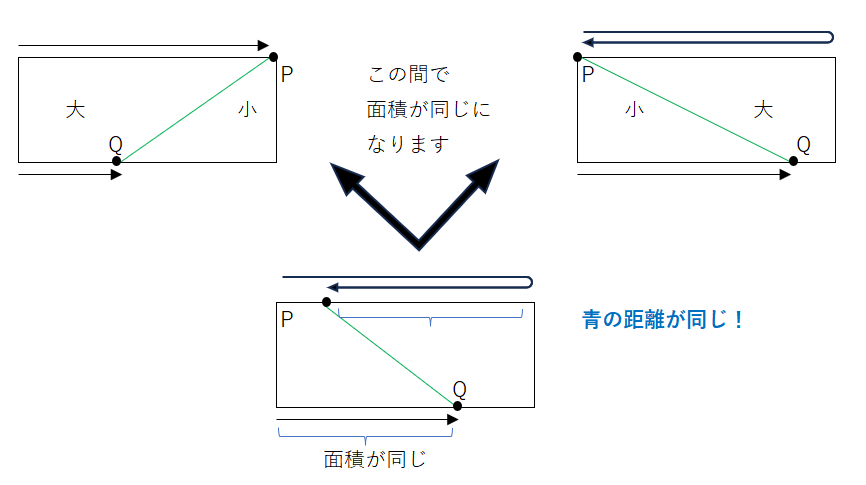
アプローチ⑤左1⃣
シャドー、という考え方です、解き方です。使いこなしましょう。(1)ピラミッド型の相似で解きます。比5+比2が126cmとわかります。シャドーの考え方の説明もあります。Qが動いた時にQCと真ん中の線で交わる点をQ´(これがシャドー)として考えます。Q´はQの速さの半分なので、それを利用して解きます。
アプローチ⑤左2⃣
Pのシャドーを使いこなして解きます。Qのシャドーもありますが、Pの方が分かりやすいですね。P´のシャドーを書き込みましょう。P´は速さは12ですので、112÷(12+2)で8となります。別解ではQのシャドーを考える説明があります。Q´は前の問題のように使えませんので、使う場合は、QCと真ん中の線が交わる中心の点がスタートになります。
アプローチ⑤右1⃣
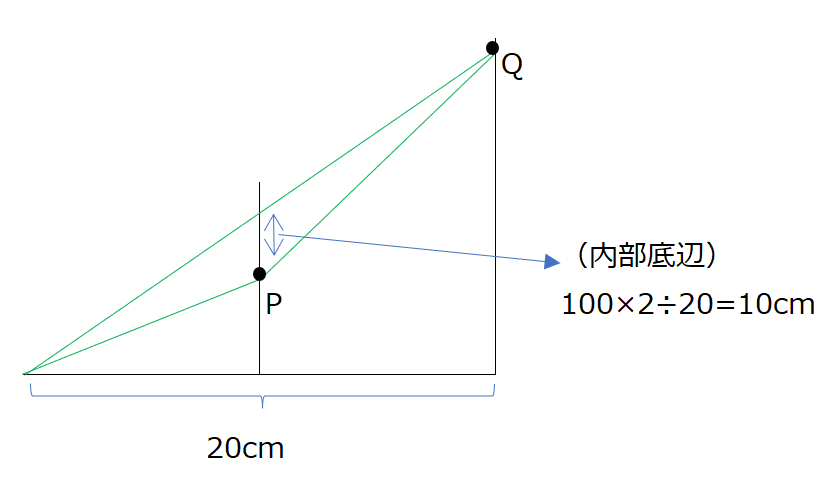
上下の動きの問題です。内部底辺で考えます。(1)PとQが進んだ距離は170cmなので、速さの和で割ります。(2)APQが一直線になる時です、これはQのシャドーを使います、Q´がPと同じ辺上を進みます。Q´の速さは7cm/秒です。P+Q´=170となる時が直線になるので、170÷(3+7)で求まります。(3)内部底辺が10cm、となる時を考えます。Q´のシャドーを用います。1回目はP+Q´が160となる時です。
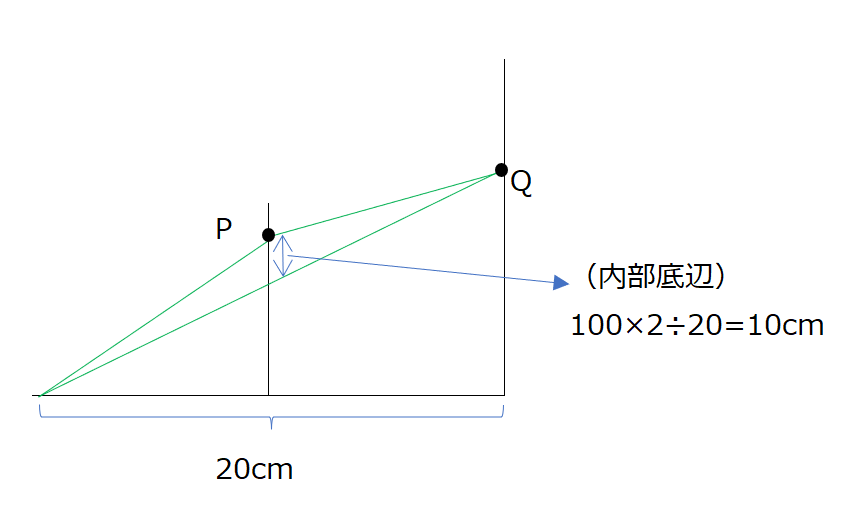
2回目はP+Q´が180となる時です。
アプローチ⑥A1⃣
甲乙の動きを図に書いて考えましょう。動画では各状況を図に書いて分かりやすい説明があります。(2)シャドーを使って解きます。別解では上級者向けの説明があります。解き方は理解しておきたいですね。
アプローチ⑥B1⃣
P、Q、Rと3つ動きます、一つ一つ考えていきましょう。(1)各点の速さを間違えずに求めましょう。(2)ピラミッド型の相似を使って長さを考えます。(3)なかなか難しいので、動画での確認をお勧めします、、、先生の説明は分かりやすいですよ。
アプローチ⑦1⃣
問題を読んで動きを理解しましょう。2点の動きは、Cまで行っており返して戻る動きです。(1)Pが78sm多く進んだ時間をPQの速さに差から求めます。(2)P+Qの和が、縦×2,横×3、の和です。速さは和になります。(3)Pが138cm分多く進んだ時なので、速さの差、で割ります。(4)P+Qが126cmなので、これを速さの和で割ります。面積の比は台形の場合は上底と下底の長さの比ですね。
今週の立体切断1⃣
砂時計型の相似の三角形の比を上手く使いこなします。
今週の立体切断2⃣
(5)の解説と補足が動画では説明があります。体積は先っぽの三角錐を引いて考えます。手前と奥の立体は半分半分となっています、動画では、奥の立体と手前の立体を色を分けてならべて説明がありますので、確認しておきましょう。
まとめ
動画でも何度も先生が伝えてくれていますが、個別に動きをきちんと図に書いたほうが良いですね。イメージできればいいですが、イメージできるまではたくさん図を書いて考えていきましょう。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント