算数の動画「和と差に関する問題」を見ました。
ベン図から線分図、平均算やつるかめ算的なものが3種類になったり、表に表してみたり、と、手を変え品を変えいろいろ出てきます、問題の趣旨をつかめれば解けると思うのですが、それが難しいでしょうか・・・

全部の動画は長いので見れなくても、分からない問題は動画で見ておくことをお勧めします!
導入と基本③4⃣
解法1ではベン図で解きます。クラス全体を①とします、水泳が好きなのは⅔、登山が好きなのは¼、両方すきなのが⅙、で、どっちも嫌いな人が18人です。ベン図を使うので、まる二つ部分がいくつか、と考えると⅔+¼-⅙より、¼、とわかり、これが18人になります。これらから全体は72人となり、両方好きな⅙は12人、とわかります。
解法2では、表で考えます。黒字部分は問題文の通りです。下記の赤太字を書き込んでいくと、18人が¼、とわかります。
| 登山 〇 | 登山 × | 計 | |
| 水泳〇 | ⅙ | ½ | ⅔ |
| 水泳× | ⅟12 | 18人 | ⅓ |
| 計 | ¼ | ¾ | 1 |
両方使えるようにしましょうね。
アプローチ①左1⃣
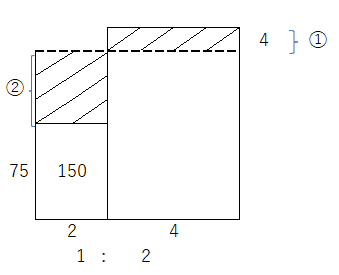
平均算です、面積図で解きます、5年生で習いましたね。ABよりもCDEFの方が点数が高いですね。②が8点、とわかるので、全体は75+8の83点、とわかります。
アプローチ①右1⃣
買う量が増えると値段が変わりますね、平均算ですね。3つを2つにして解きます。
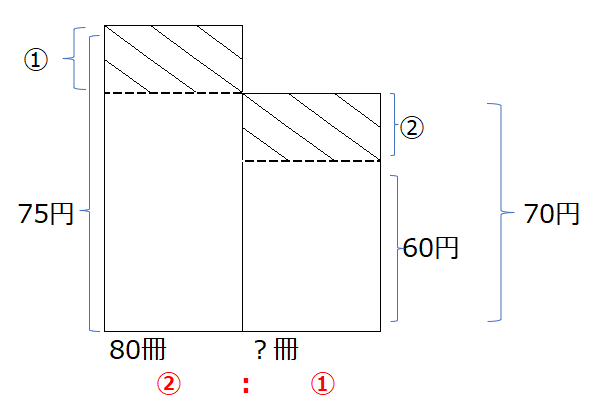
(1)1~20冊の合計が1800円です、21~50冊は1冊80円なので合計は80×30=2400円、51~80冊は1冊60円なので、合計は60×30=1800円、なのですべて足すと6000円となります、これが80冊の合計なので、平均は、6000÷80の75円、となります。
(2)(1)の結果を使うと、下記面積図が書けます、今回は縦軸の金額から、斜線部の面積の縦の比が分かるので、赤字の横の比も求まり、?冊は40冊、とわかります。
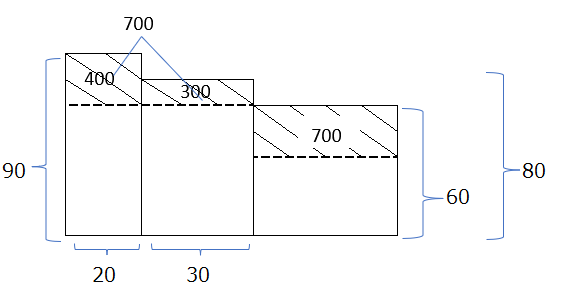
別解では3つのままで図に書いて解きます。わかる部分を埋めて解き進めてみましょう。
また、アプローチ①右2⃣(2)の問題は、今とは少し問いがかわっています。時間に余裕がある人は、ぜひ解いてみてください。
アプローチ②左1⃣
消去算です。問題文を下記の様に式にします。
大×3=中×4+小×5
大×3+中×2+小×1=4200
中×2+小×3=1600 ←①
太字の大×3は中×4+小×5、に置き換えることができます。
中×6+小×6=4200 です、これを簡単にすると
中×1+小×1=700 となります。
黄色の式を見比べて、中を消すために中×2にすると、
中×2+小×2=1400 ←②
①と②から小×1が200円、中×1が500円、大×1が1000円、とわかります。
アプローチ②右1⃣
上茶、下茶の問題です、問題文を読みましょう、kg当たりの値段ですので、併せて何kgになって、合計何円になるか、を考えます。上茶1kgを①、下茶1kgを1⃣とすると、①+3⃣=630×4=2520円、②+5⃣=640×7=4480円、です、この2つの式から、それぞれの⓵と1⃣を出します。
アプローチ③右1⃣
表にまとめると、分かりやすいです。きちんと書きましょう。
| 得点 | 100 | 75 | ア | 60 | 40 | 35 | 25 | 0 |
|---|---|---|---|---|---|---|---|---|
| 人数 | 4 | 12 | イ | 9 | ウ | エ | 3 | 0 |
| 1番(25) | 〇 | × | 〇 | 〇 | × | × | 〇 | × |
| 2番(35) | 〇 | 〇 | × | 〇 | × | 〇 | × | × |
| 4番(45) | 〇 | 〇 | 〇 | × | 〇 | × | × | × |
1番が出来た人は4+イ+9+3=27人です、2番が出来た人は4+12+9+エ=29人、3番が出来た人は、4+12+イ(11人)+ウ=34人、です。
アプローチ③左1⃣
同じ様に表を作成して解きます。5点が2つに分かれます、問題文の残りの条件と作成した表を合わせて考えて解きましょう。
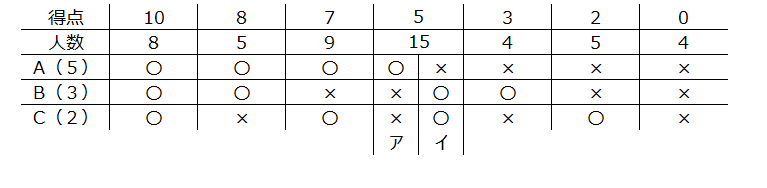
アプローチ④右1⃣
ベン図でもとけますが、線分図でも解けるようにします。(1)動画ではベン図での説明があります。両方できた人は18人が最大です。最小はゼロ、はできません(合計で40人を超えてしまう)ので、少なくとも8人以上は両方できた人が必要です。別のまとめ方として、線分図で考えることができます。
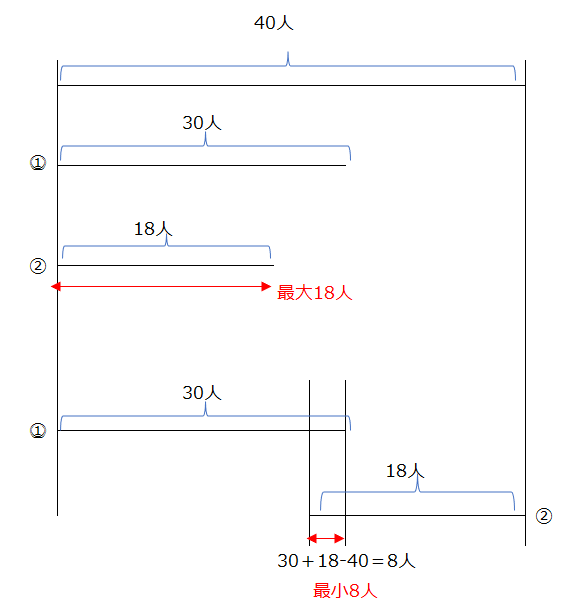
(2)も線分図で考えています。動画での説明が丁寧で分かりやすいです。
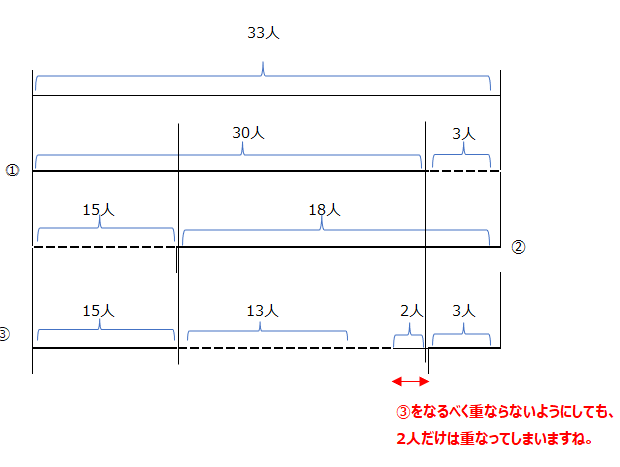
追加問題があります。応用問題なので、算数が得意な人向け、になります。これは④右1⃣の改題です。問題:子供33人いて、1番〇が30人、2番〇が18人、3番〇が20人です。3題ともできた子供は、□人から□人までです。
解説:最大は18人、となります。最小は③を重ならないように配置しても、2人は重なってしまいますね。
アプローチ⑤左1⃣
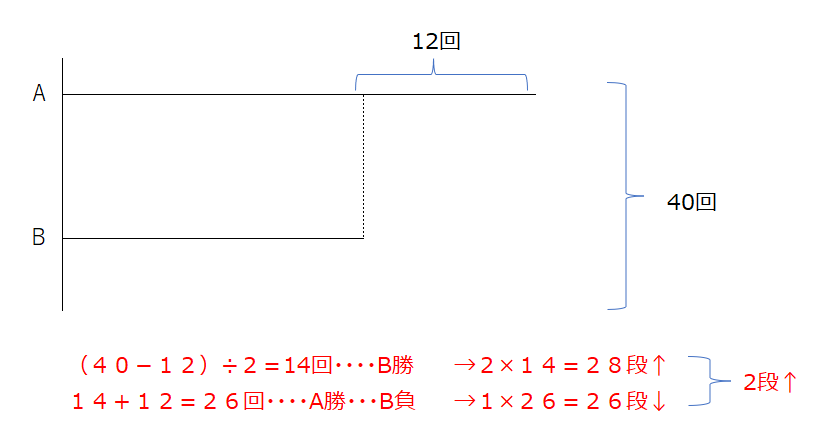
和差算でも解けます。勝ったら2段↑、負けたら1段↓、です。1回じゃんけんすると差が3段になりますので、差が、36段、ということは、Aが12回勝てばよいです。全部で40回したので、残りの28回は差がつかなかった、となります。
アプローチ⑤右1⃣
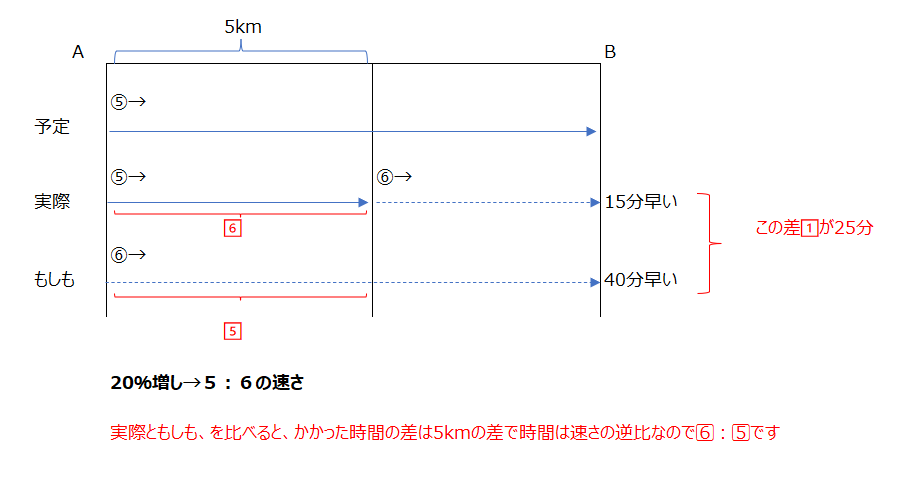
図式化すると、分かりやすいです、動画も分かりやすいです。6⃣は150分なので、5÷150÷60、で求まります。
アプローチ⑥左1⃣
分かる部分から順番に解いていきます、面積で求めていきましょう。3つのつるかめ算でも解けますが、AとBはまとめて解くこともできます。(1)は下記から面積図にてつるかめ算を実施します。
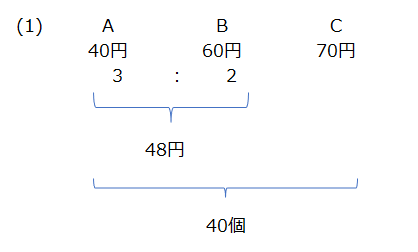
(2)一番下の段を切り離すイメージで解きます。
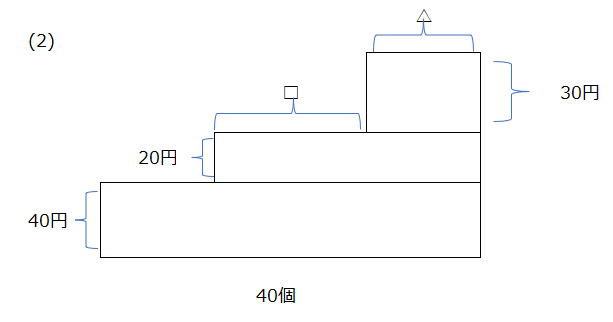
アプローチ⑥右1⃣
BとCの平均を出せば、2種類になるので、解きやすくなります、まとめてから面積図で解きます。

別解では、表で解きます。極端な値から、ずらして考えます。一つ右にずれると、Aはー200円、Bは+80円、Cは+70円なので、合計は-50円です、-500円になるには右に10回ずらすことになるので、Cは10、とわかりますね。
3つまとめて解いいますが、どちらも分かりやすいですね。両方理解しておきましょう。
| A(100円) | 37 | 35 | ・・・・ | |
| B(80円) | 3 | 4 | ・・・・ | |
| C(70円) | 0 | 1 | ・・・・ | |
| 計 | 3940 | 3890 | 3440 |
アプローチ⑦右1⃣
まずは、導入問題でこの考え方を理解して上で、本問にすすみます。解説は分かりやすく、考え方を説明してくれています。この考え方を用いて、考え直してみましょう。
導入問題:
A,Bの2種類の棒で教室の幅を測ります。教室の幅はAの棒はちょうど3本分、Bの棒はちょうど5本分です。Aの棒1本と、Bの棒1本の差が48cmである時、教室の幅は□mです。
解答:
答は3.6mです、単位変換は間違えないようにしましょう。
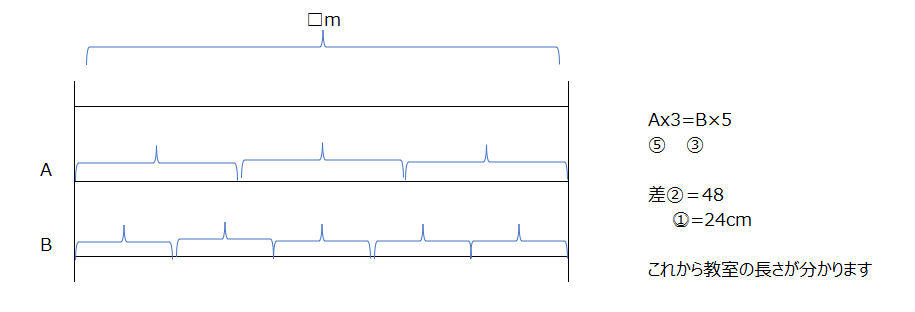
上の導入問題を分かれば、この問題は難易度が下がります、同じ要領で解きましょう、
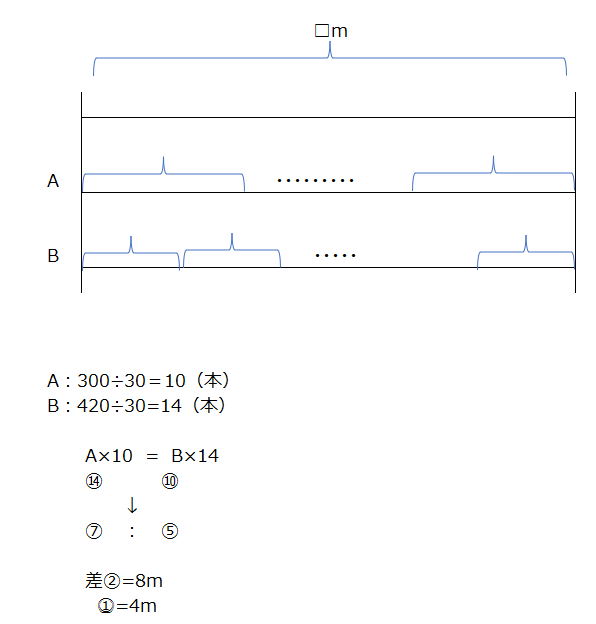
アプローチ⑦左1⃣
先程の問題と同じように考えていきましょう。小数になりますが、同じ様に考えていきます(1)A:4920÷100=49.2本、B:5040÷100=50.4です。A:B=50.4:49.2=42:41となります。この差が2.4mになります、これからAとBの長さが分かりますが、Aは100.8m、Bは98.4mなので、100mとの差がくるいになります。(2)(1)の値から解きます。
アプローチ⑧右1⃣
5つの整数を、A<B<C<D<Eとして解きます。すべてのケースを書き出すと解きやすくなります。

実戦編A1⃣
問題の意味をきちんと理解しましょう。7個の数を1個と6個に分けます。7個の和が70です。
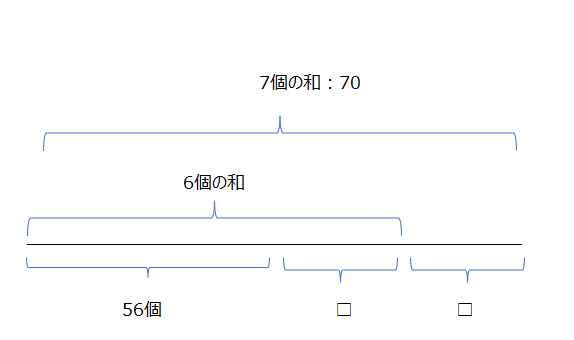
実戦編A4⃣
図で書く癖をつけましょう、合計得点で考えます。

実戦編B2⃣
うまく消去算を使いましょう。
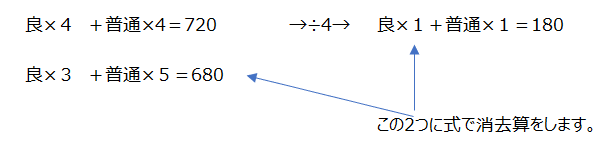
和差算では、差が40円、とわかり、これから解くこともできます。
今週の立体切断1⃣
切断面は間違いなく出せましたか。三角すいの引き算ですが、最後に問われているのは、大きい方の体積です。
まとめ
いままで習ってきた個別単元(消去算、和差算、平均算、つるかめ算、ベン図、、、)などが一挙にまじりあって出てくる感じです。とはいえ、問題の問われていることをきちんと読み取れれば、どう解いていくかを分かりそうです。解き方を覚えておくだけでなく、考える力が大切ですね、理解できるようにしましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント