算数の動画「場合の数(1)」を見ました。
確率を「確からしさ」という言葉で習います。確率と聞くとなじみがありますかね、何事でも確率高い方が良い、って考えますよね、今後の人生でも使うことが多いので、しっかり学んでほしいです。

ギャンブルとかも確率論がたいせつですよ♪
導入と基本②4
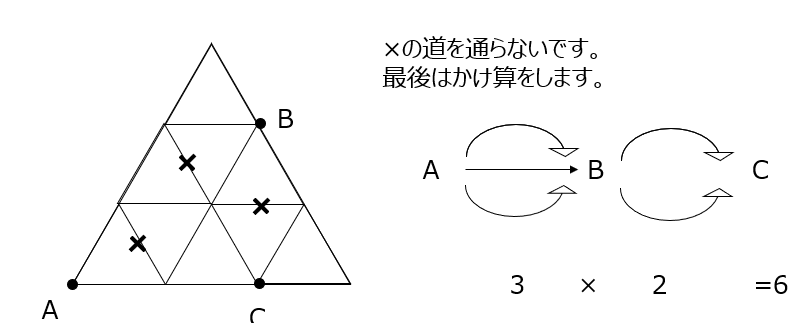
三角形の道順の問題です。遠回りをしないように考えます。最後は掛け算になりますよ、足し算にならないですよ!ここ間違えた人は、動画参照です!
導入と基本③2
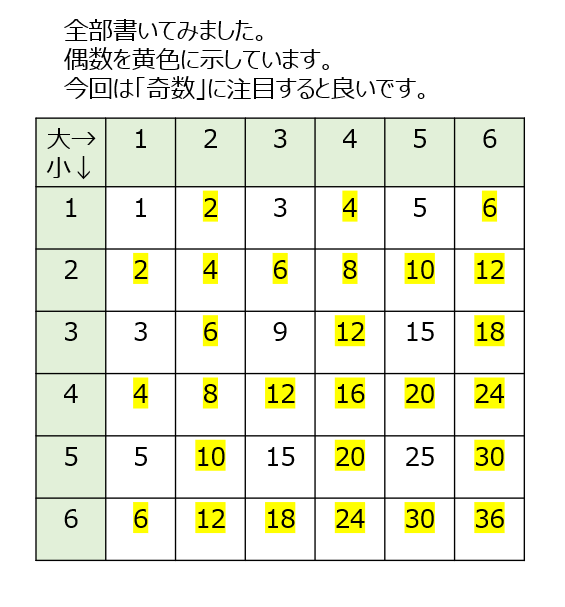
サイコロの偶数になる確からしさです。動画では全部書き出してくれています。動画では奇数が少ないのでそちらを求めて、全体から引き算しています。少ない方に注目するのが大切な単元ですので、心してかかりましょう。「確からしさ」とは「確率」のことですね。計算式で解ける様にしましょう!

導入と基本③3
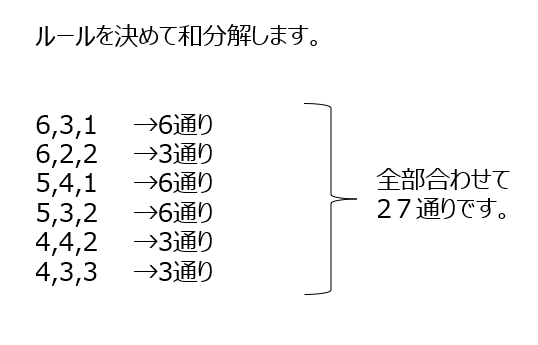
サイコロの問題です。ルールを作って、漏れなく書き出せる様にしましょう!順番があるので、各ケースで何通りかを求めて足します。
導入と基本③4
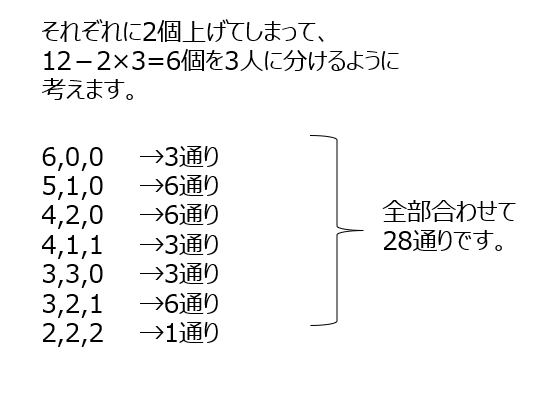
先程の問題と同様に漏れなく書き出します。3人とも同じ個数の場合は、1通りです。
アプローチ①1245
1 白と青が決まれば赤は自動的に決まります。
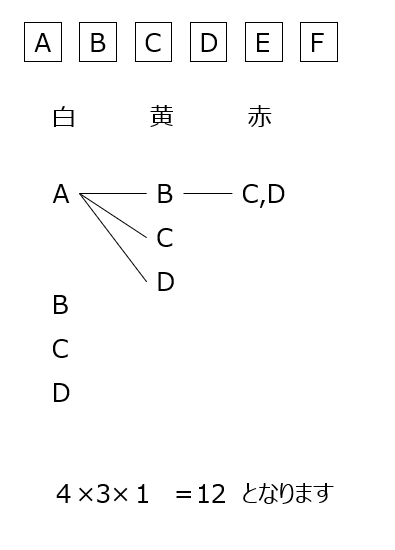
2 赤2つを決めれば、白2つも自動的に決まります。

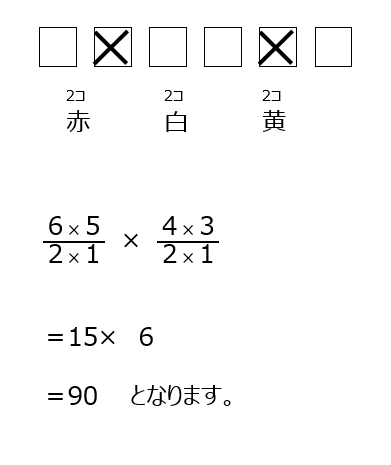
4 数の少ない黄色から決めて、白が決めて仕まえば、赤は自動的に決まります。白は区別無いので2で割らないといけないですよ。

5 赤、白から入れたとして、区別無いので2で割って決めていきます。※この考え方は基本ですね、完璧にしておきたいです!
アプローチ②1
(1)区別ないので割ることを忘れないようにします。8人から5人選ぶのは、8人から3人選ぶのと同じです。

(2)黒だけを考えれば解けます。

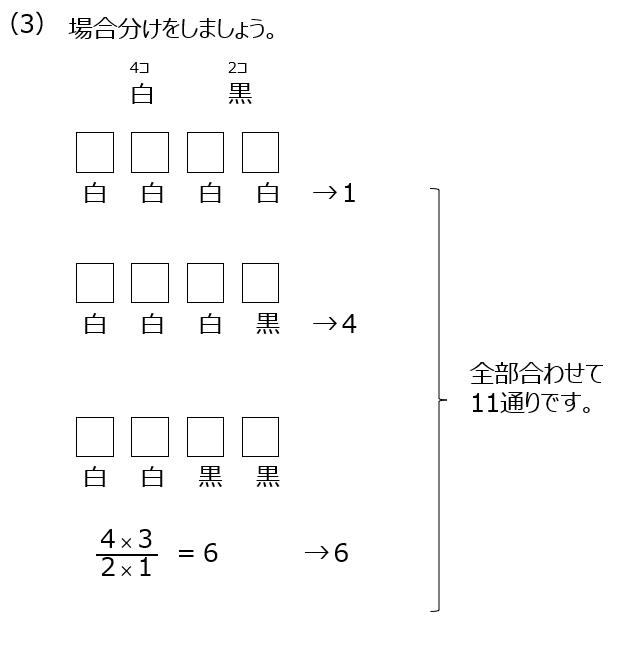
(3)場合分けをキチンと考えて進めます。全部白、1つだけ黒、白2つ黒2つで考えます。
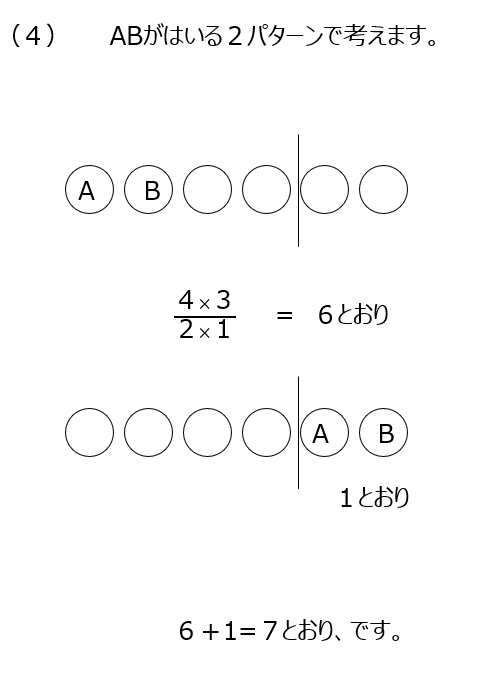
(4)AとBがどちらに居るかを考えます。
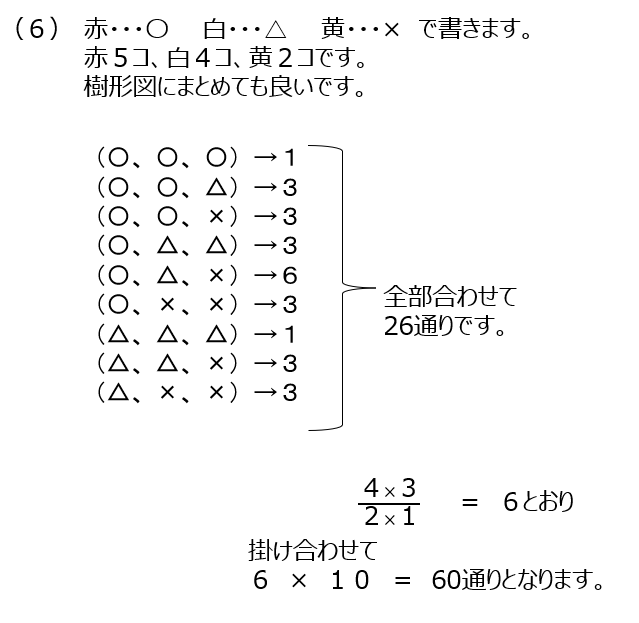
(5)3つのグループに分けます、最後は掛け算になります。
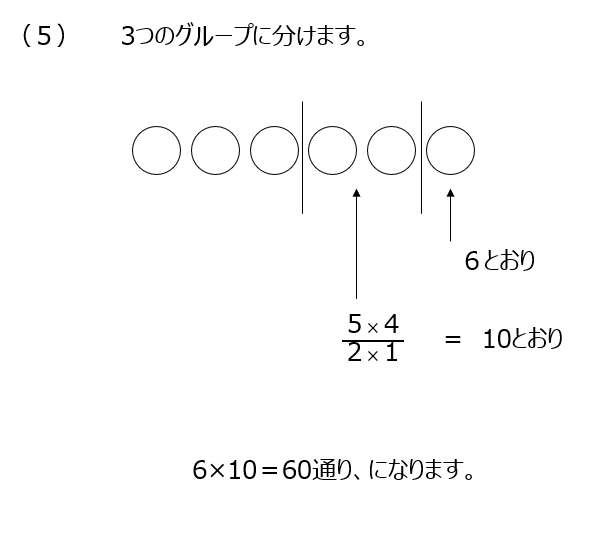
(6)上の(3)と同じ様に書き出したのが動画で紹介されています。樹形樹にしても良いです。計算で解く場合は黄色がもしもう1つあると想定して、解くこともできます。
アプローチ③左1
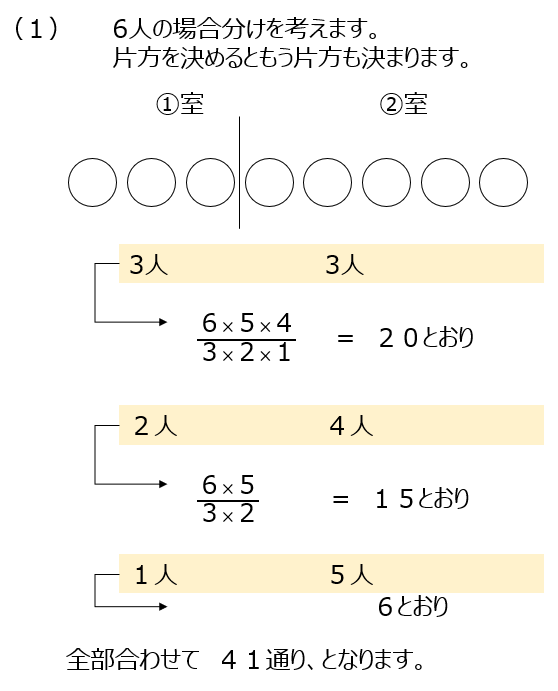
(1)少なくとも1つ以上なので、7-4から3個を配る場合の数にします。3個のパターンを決めて、あとはAとBとCとDがもらうのが何通りかを求めて足します。

(2)サイコロ3回ふって、合計6にします。次は何回か振って6にします。結局は、何通りかを出して、その次に並び替えを考える解き方を動画で説明あります。

アプローチ③右1
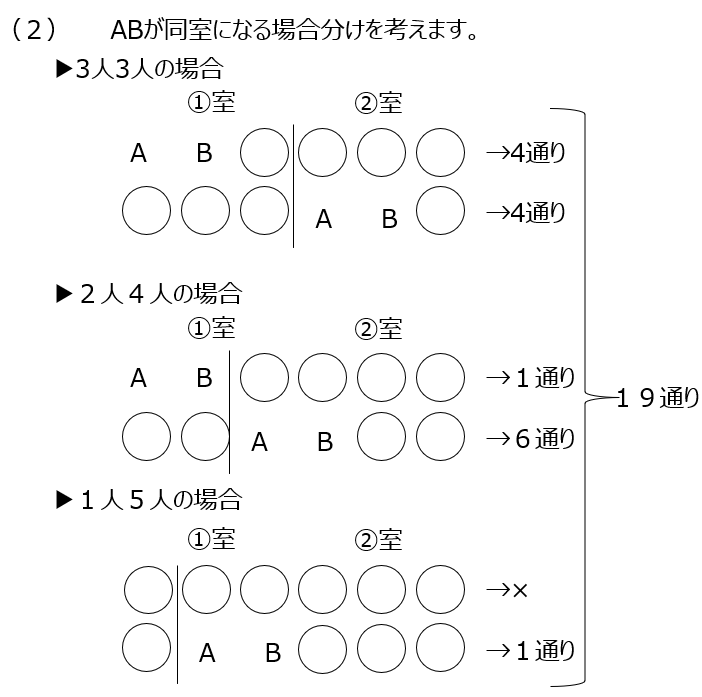
2つの部屋に分けますが、何通りあるか調べて、並び替えがどれだけあるか考えます。次にAとBが同じ部屋になるパターンを、先程の回答を使って考えます。
アプローチ④左1
確からしさの問題です。大中小と違いがあるので、全部では125通りですね。そのうち、6になるのを和分解と並べ替えで求めます。

アプローチ④右1
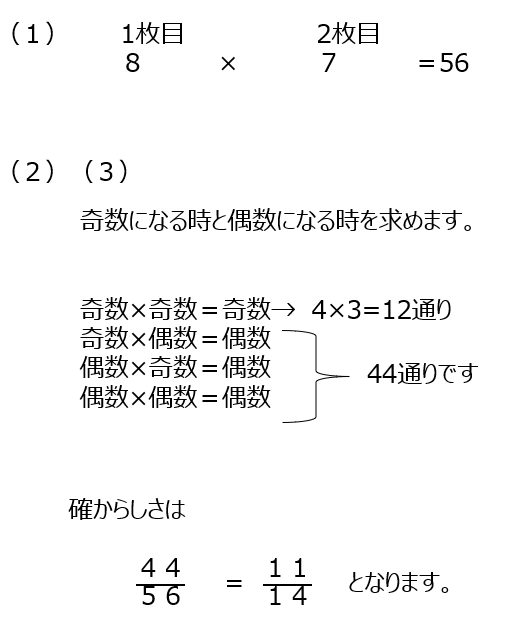
問題文の読み違いに注意が必要な問題です。1枚目と2枚目は区別があります。奇数になる場合を考えて、偶数になるのは全体から引きます。確からしさも、今までの回答を使えば解きやすいです。
アプローチ⑤左A1
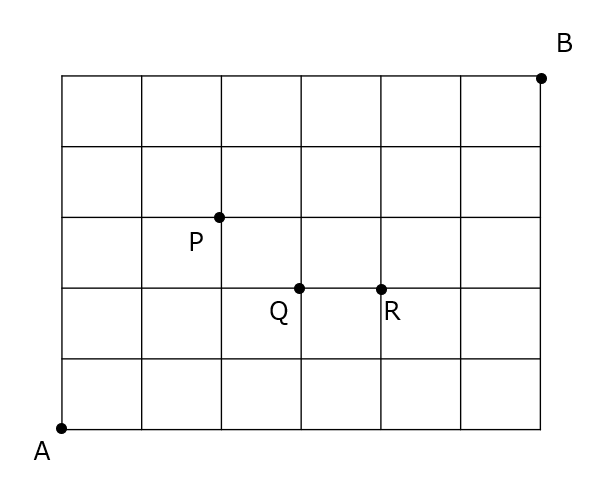
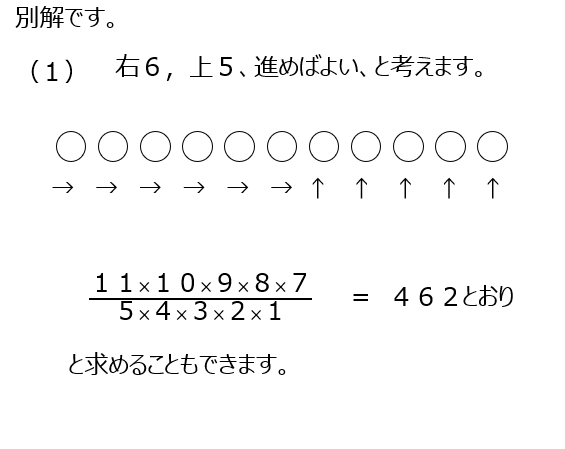
道順の問題です。まずは丁寧に書いて解きます。その後に別解で、計算での解説があります。上に何回、左に何回進むか、と書き出して、場合の数の計算をします。便利ですので、学習しましょう!

アプローチ⑤A右1
家族の並び替えです。父と母をセットにして、父母と母父の両方を考えるのを忘れないようにします。姉と私も、父と母と同じ考え方です。


アプローチ⑤A右2
先程と似てます。AとB、CとDで、入れ替わるパターンを考えて4倍は必要ですよ。考えるときは2つをまとめますが、まとめた中でどうか、を忘れないようにしましょう。


アプローチ⑤B1
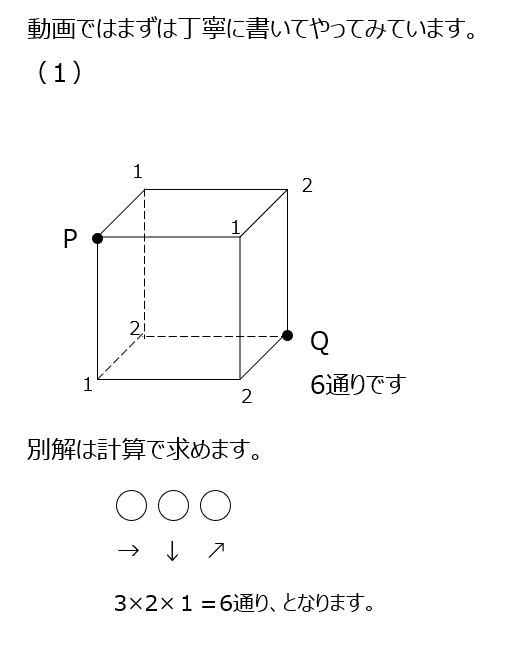
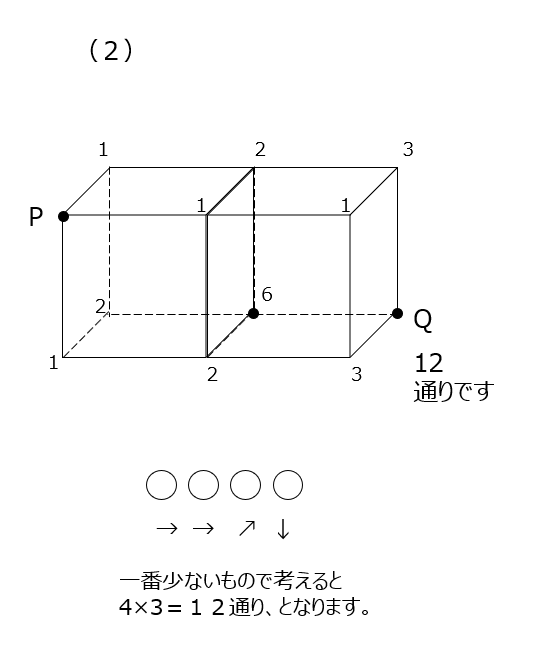
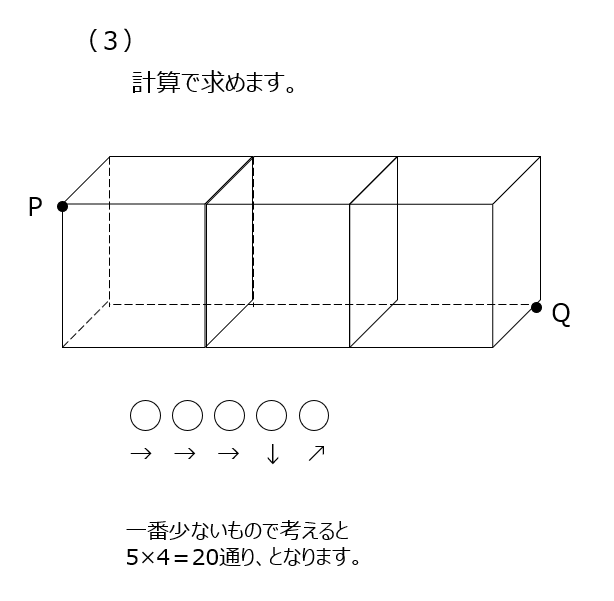
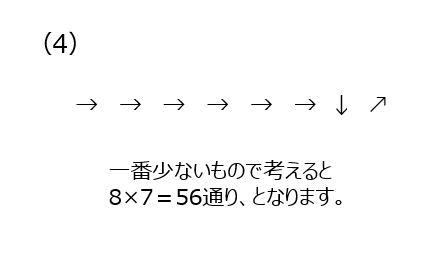
立体の道順です、まずは丁寧に書いて足し上げて解きます。別解では、計算で解きます、目的地までの矢印が何個あるか、と分解して、場合の数の計算をします。このやり方の方が楽ですね。
アプローチ⑥2
問題の確認をして解き進めます。どの道順か、を考えますがセットにして考えます。全体から引く考え方でも進めます。BCもEFも通る道順、重なって数えてしまわないようにしましょう。


アプローチ⑦左1
駅を経由する問題です、遠回り可です。とはいえ、1通りしか無いものもあるので、場合分けして考える必要があります。

アプローチ⑦右1
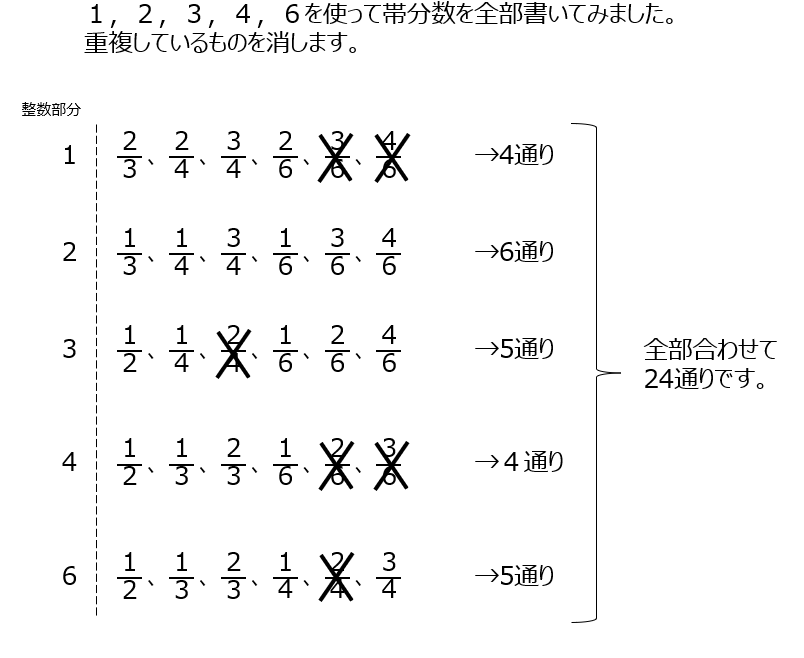
丁寧に書いて作業するだけですが、でもその前に全部で何個あるか計算で求められますか?その後は約分が出来るものを消して進めます。
アプローチ⑧左1
色の塗り分けです、回転させても同じにならない塗り分けを数えます。重複するものを割ります。同じようにな問題が続きますが、動画での図示した説明が分かりやすいですよ。

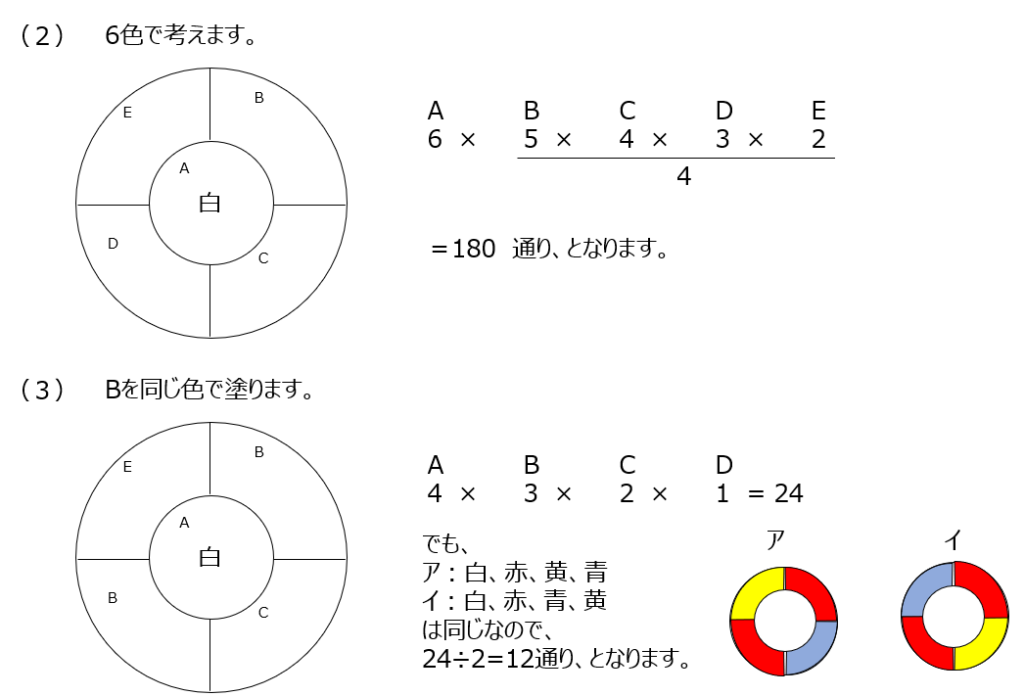
アプローチ⑧左2
(3)のみの解説です。回転させた時にどのパターンが同じか、を考えてその同じパターンの通り数で割ります、これが少しレベル高いですよね、、、
アプローチ⑧右1
全部では何通りかは、わかりますね。次に今までのように、回転させて同じものが何通りかわかるので、それで割ります。で、この問題は最後に反転させた場合、も考えるので、さらに割ります。
まとめ
基本的には何通りかを和分解して、その次に並び替えがある場合はそれを計算します。 ほかにも、同じ並びが何パターンあるかで割り算します。この辺りがなかなかとっつきにくいですが、頑張りましょう。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント