算数の動画「割合」を見ました。
食塩水の濃度や、利益/仕入れ値の計算、ボールの跳ね上がる高さ、など、割合は多岐にわたって出題されますよ、分かりにくい問題は図に書いて考えていくようにしましょう。

6年生のこの時期に克服しておきたい単元ですね
導入と基本③3⃣
跳ね上がる高さを求めます。はじめを1として考えてみましょう。
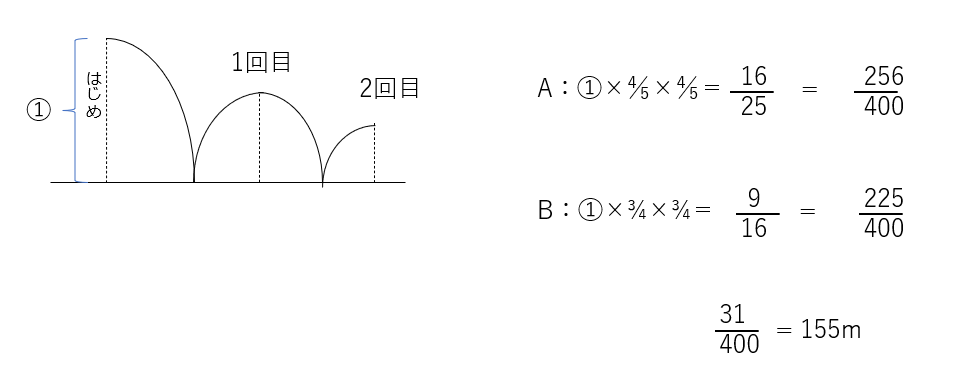
導入と基本③4⃣
Aの3回目とBの2回目が同じ高さ、です。同じ高さとのところを①として考えましょう。(Aのはじめ)×½×½×½=⓵、と置けます。
Aは①÷½÷½÷½=⑧となります。Bも同じ様に、①÷⅓÷⅓=⑨、となります。この差①が9mなので、Aのはじめの高さ⑧は9x⑧=72m、となります。
※導入と基本③4⃣と同じ問題で、数値設定がやや複雑になった問題がアプローチ③右1⃣(2)に乗っています。時間のある人は解いてみましょう(解説動画はありません)
アプローチ①左1⃣
仕入れ値からの売り上げを考えます、図に書いて解いていきましょう。⅓は4割増し、⅔は2割5分増し、なので、全体に③で仕入れたとします。

別解は平均算での考え方です。
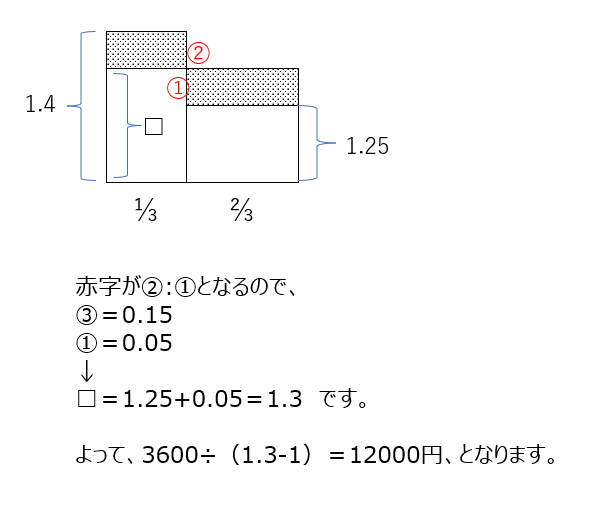
アプローチ①右1⃣
面積の比から、長さの比を求めて考えます。白と黄の縦の比は2:5、赤と青の縦の比は3:5なので、これを7と8の最小公倍数でそろえると、16:40、21:35となります。これから、白と赤の面積比は3:28、縦の比は16:21なので、横の比は割り算で求まります、簡単にすると9:64となります。
アプローチ②左1⃣
食塩水の問題です、受け渡しをする時の食塩の量に気を付けて考えていきます。遷移図を書いて解きましょう。
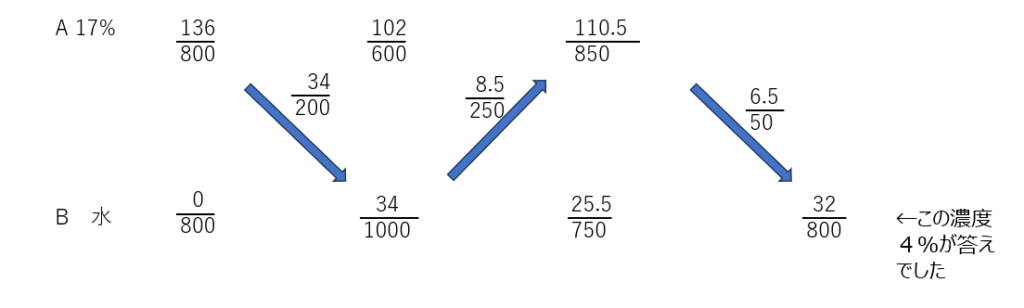
アプローチ②右1⃣
食塩水を交換するときに、食塩水の量と食塩量を考えて解きます。解法1では遷移図で解きます。混ぜて同じ濃度になるということは、最初のAとBを混ぜても同じ濃度になります。また、100g交換すると、8gの塩の量がずれるので、19.2gずれるには240gの交換が必要、とわかります。解法2では平均算で解きます、図を書いて考えましょう。動画の説明は分かりやすいです。上級者向けの補足では、混ぜた量の比から考えて進めていきます、、なかなかの難易度ですね。
アプローチ③左1⃣
3回目がの跳ね上がる高さがおなじですので①とします。Aが¾、BはAの⅘倍なので、⅗、となります。Aの3回目から考えると、①÷¾÷¾÷¾、Bの3回目から考えると、①÷⅗÷⅗÷⅗、です。この計算から答えを求めます。
アプローチ④左1⃣
利益は売り上げから仕入れの値の合計を引いたものです、という基本を押さえて解きましょう。何を求められているかをきちんと問題も読みます。
仕入れ1個を1、とすると、1×100=100が仕入れ値です。定価(2割5分増し)で売れたものは、1.25×70個で87.5です、8個は売れなかったので、売り上げゼロです。定価の0.9倍で売れたものは1.25×0.9×22コ=24¾、なので、全部合わせると、112¼、となります。このうち、利益3920円は12¼なので、割り算にて仕入れ1,が求まりますが、定価を聞かれているので間違えないようにしましょう。
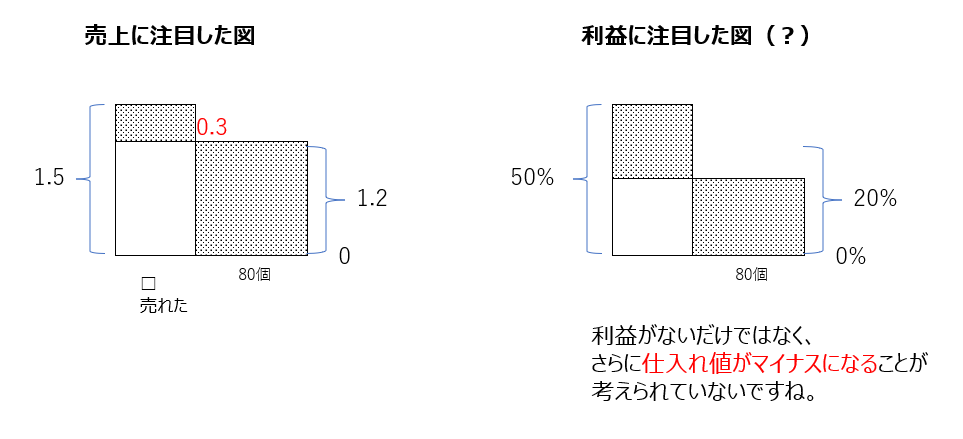
アプローチ④右1⃣
売り上げに注目した図、で考えると正しく解けます。利益に注目した図で考えると、考慮(利益が無いだけではなく、仕入れ値がマイナスになることを考える)が必要になるので、気を付けましょう。
アプローチ⑤左1⃣
表に書いてまとめながら、比をそろえて解き進めます。最初に昨年の男女比と合計の比をそろえて、次に今年の合計と計を30で揃えます。ここまで書けると残りの問題が解きやすいですね。
| 男 | 女 | 計 | |
|---|---|---|---|
| 昨年 | 15 | 9 | 24 |
| 新入 | 5 | 1 | 6 |
| 今年合計 | 20 | 10 | 30 |
アプローチ⑤右1⃣
合格と不合格の合計が受験者の総数、になります。比をそろえて進めましょう。受験者の男子を72として比をそろえます。
| 男 | 女 | 計 | |
|---|---|---|---|
| 合格 | 27 | 15 | 42 |
| 不合格 | 45 | 49 | 94 |
| 受験者(計) | 72 | 64 | 136 |
アプローチ⑥右1⃣
仮に、20個が全部売れたとして、で考えると、解けますね、テクニックも覚えましょう。
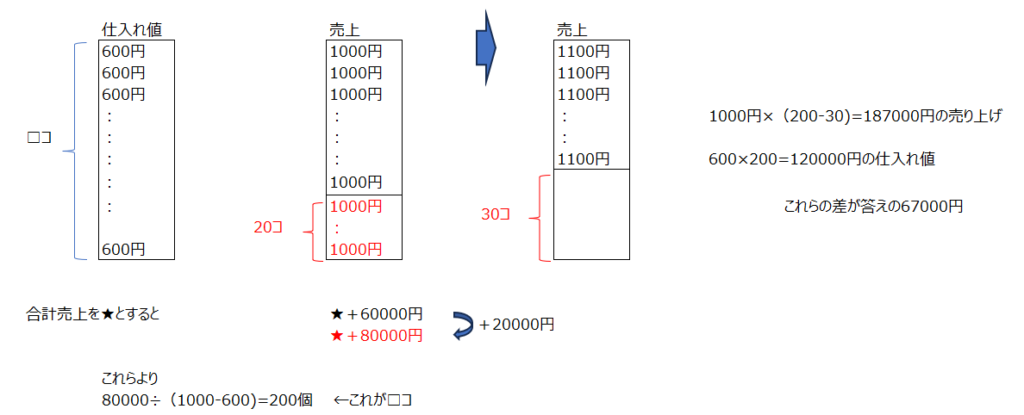
アプローチ⑦左1⃣
食塩水を水に加えていきます、比で考えます。どんどん薄くなっていきます。はじめの食塩水の濃度を1とすると、試験管1つめは、濃度は⅓になります、2つ目の試験管は、12分の1になります、最後は60分の1まで薄まります。これが0.3%なので、最初の1が18%、と求まります。
アプローチ⑦右1⃣
食塩水をA,B,Cでやり取りして進めます、遷移図に書いて解いていきましょう。最後のCの食塩の量を①、とおくと、紐解けていきます。ややこしい遷移でもありますが、動画では丁寧に説明があるので、分からない人か是非確認しておきましょう。
アプローチ⑧左1⃣
昨年の値段Aを①として解いていきます。比を出した後に、比の計算までできるようにしましょう。
昨年は、Aは①、Bは①+200円、Cは①+400円、これに、今年お倍率を掛けて、Aは1.3、Bは1.2+230円、Cは1.1+440円、となります。昨年の合計は③+600円、今年は3.6+680円、で、この比が60:71となります。
アプローチ⑧右1⃣
跳ね返りが80%です、段々になっているので、どこからが跳ね返えりが80%なのか、をきちんと確認して進めましょう。二回目の跳ね返る高さは、50cm引いたものから⅘倍、となります。
実戦編B1⃣
問題文がややこしいので、きちんと読んで理解しましょう。利益が同じ、です。
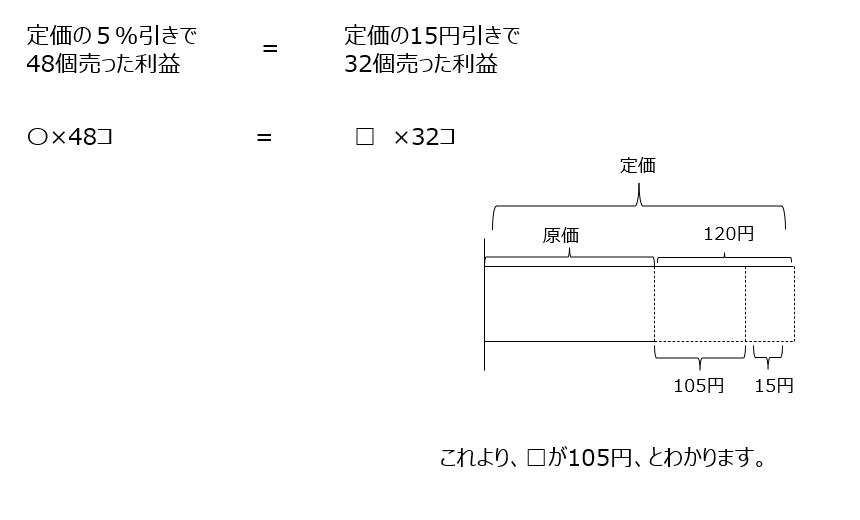
実戦編B3⃣
消去算でとけますよ。式を2つ書いてみましょう。ただ、問題は、Aを買った値段を聞かれています。
Aが1割7分引き、Bが1割1分引き、なので、Aを〇、Bを□、とすると、〇0.83+□0.89==51780円、と出せます。また、全体で1割3分7厘引きでも51780円なので、51780÷(1-0.137)=60000円、で、これは〇1+□1=60000円です。この2つから消去算をしましょう。
今週の立体切断1⃣
今日から2回切断になります、今回の動画の(1)は、まだ1回切断です。動画では、重なった体積を引く方法で丁寧に説明がありますので、苦手な人は参考にしましょう。
まとめ
割合は、算数のどの問題でも出てきますね、もちろん理科でも。。。小学5年で一番重要な単元、とも聞いたことありますが、6年生になってまさしくその通りな感じです。苦手な考え方は、繰り返し解いて、身につけましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント