算数の動画「平面図形(3)」を見ました。
夏期講習3回目となります、補助線をどう引いて考えるか、の問題が多くあります。引き方も何種類かあり、動画では複数の解法を分かりやすく説明してくれています。砂時計とピラミッド型の相似、内部底辺、など解くための基本をおさえましょう。

「ひらめき」が無くても、多数の問題を解いて、経験でカバーしたいです!!
導入と基本①4⃣
面積と高さがと同じなら、底辺も同じです。この問題は、面積の比が変わりますが高さは同じ三角形を探して解きます。
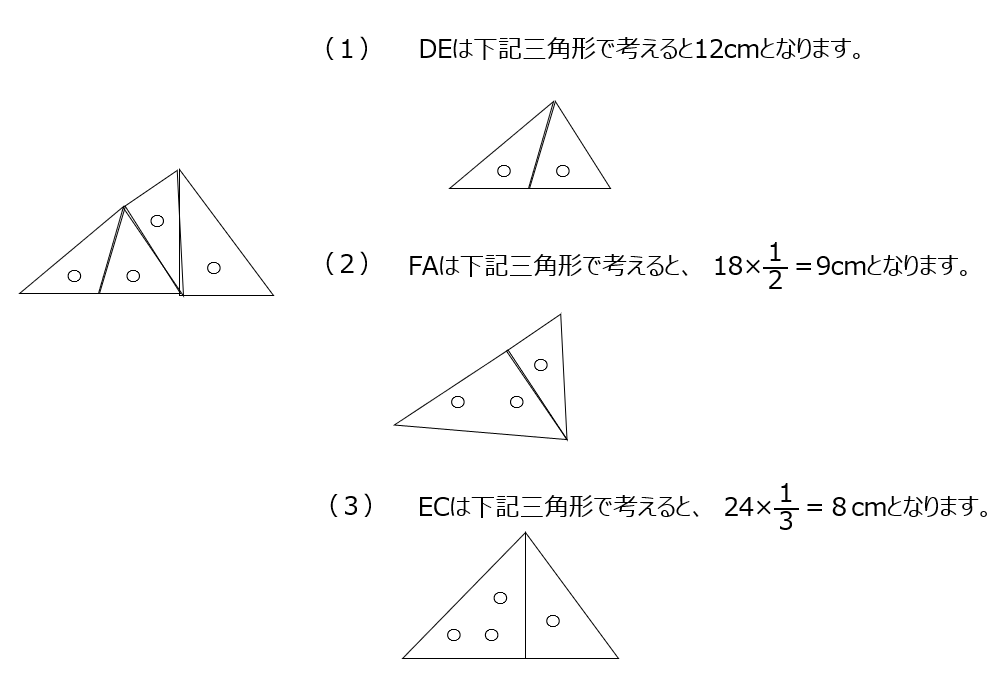
導入と基本②2⃣
高さが無いので比で考えます。台形の面積を8として全体を3と1と4の三角形に分けます。
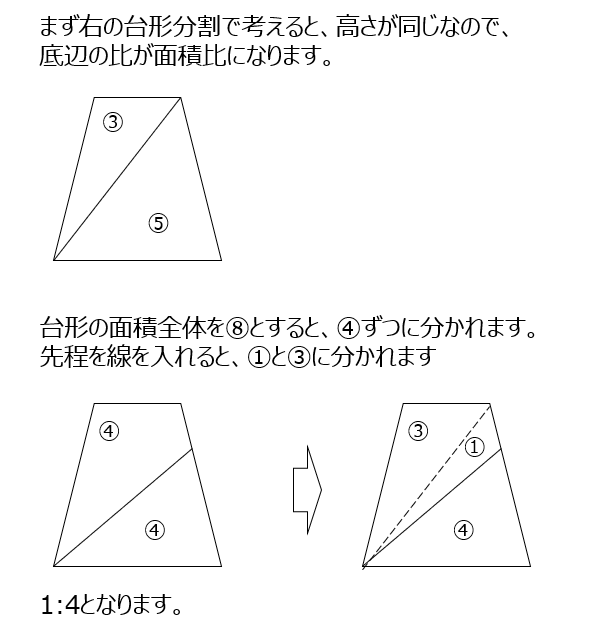
アプローチ①1⃣
(1)砂時計とピラミッドの相似を使って、求める台形の上底と下底を出します。
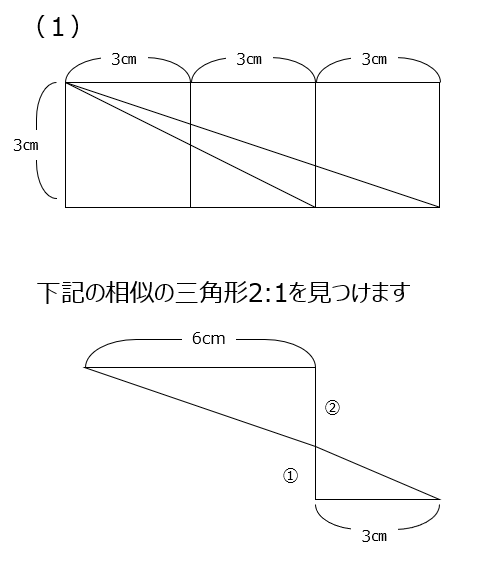
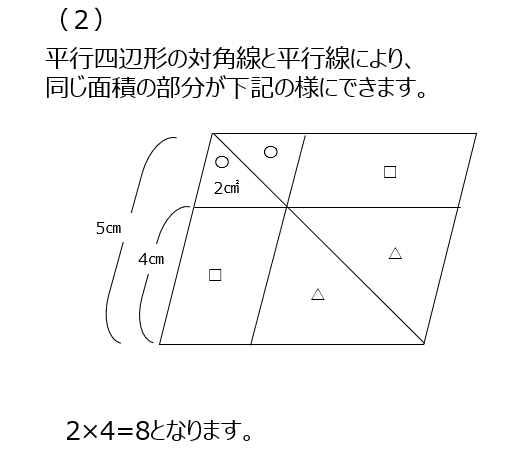
(2)平行四辺形の対角線は面積を二等分します。
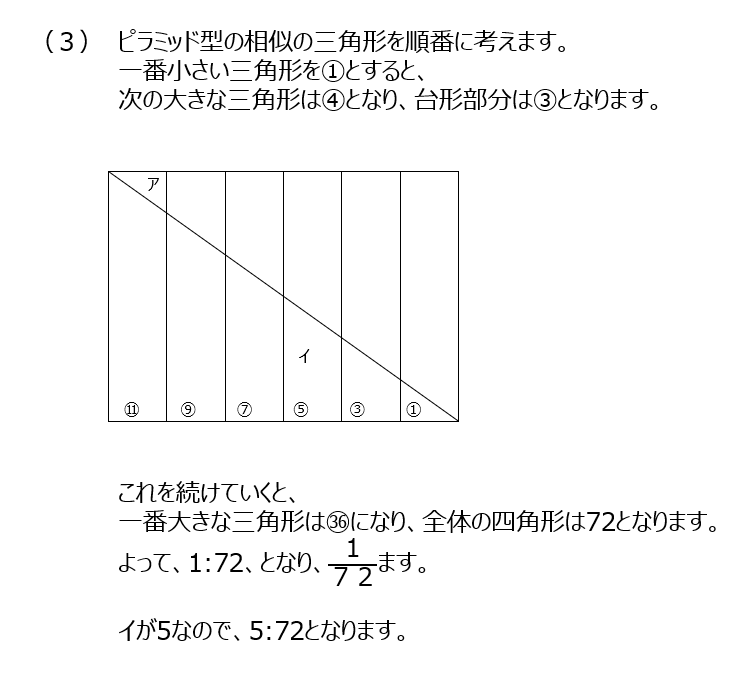
(3)相似がたくさんあります、1番小さい三角形を1として全体の割合を出します。
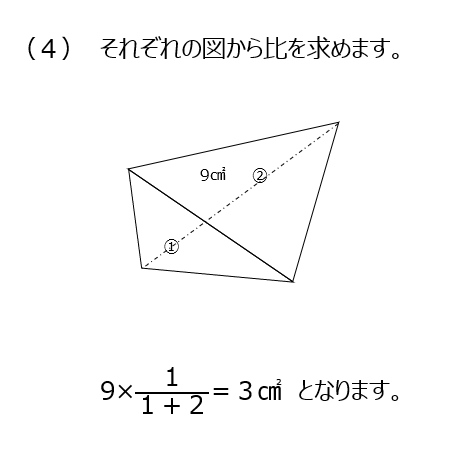
(4)対角線を引いて内部底辺の考え方から解きます。
アプローチ②1⃣
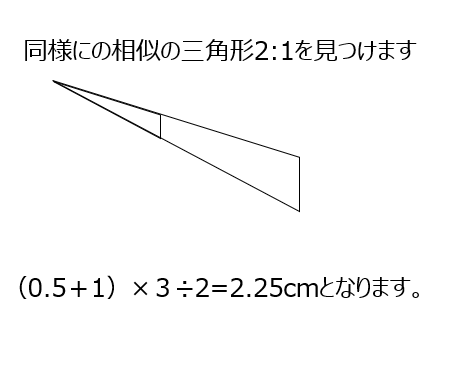
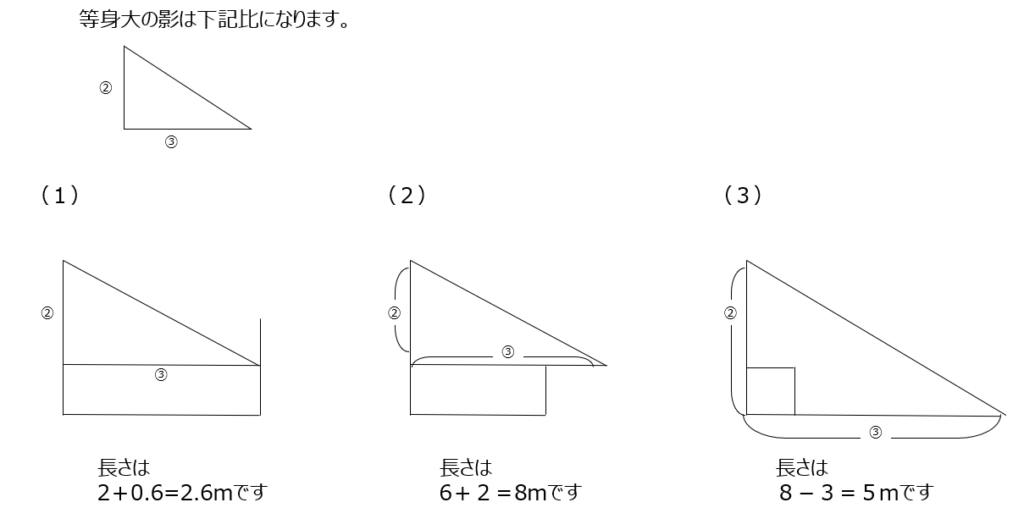
木の影が出来る問題です。2:3の直角三角形の相似を使って解きます。
アプローチ③A1⃣
正三角形の性質を使います。60度をはさんで、2:1になります、覚えておきましょう!円の中心から線で区切ってみるのが解き方になりめすよ。
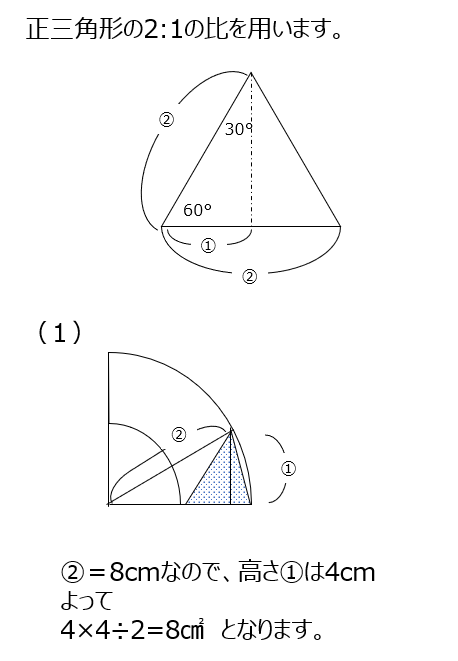

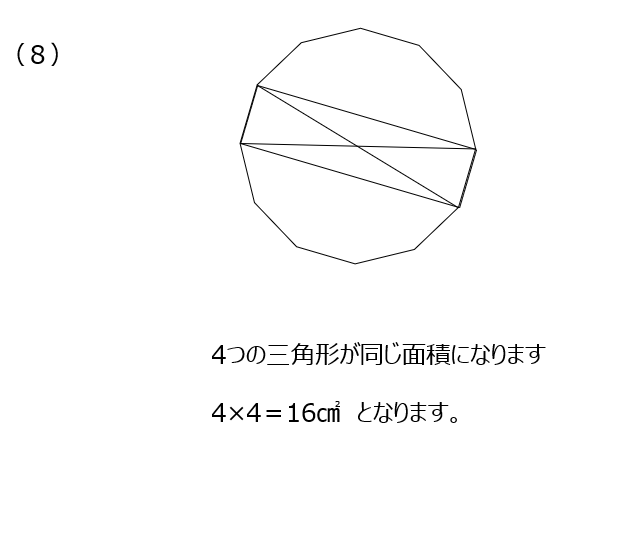
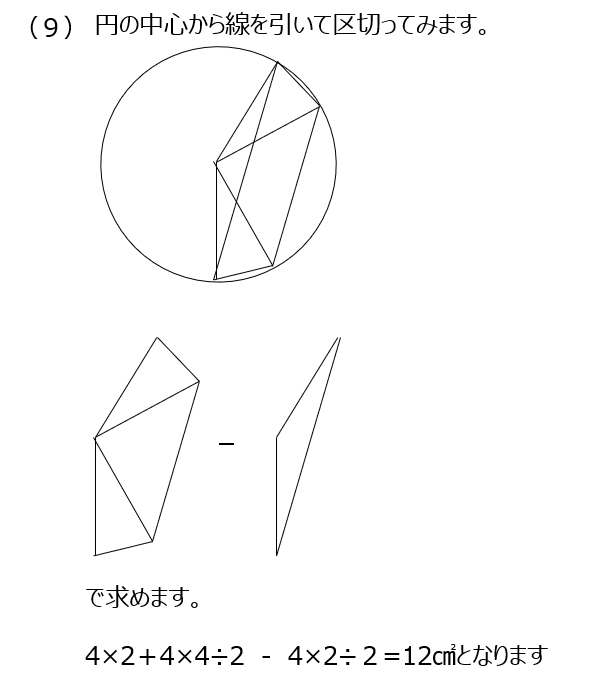
アプローチ③B1⃣
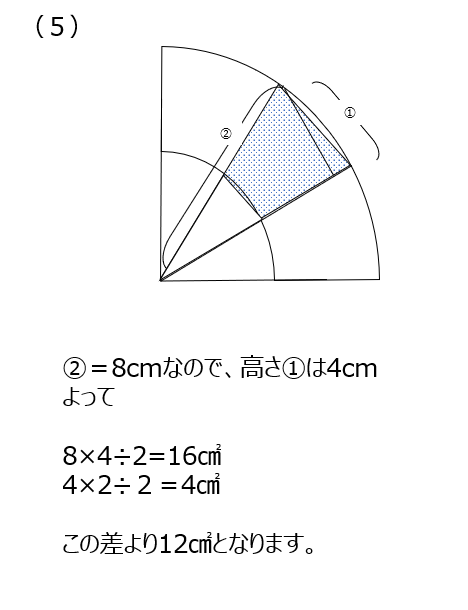
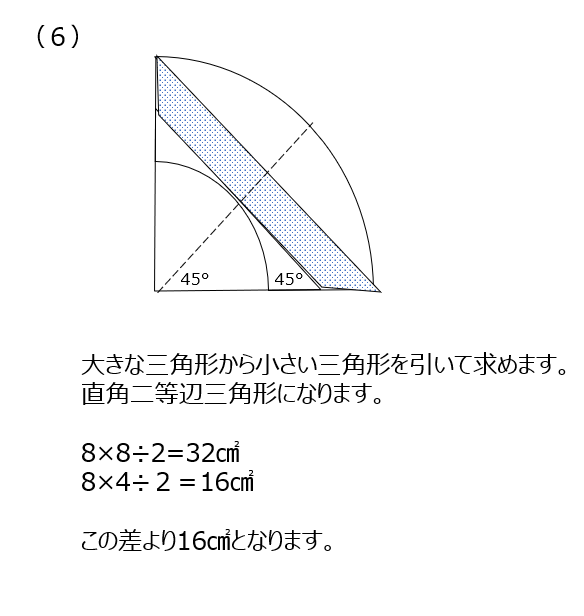
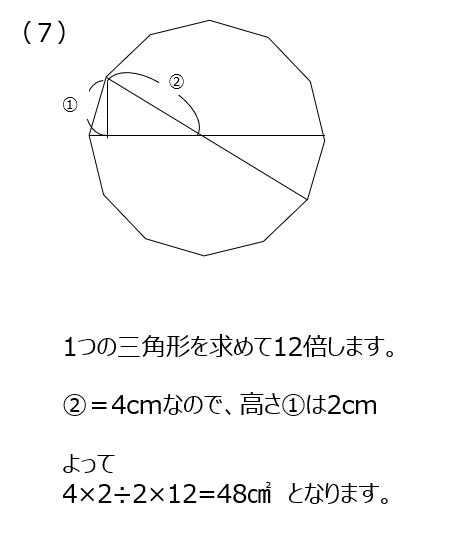
この問題も中心から線を引いて区切って考えます。150°が出てきているので、正三角形で考えます。(1)と(2)が実は同じ面積です。(3)では図形の式を書いてみます、三角形の面積が同じなので、おうぎ型を合わせたものが求める面積になります。(4)でも図形の式から、おうぎ型の面積を出すことになります。
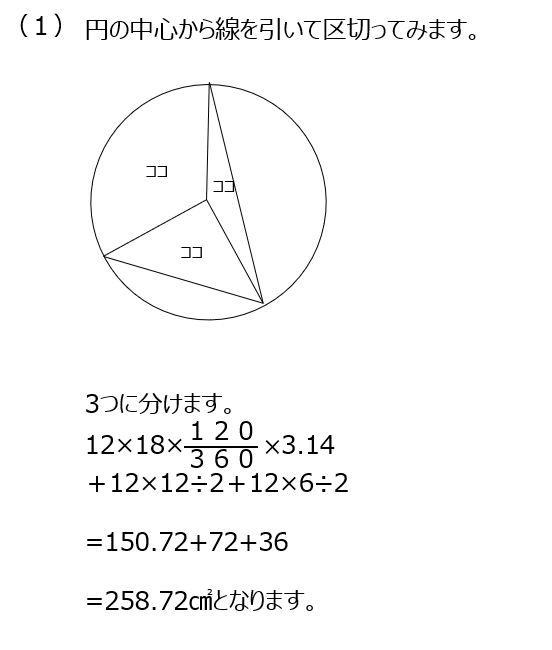

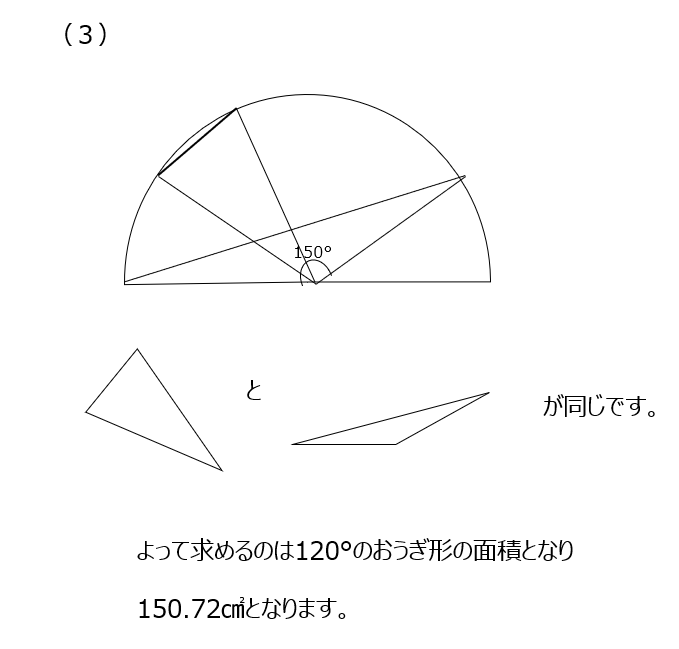
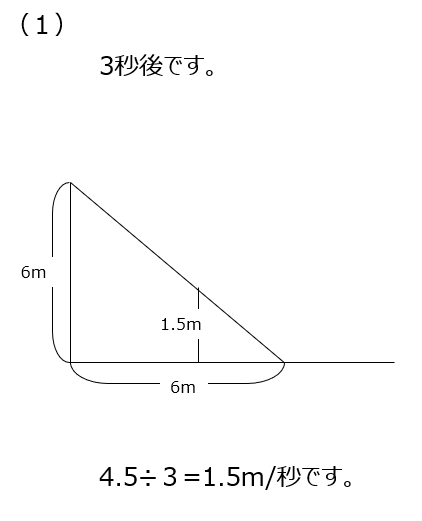
アプローチ④左1⃣
等身大の影、とは、身長と影が同じ長さなので1:1ですね。図に書いて解き進めましょう。
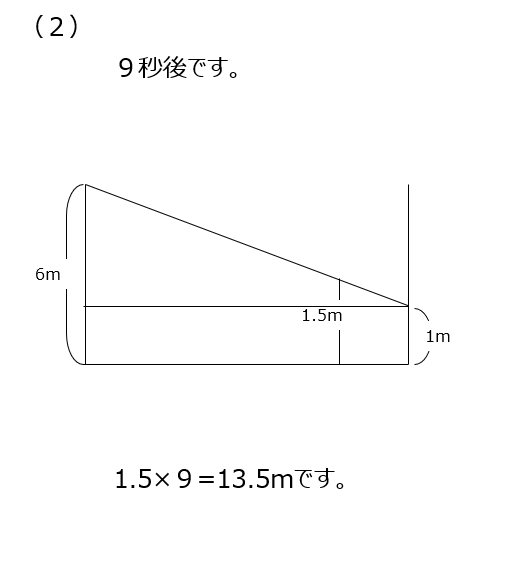
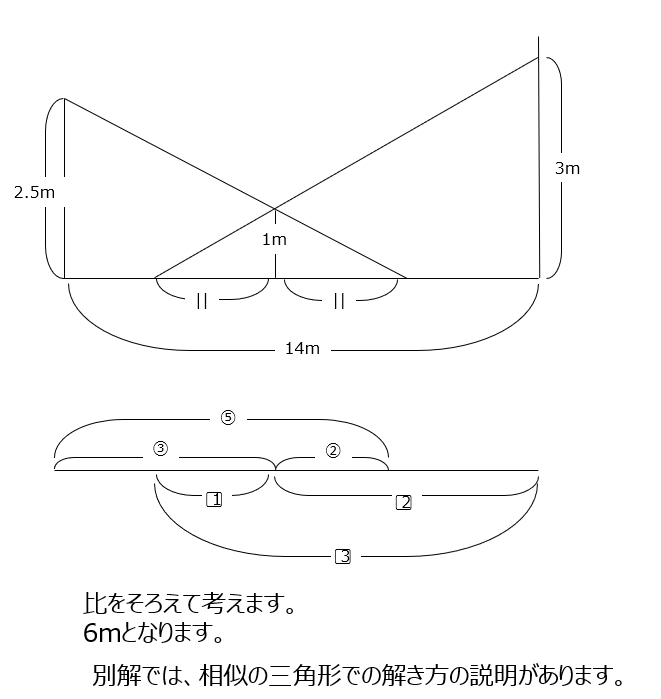
アプローチ④右2⃣
三角形が重なっています。ピラミッド型の相似の三角形で比を求めて、同じ比に揃えで解きます。別解では、この問題では使えるやり方の説明があります、いろいろな解き方に触れておきましょう。
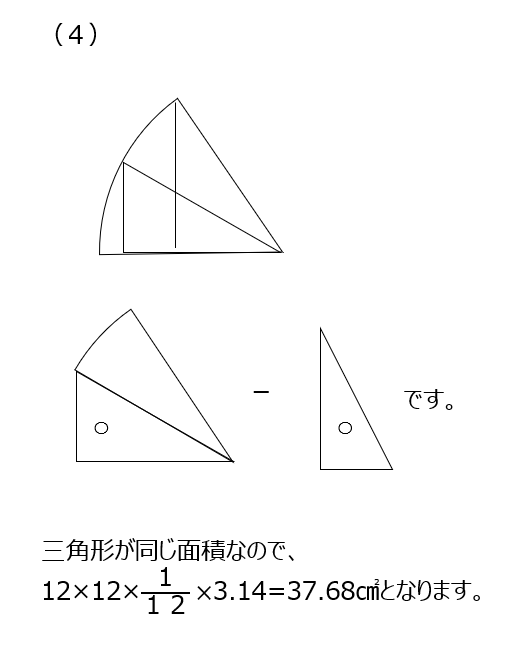
アプローチ⑤左1⃣
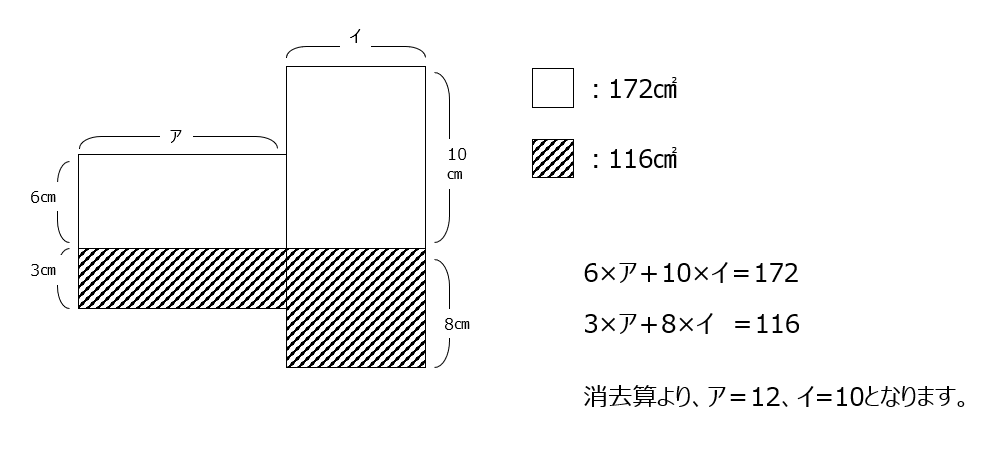
アとイで式が二つできるので消去算になります。最小公倍数にしなくとも、片方の式を2で割るとアを消すことができますので、工夫してこなしましょう。
アプローチ⑤右1⃣
解法1では、補助線を引いて底辺の比で三角形の面積比を出して、消去算で求めます。
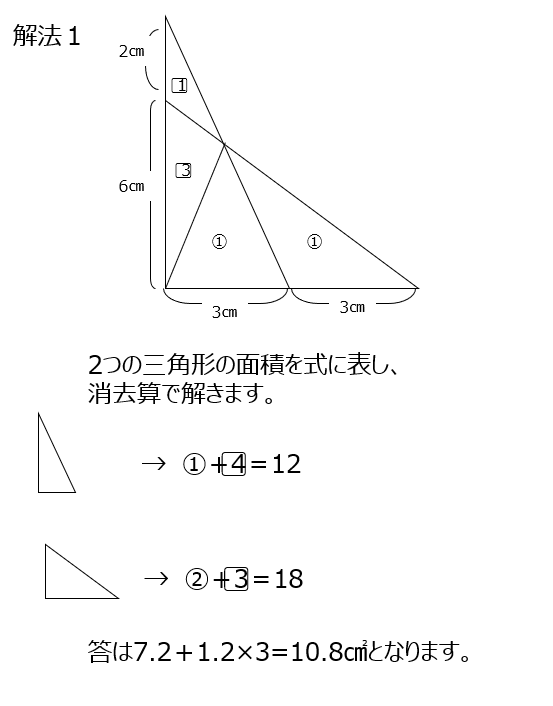
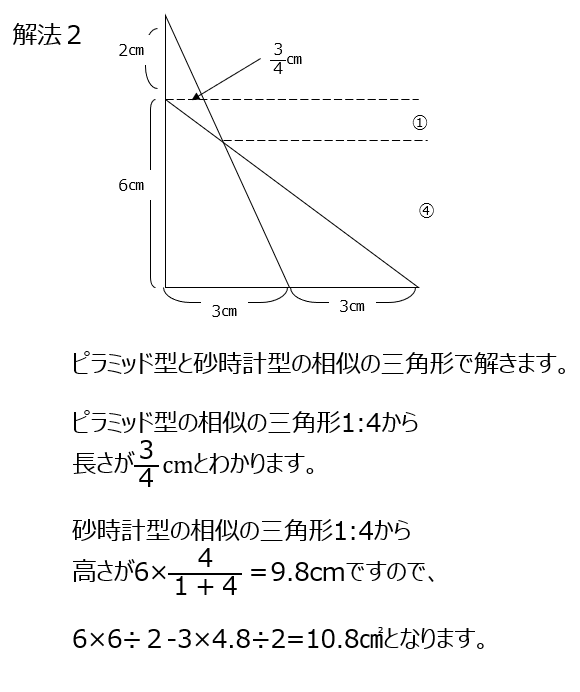
解法2では、別の場所に補助線を引いて、ピラミッド型と砂時計型の相似の三角形を使って解きます。
アプローチ⑥左1⃣
既に書いてある三角形に沿って補助線を引いて、求める三角形を分けます。最小公倍数の何倍か、で、底辺や高さを求めます。
アプローチ⑥右1⃣
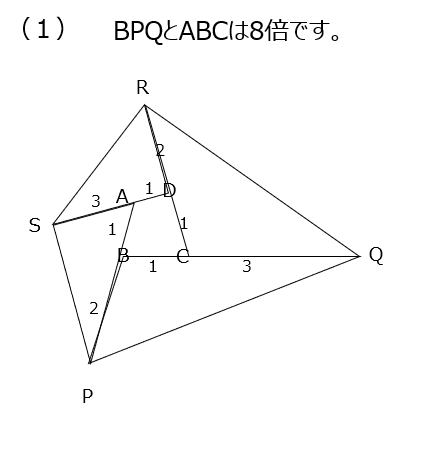
各辺を何倍かに伸ばして大きな三角形ができてきます。比で比べて解くのは5年生のときに学びましたね、ただ、中心にあるのは四角形なので、途中の問題は三角形との比較でしたが、その辺りが注意ですね。
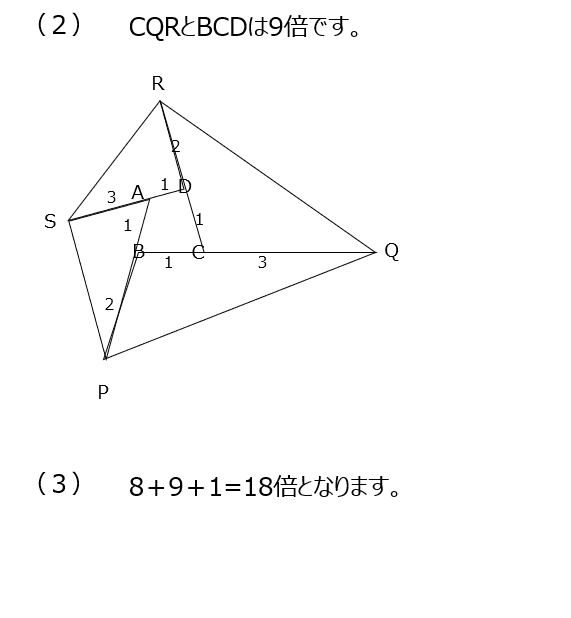
アプローチ⑦A1⃣
中心から線を引いて区切ります。おうぎ型を6つから正三角形2つを引く計算になりますが、動画で説明があります。
アプローチ⑦B1⃣
解法1では、求める斜線部を4等分し、その一つを求めて解きます。
解法2では、斜線部に正方形を書いて、求めますが、解法1と2では近似値を用いて解いているので答えが変わってきます。
アプローチ⑧左1⃣
ひし形を重ねた図形です。4等分して、そのひとつで考えます。補助線を引いて、求めます。動画で詳しく説明がありますので、わからない人は参照しましょう。
アプローチ⑧右1⃣
おうぎ型を取り除いた図で動画では説明があります。補助線を引いて三角形を分割して解きます。
まとめ
補助線を引いて三角形を分割したり、相似の三角形を求めたりして求めます。3回目になると、解く時に工夫がたくさん必要になりますね。解法もたくさん理解して、いろんな視点で考えられるチカラをつけたいですね^ ^
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント