算数の動画「推理と論証」を見ました。
論理的に考える問題を学習します。推理なのでクイズの要素もあり、考えることが好きな子供は楽しく取り組めそうな単元です。きちんと筋道立てての考え方の基本なので、全教科に関連しそうな内容です、楽しみながら解いていきましょう!

好き嫌いが、はっきり分かれる単元ですかね~
アプローチ①左1⃣
Aが決まれば、B、C、Gが決まりますね。確定したものだけを書き込んでいきましょう。動画では、あり得ない配置に×をつけて分かりやすくしていますね。

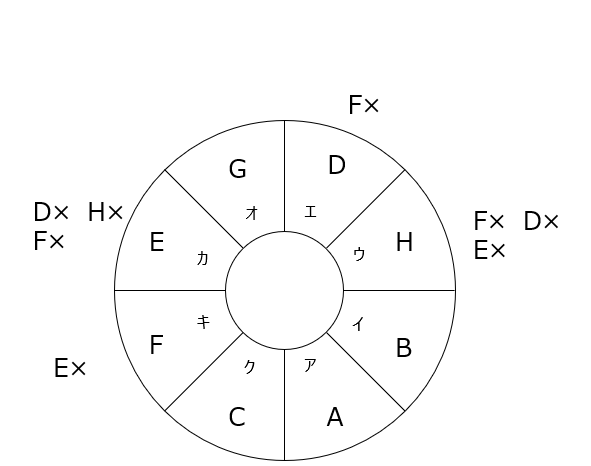
アプローチ①右1⃣
順位を当てます。でも、誰かがウソをついています。A、B、Cがそれぞれウソをついていた場合、として仮定して解き進めます。
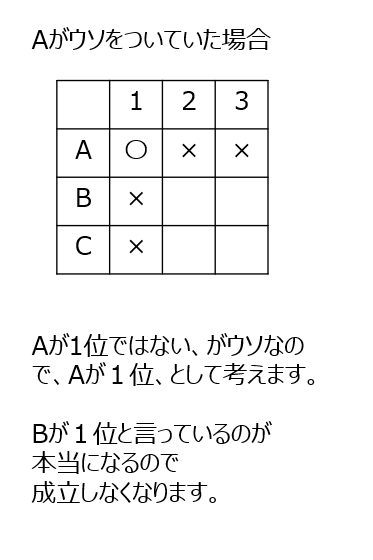
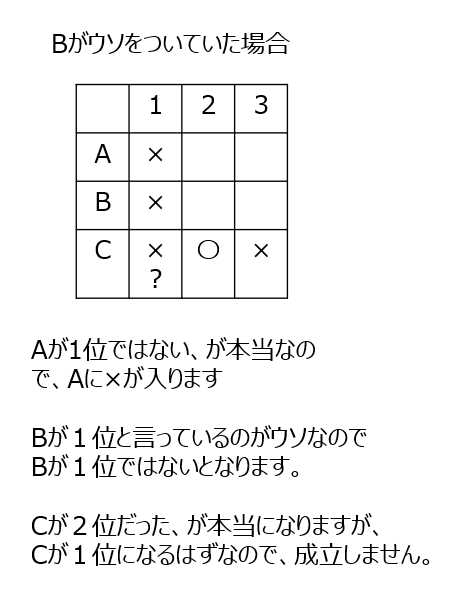
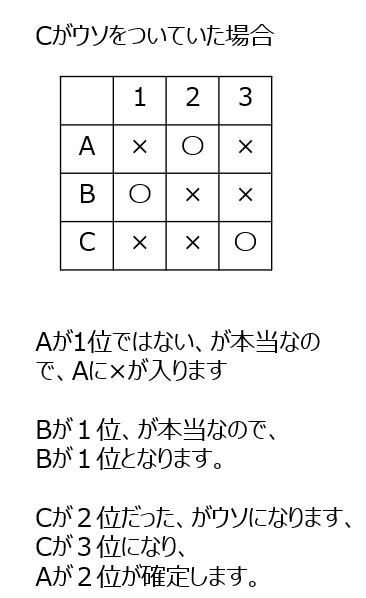
アプローチ②左2⃣
順位の予想の問題です。確定している事を書き込みます。1人の順位がわかったら、他の人の予想も消しておく事を忘れないようにしましょう。
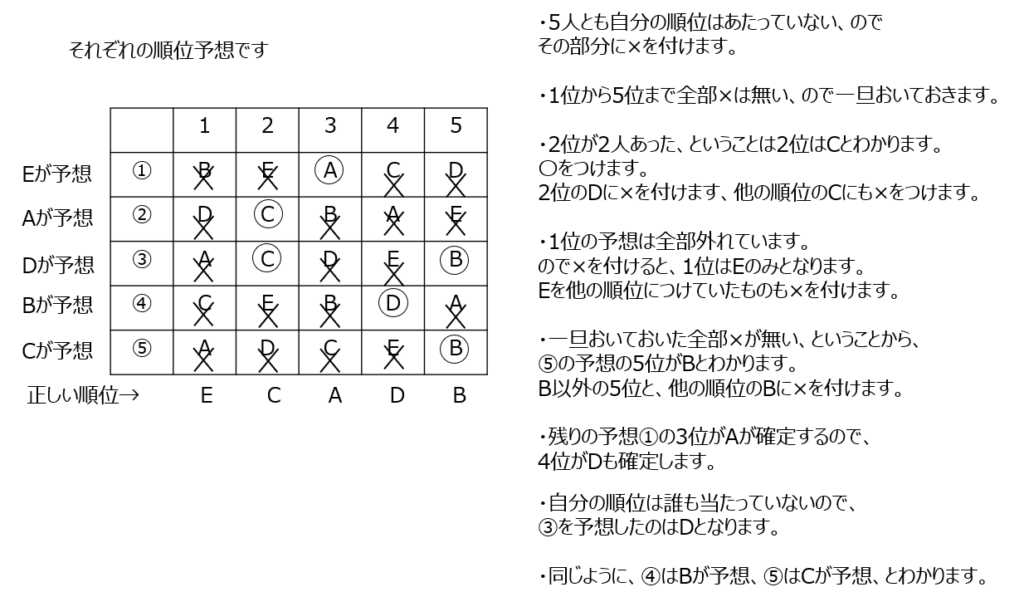
アプローチ②右1⃣
4チームがそれぞれ2回ずつ戦う問題です。最後にふた通りが残るのでそれぞれのパターンで考えてみます。
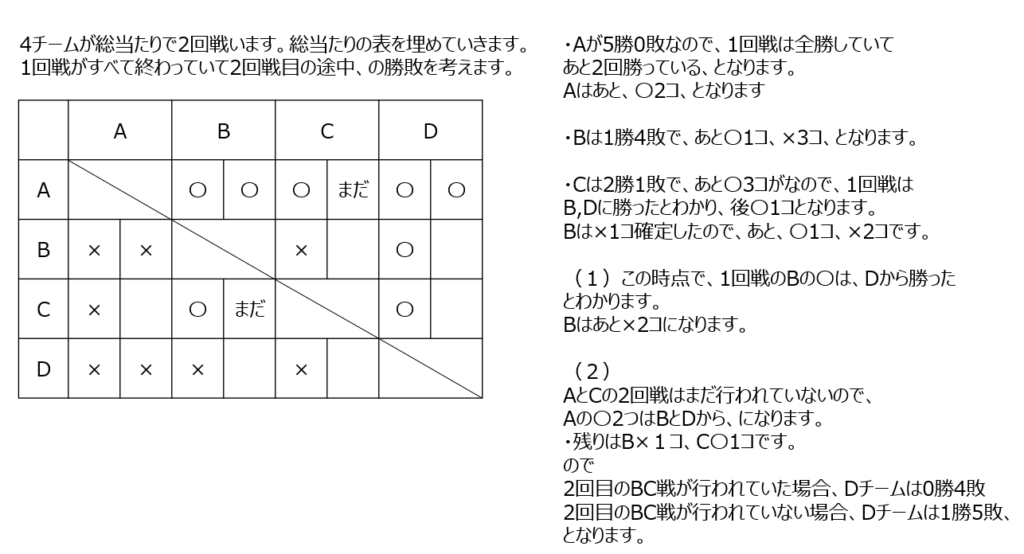
アプローチ③左1⃣
得点、最高点、平均点の問題です。考えられる最高合計点、最低合計点から平均点をだし、その範囲に無いものは答えから外れます。残ったもののうち、5で割った時の小数点を考えると答えが分かります。なかなか面白い考え方ですね。

アプローチ③右2⃣
サイコロの大小の合計の問題です。大のサイコロが4の倍数なので、場合分けして考えて解きます。

アプローチ④左2⃣
カードに書かれている数を当てます。最も質問を少なくして当てます。なるべく均等になるような質問をしていきます。動画では図示しての説明があり、わかりやすいですね。
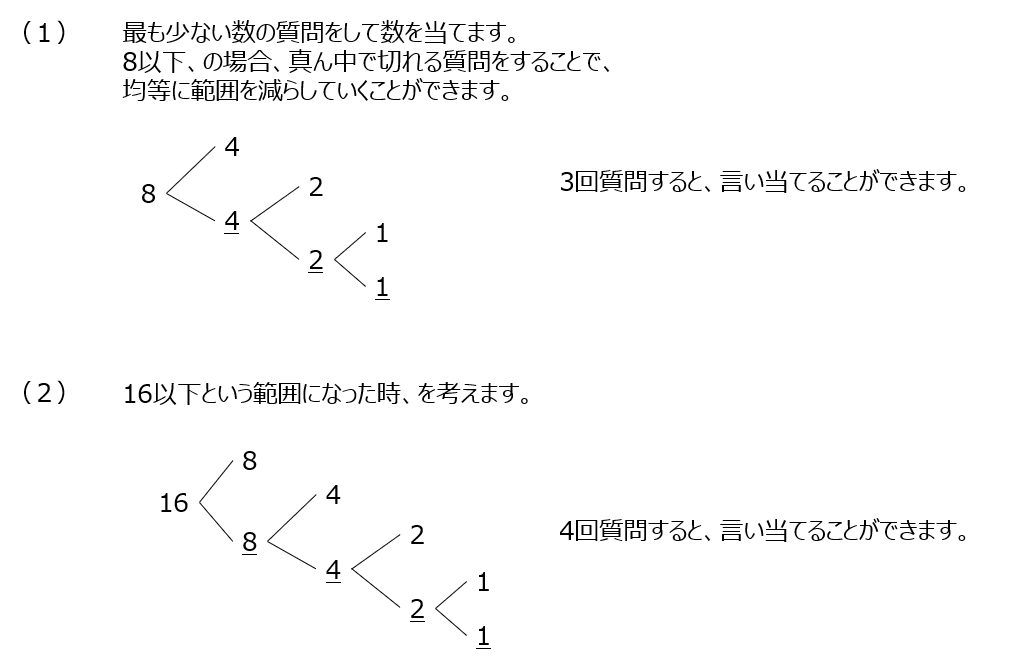

アプローチ④右1⃣
重さの違う球をてんびんに乗せて見つけます。まずはじめに、として、動画では考え方の説明があります。3個の場合、10個の場合での説明となりますが、3つの均等なグループに分けて考えていく、というのが大方針になります。この方針が分かれば問題は解けますね。
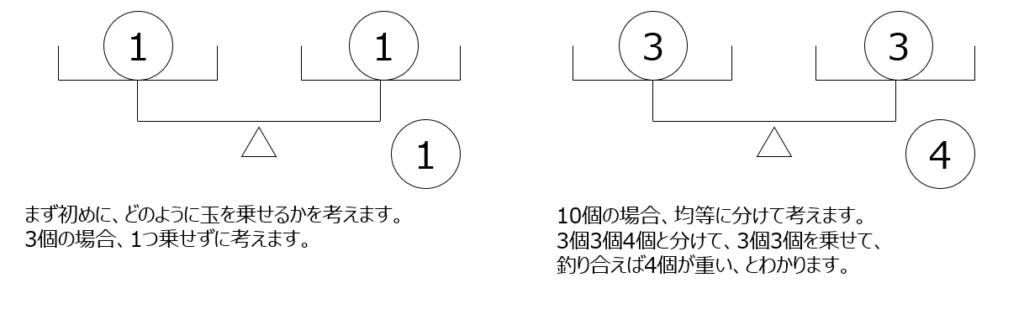


アプローチ⑤1⃣
各チームの総得失点とトーナメント表があります。わかってるところから埋めていきますが、勝ち進んだかどうか、まで考えて進めます。
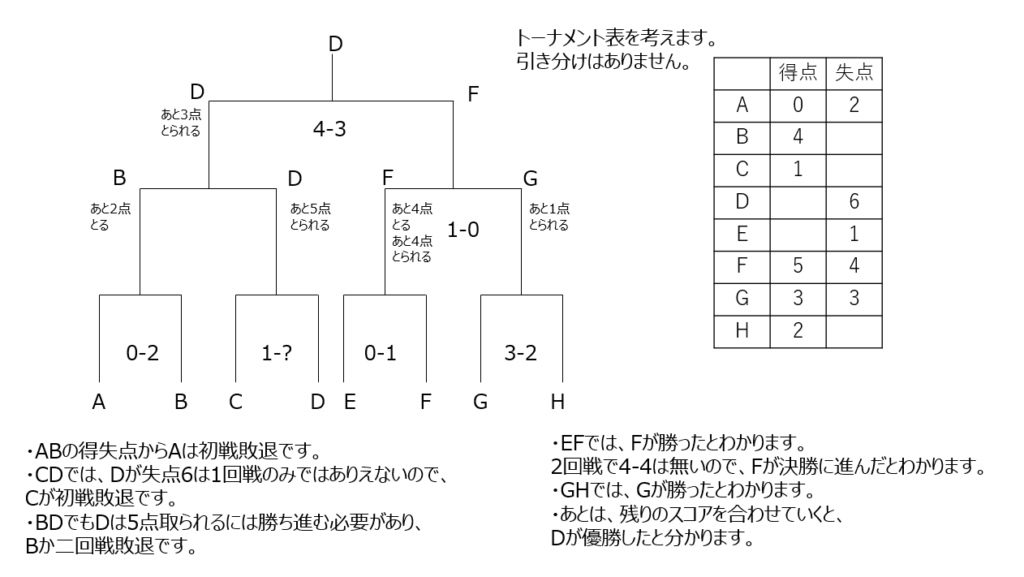
アプローチ⑥左1⃣
てんびんからどの玉か重いか、を考えます。軽くない球はどれか、を考えて進めます。
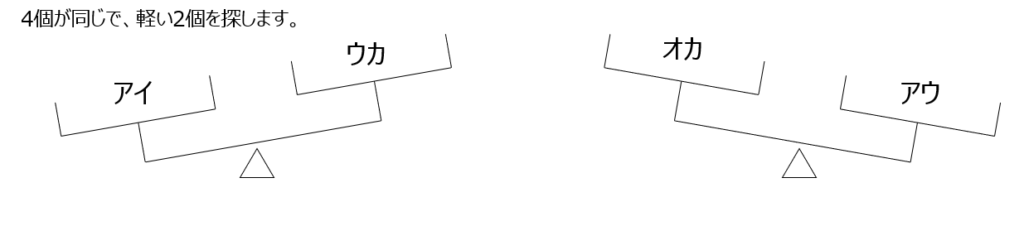

アプローチ⑥右1⃣
条件から重さを考えます。B+Aはちょうど半分、B+Dは半分より重いのて、D>Aとなります。同じようにB>Cとなります。これらから、何通りかを求めます。

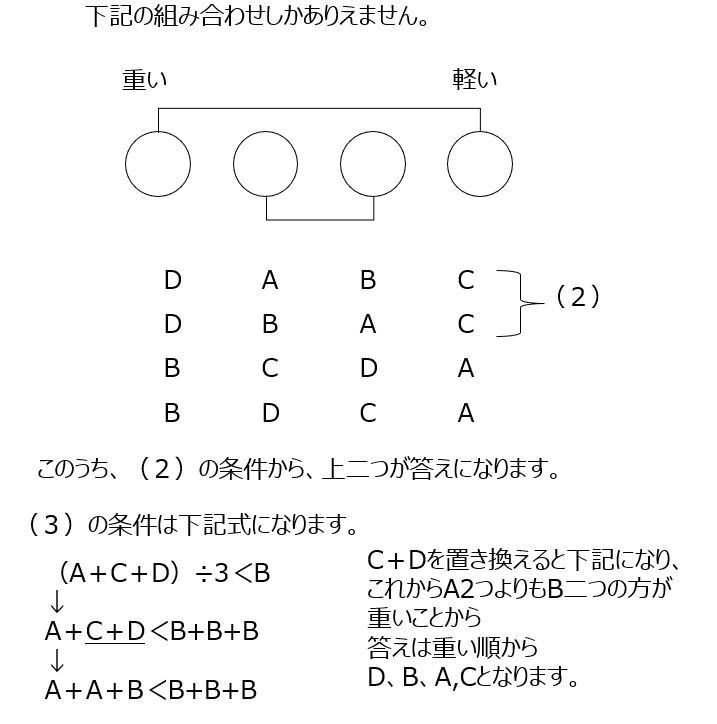
アプローチ⑦左2⃣
4×4の試合の表です。条件から確定する部分から埋めていきます。かたき討ち、のルールがあります。
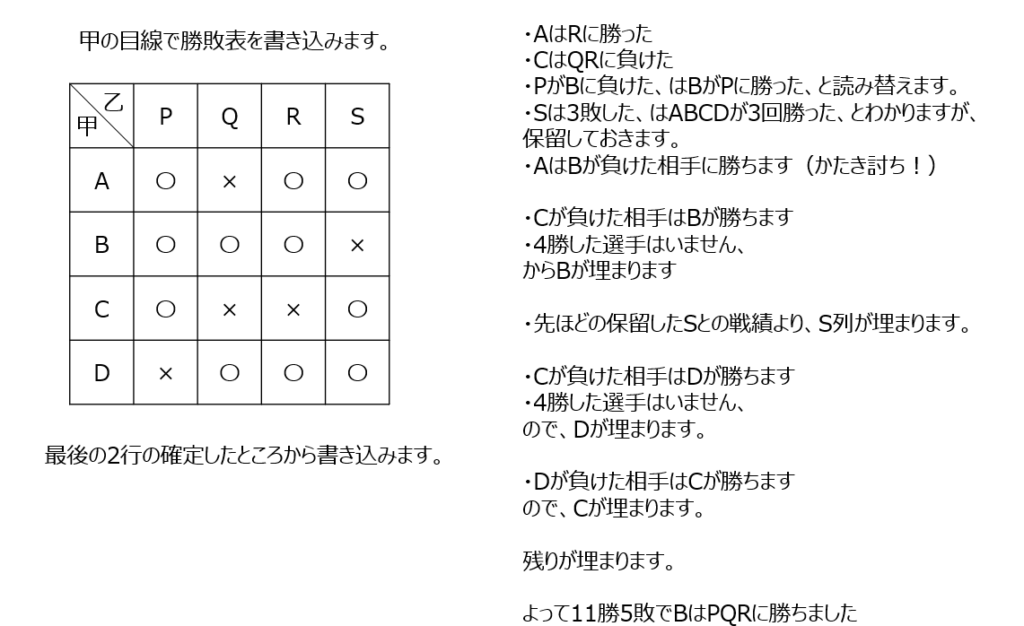
アプローチ⑦右1⃣
相手のリボンを見て自分のリボンを特定していきます、インディアンポーカーみたいですね。Bさんの気持ちになって動画では考えています。推理の要素がたっぷりの問題ですね。相手の発言から自分がわかるという、読みが必要です。動画では推理の考え方を丁寧に解説がありますので、確認してみましょう。
アプローチ⑧1⃣
サイコロを振って積と和から何が出たかを求める問題です。積や和を教えてもらってもわからない場合は、組み合わせが複数ある場合です。例えば積が4の場合、(1,4)か(2,2)か、6の場合は(1,6)か(2,3)、12の場合は(2,6)か(3,4)になります。和が4,8のだとわかるので、それ以外の5か7、になります。
まとめ
クイズ的な要素もありますが、条件から論理的思考力が試される問題なので、算数としては大切な考え方ですね。得手不得手はありそうですね。楽しく解き進んで欲しいですね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント