算数の動画「場合の数」を見ました。
苦手な生徒さんが多い部分です、といっても受ける中学によっては、まったくでない単元だったりしますので、ムキなって取り組まなくても良いかもしれません。とはいえ、実社会では確率の高い方を選ばないと損するので、大切な単元ですよね~

考え方を慣れちゃえば、何とかなる!はず!!
導入と基本②5⃣
三角形ができる点を選びます。一直線になって三角形にならない1通りを引いておきます。
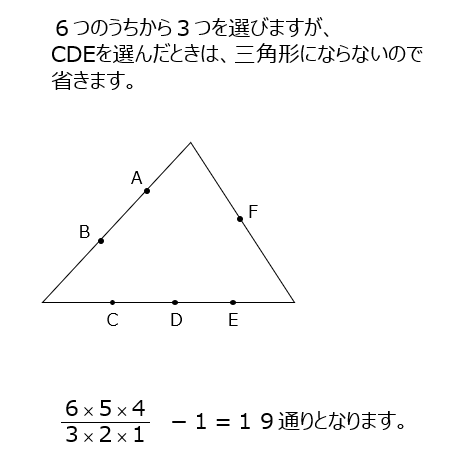
アプローチ①左1⃣
(1)100円玉と50円玉の枚数を決めれば、10円玉の枚数は自動的に決まります。
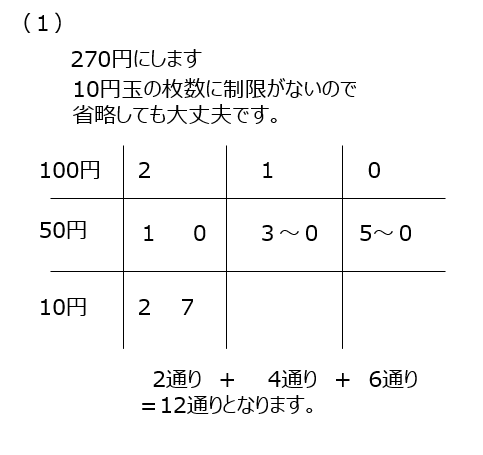
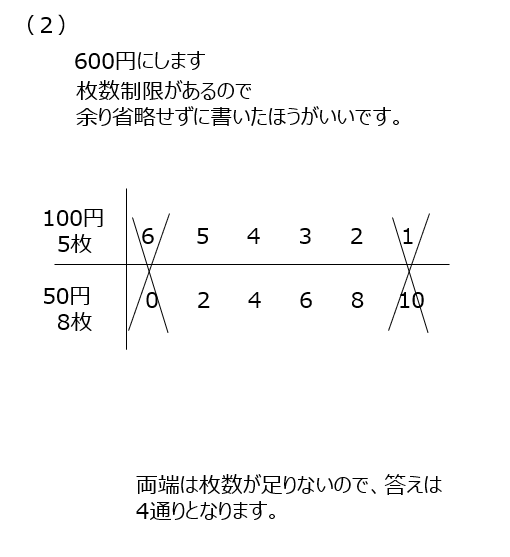
(2)枚数制限があるので、省略せずに全部書きましょう。100円玉の枚数を減らして考えて行く、などのルールを決めて書きましょう。
アプローチ①右1⃣
正三角形の一辺を、1cm、2cm、3cmとしていくと、中に含まれる正三角形の数か、1個、4個、9個と平方数で増えていきます。上向きと下向きの三角形を数えます。


補足では下向きの正三角形は上向きの正三角形に挟まれて出来るので、比べるとわかりやすいです、動画で確認しましょう。
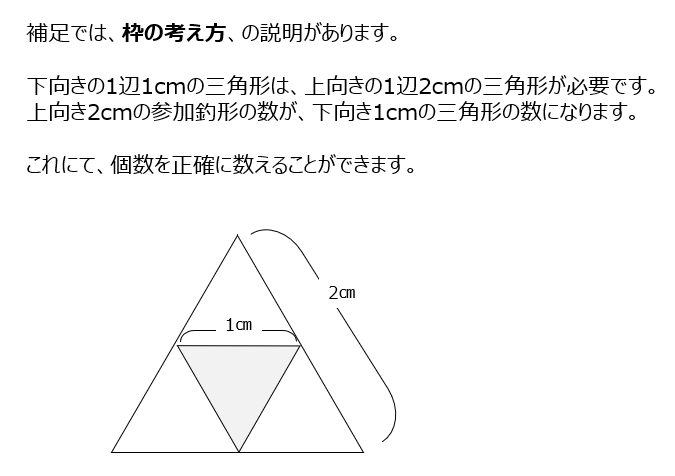
アプローチ②左1⃣
正方形の数を数えます。斜め線で作成できる正方形も忘れずに数えましょう。5種類の四角形がいくつあるか、それぞれ数えます、回転させたケースも忘れないようにしましょう。
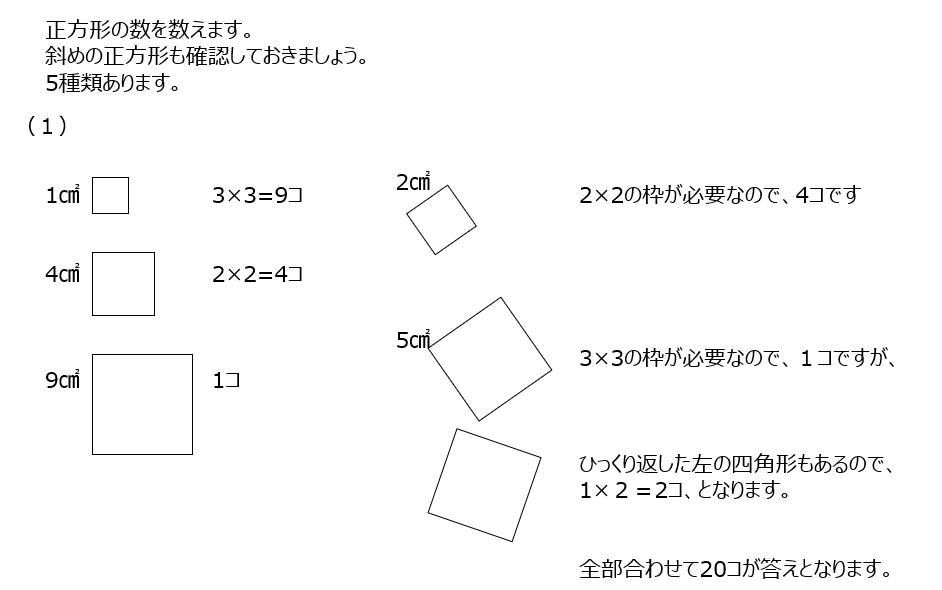
アプローチ②左2⃣
先程の問題からより数が多くなったので、丁寧に進めます。斜めの正方形の形を数値で(1,2)などで表して漏れない様に考えて進めます。動画での丁寧な説明を参照しましょう!
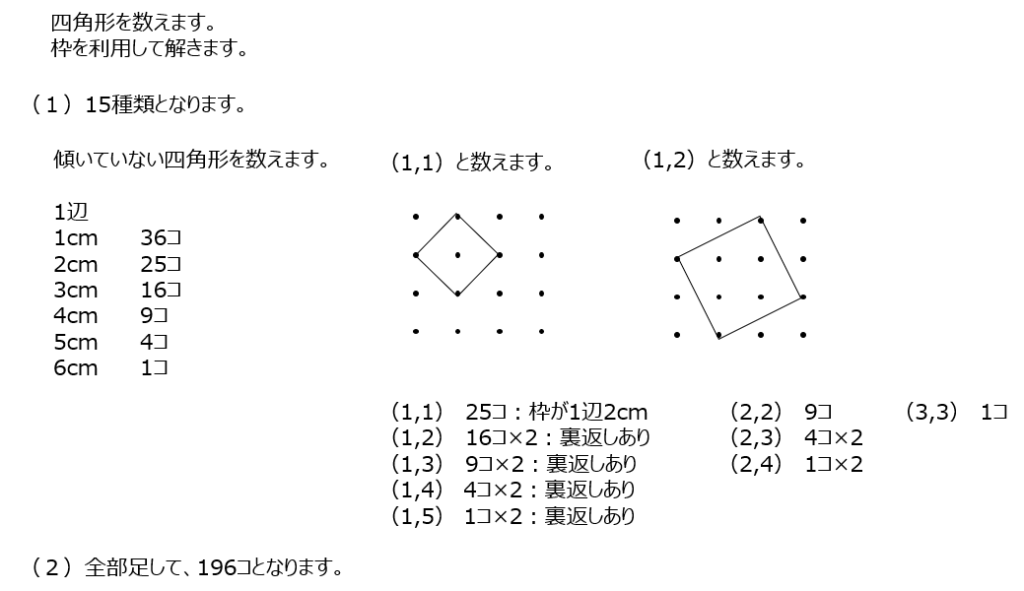
アプローチ②右1⃣
最小と最大のおうぎ形の面積比は、3.14の計算せずに出しましょう。全部のおうぎ形の数は、半径になる直線を5つの内から2つ選ぶ事になります。その中で、曲線4つの中から1つ選ぶ事になります。
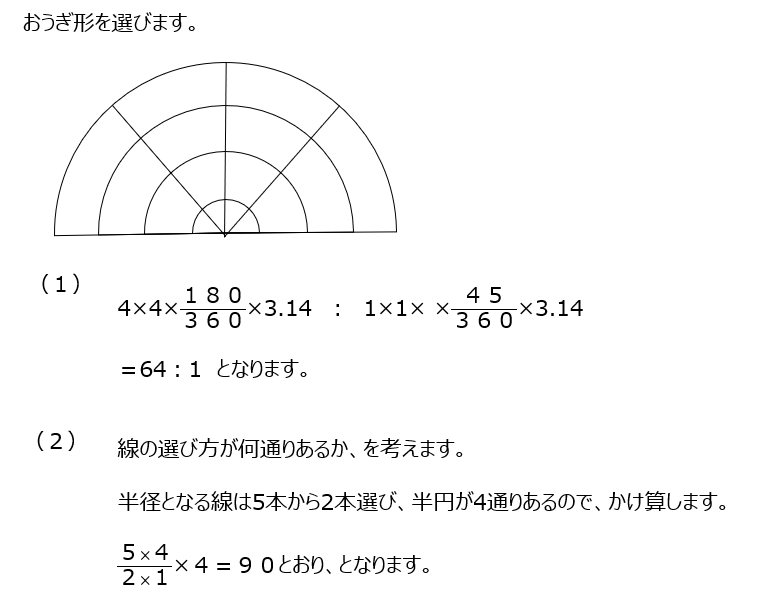
アプローチ③左1⃣
平行四辺形の数を出します。線の選び方が、何通りか、になります。
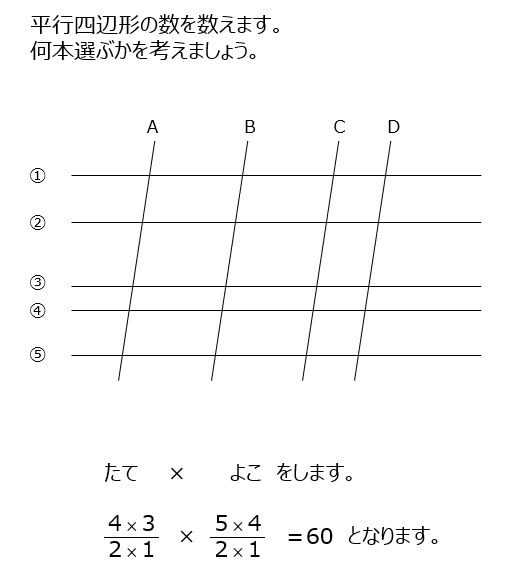
アプローチ③右1⃣
(1)正方形の数です。一辺の長さ毎に何個あるかを計算で出します。

(2)縦線と横線を選びます。聞かれてるのは長方形の数なので、注意しましょう。

アプローチ④左1⃣
三角形の数を数えます。円なので回転すると同じになることに注意して解きます。直角三角形は1本は必ず直径になる事を覚えておきましょう。動画では、何故そうなるのかを教えてくれていますので、是非確認してみましょう。直径1本あたり4つの直角三角形ができ、直径は3本です。
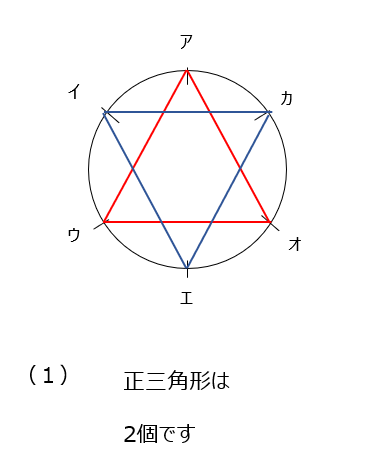
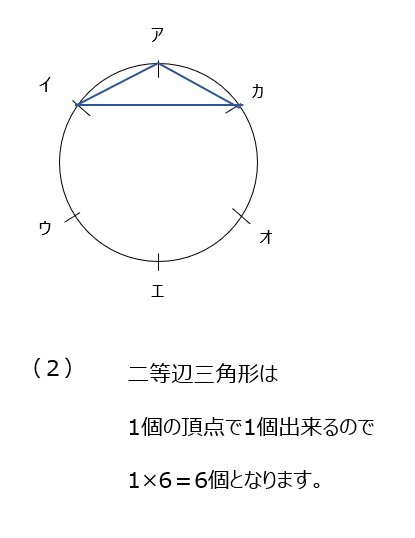
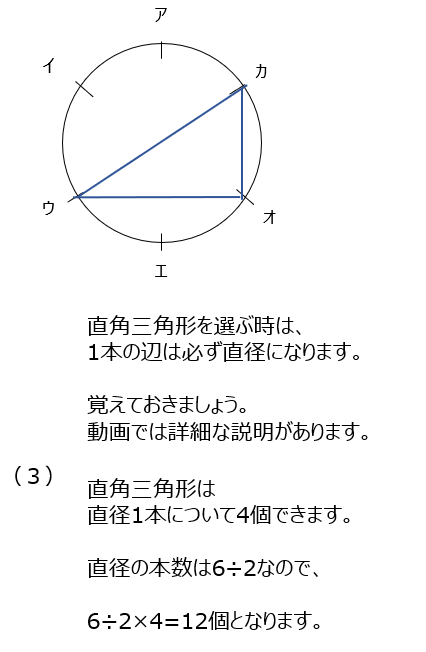
アプローチ④左2⃣
円に刻まれている点が細かくなっています。正三角形、二等辺三角形、直角三角形、を出します。解き方は前の問題と同じですね。

アプローチ④右1⃣
円周の12個の点を結んで正三角形を求めるのは今まで通りですね。長方形を求めるのは、直径を2本選ぶ事になります、覚えておきましょう!

アプローチ⑤左1⃣
動画では、答えの図からの説明になりますが、円の中の三角形で、どれが回転させたら同じか違うか、をどう考えるかの説明です。メモリを数える方法です。全4種類の図形を、和が7になる組み合わせで表しています。大事なので是非、理解して欲しいですね。
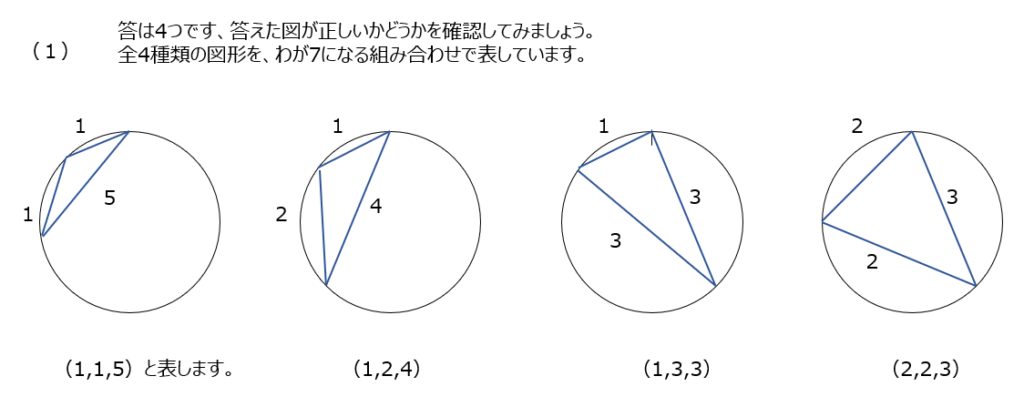
(2)では、12の和分解となります。和分解できる数を数えましょう。

アプローチ⑤右1⃣
(1)7枚で36、は数が多そうなので、逆に残りの2枚で9になる場合を考えます。次は枚数制限が無い問題です。

(2)残りが10、で考えます。

アプローチ⑥左1⃣
数の並べ方です、同じ数を隣に並べない様にします。1番数の多い2の配置を考えます。漏れない様に書き出して数えましょう。


アプローチ⑥右1⃣
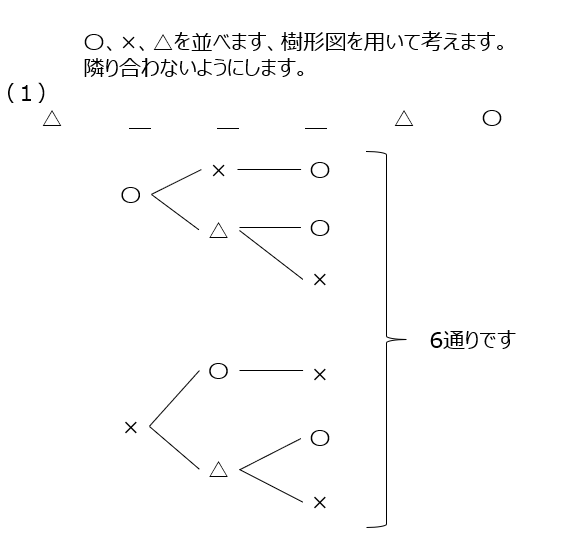
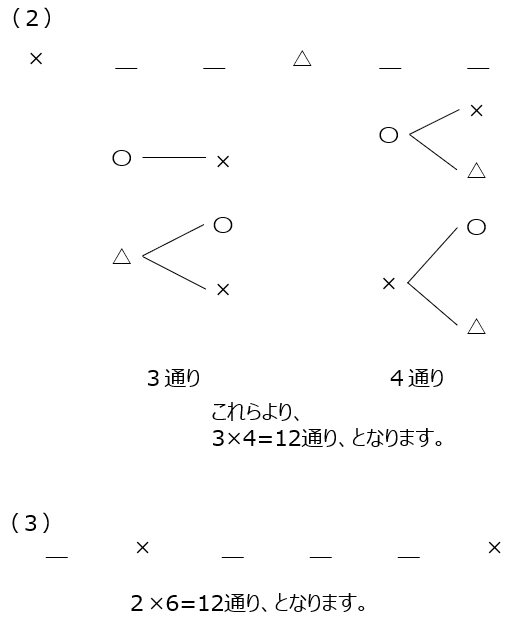
○×△の並べ方です、同じ記号が並ばない様にします。樹形図を書いてみましょう。前の小問を利用して解くと時間短縮できますね。
アプローチ⑦左1⃣
階段を何通りで登れるか、です。和分解で解きます。ある程度出すと、規則性として、二つを足すと、次が決まります。フィボナッチ数列です。
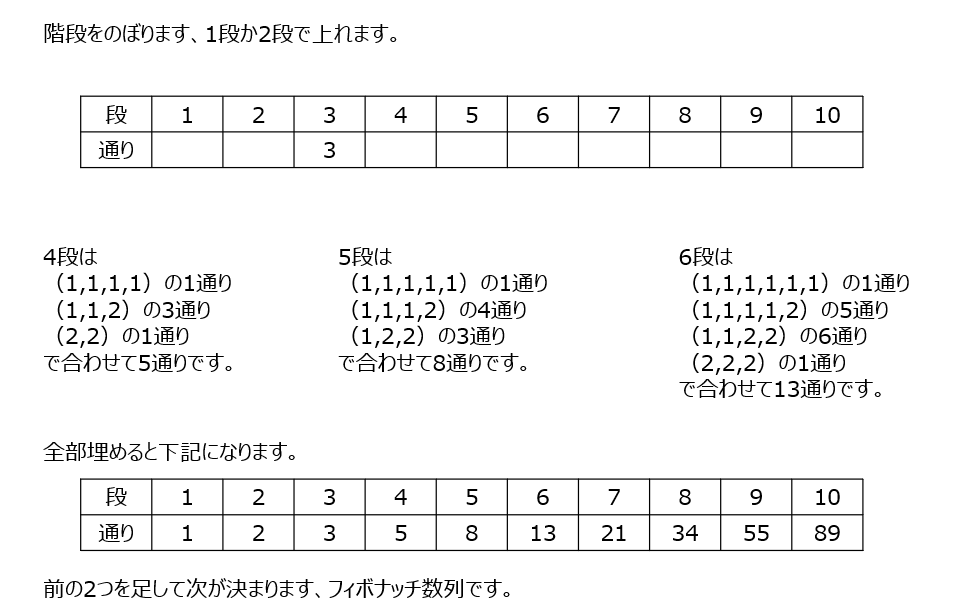
動画の補足でも説明がありますよ。
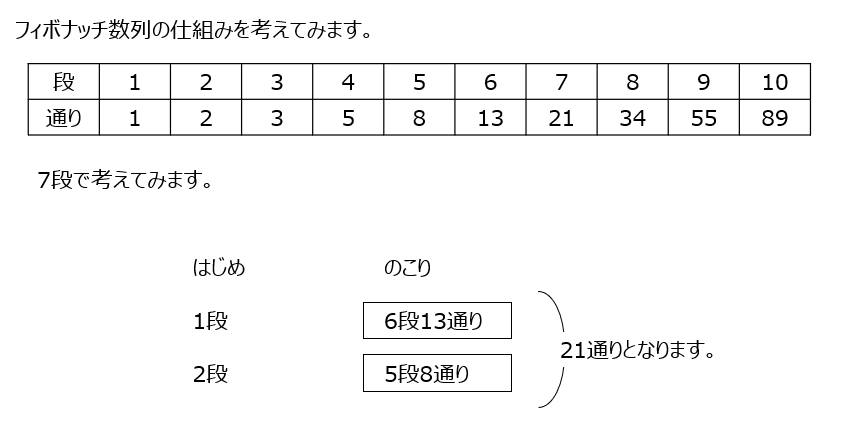
アプローチ⑦右1⃣
先程の問題と違いは3段まで登れる様になります。前の3つの数の和になっています。キチンと数えてみて、確認もしてみましょう。
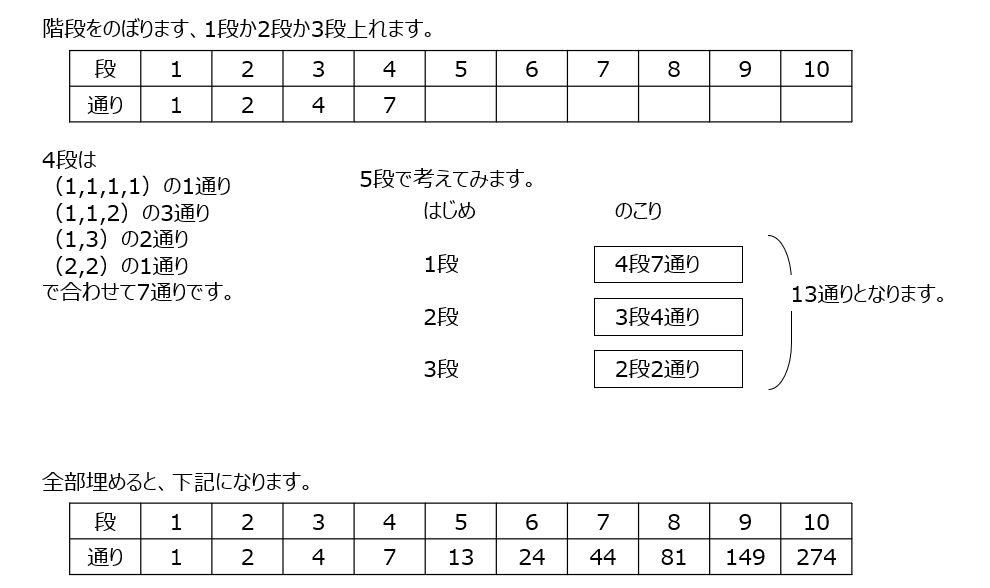
アプローチ⑧1⃣
オオカミとヒツジを入れます。初めがオオカミでも大丈夫です。まずは樹形図で考えます。別解では、3×3マスの道順で考えます。そう考えると、通ってはいけない道順がある事に気が付きます。
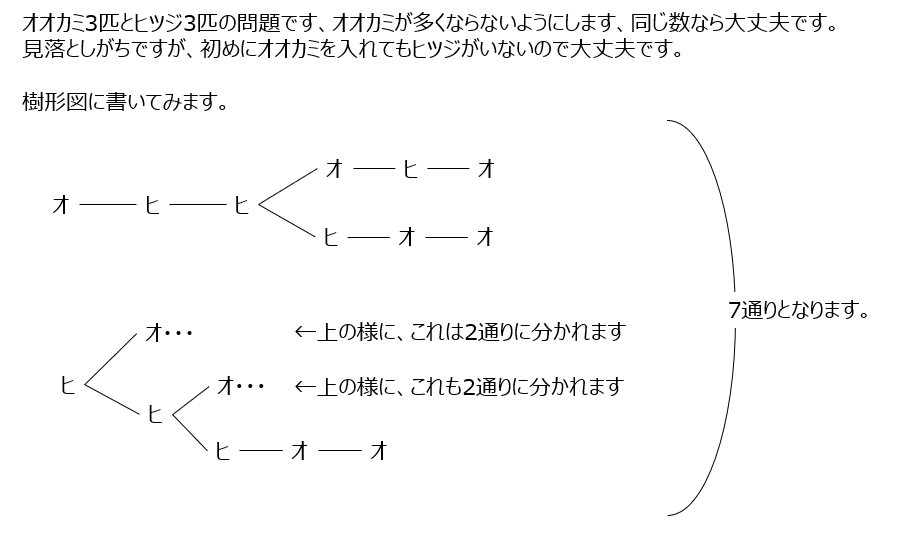
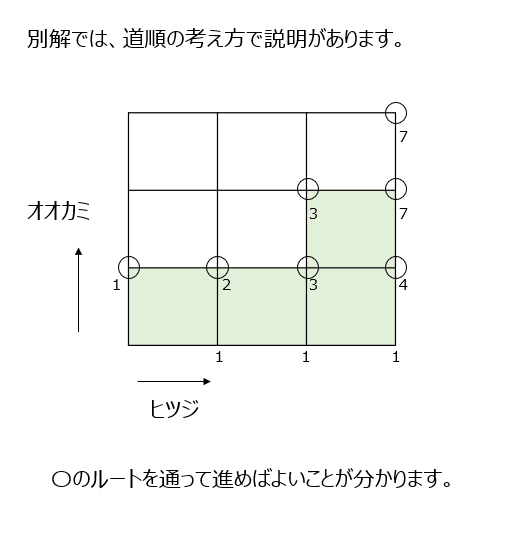
アプローチ⑧2⃣
男子と女子に先程の問題が変わっていますが、こちらも道順の解き方で考えます。通ってはいけない場所を考えて解いてみましょう。
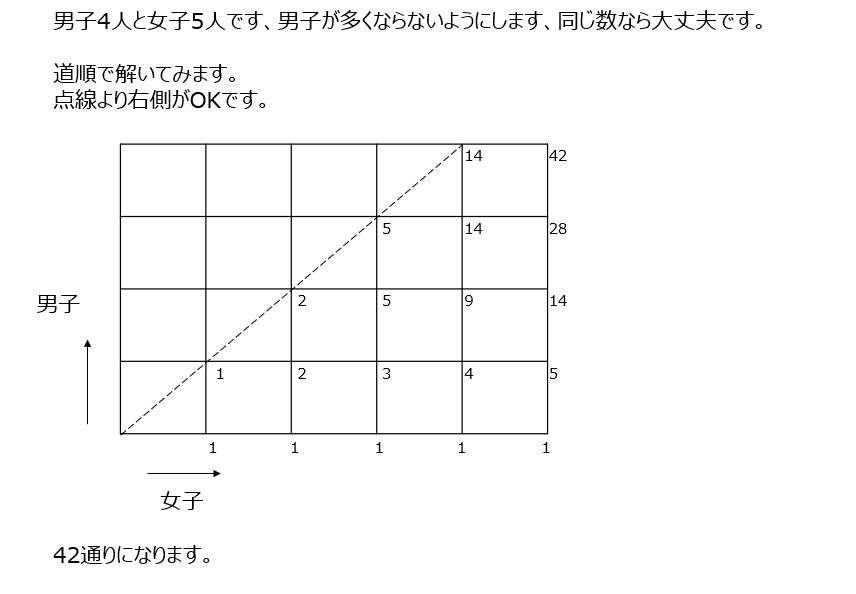
まとめ
和分解を当たり前のように使いこなせる様になりましょう!フィボナッチ数列など言葉はカッコいいですけど、規則に気づければ何とかなりそうですよ、そんなに難しく考えずに取り組んでほしいです。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント