算数の動画「表とグラフ」を見ました。
今まで習った速さの問題をダイヤグラムを用いて解きます。水槽に水を入れた深さのグラフや、図形を移動させて重なる面積のグラフ、など多数出てきます。縦軸と横軸が何を表しているか、や、グラフから三角形の相似を用いて解き進めましょう!

グラフの折れ曲がる部分に着目です!携帯会社の問題は役に立ちますね~
導入と基本①2⃣
円グラフは一昨年です。問題では昨年や一昨年を聞かれていますので、気を付けましょう。
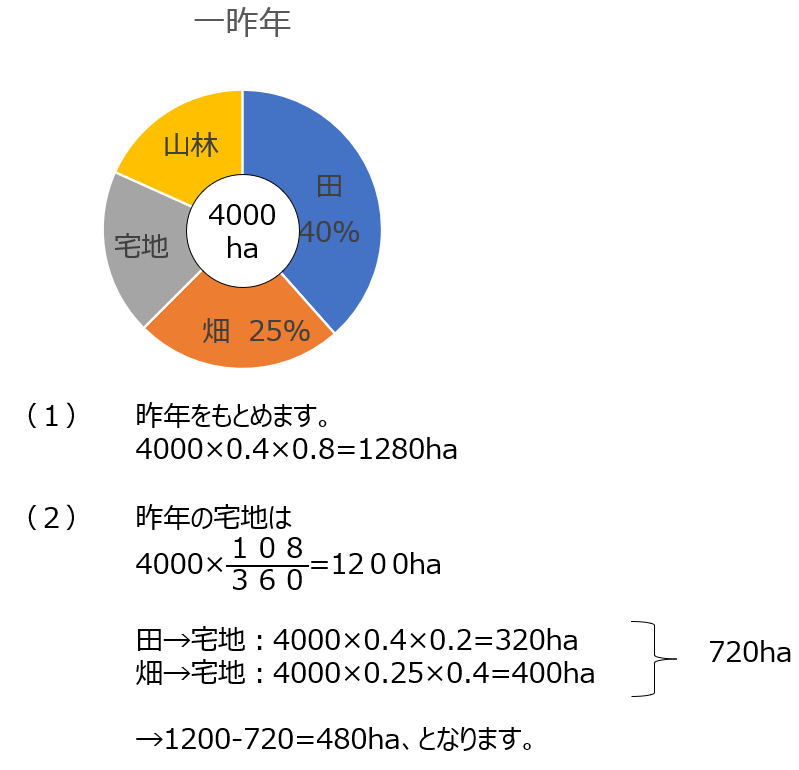
導入と基本②2⃣
水槽に水を入れます、高さがグラフで表されていますので、水の状況をきちんと確認して解きましょう。水の入る量を計算で求めていきます。各エリアの比を満杯になる時間がグラフから求まりますので、比を使って解けますよ。
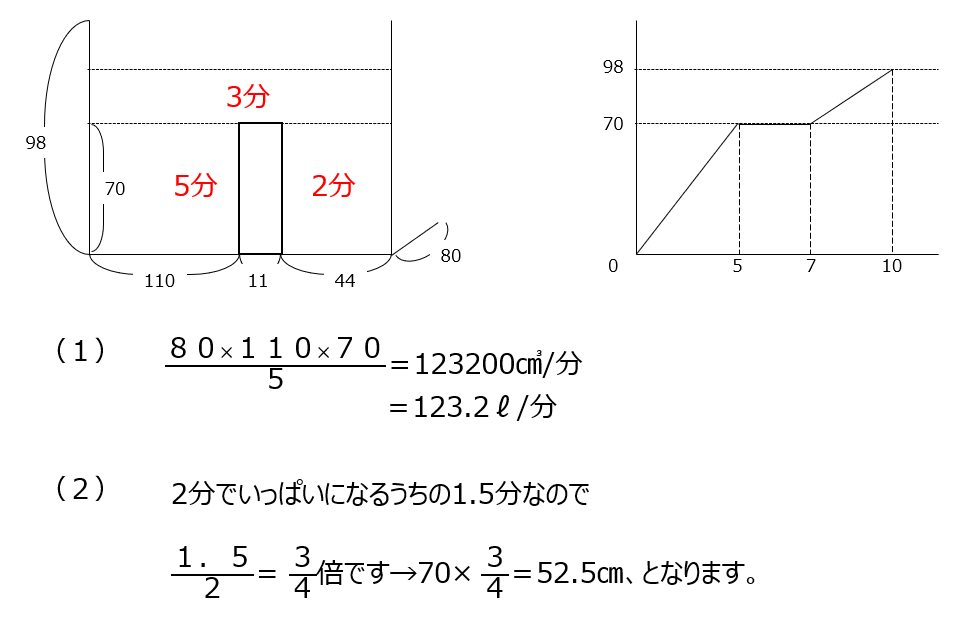
アプローチ①左2⃣
A社とB社の円グラフの問題です。最後に円グラフの角度を聞かれていますので、計算の工夫として、まず式を書いて、360°を約分せずに残して計算を進めます。
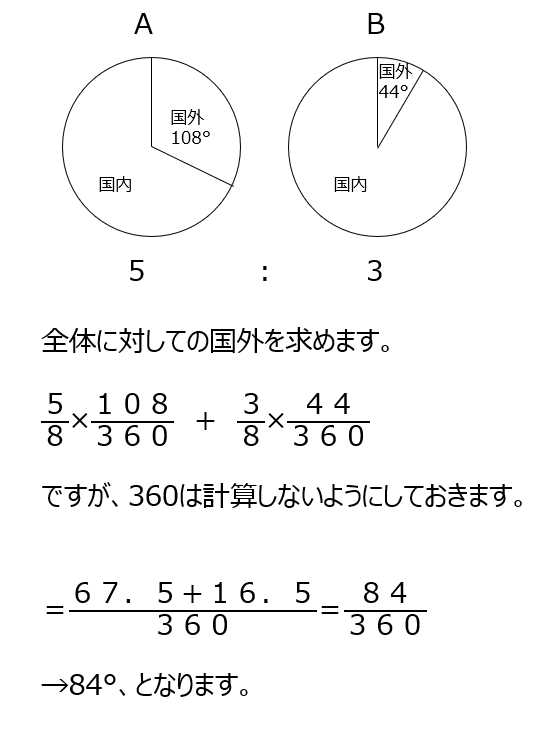
アプローチ①右1⃣
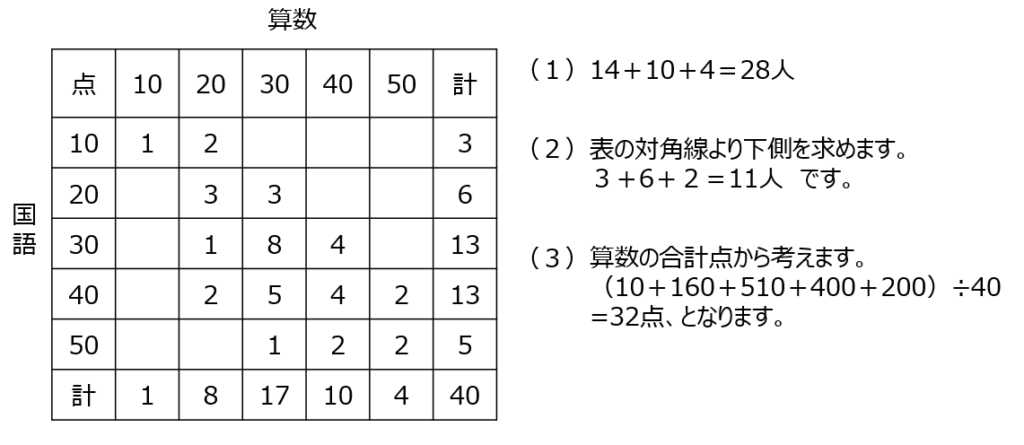
表の点数と人数から、合計を書き込んで解き進めてみましょう。わかっている部分を書き込んで求めていきましょう。アとイはつるかめ算を使いますよ。
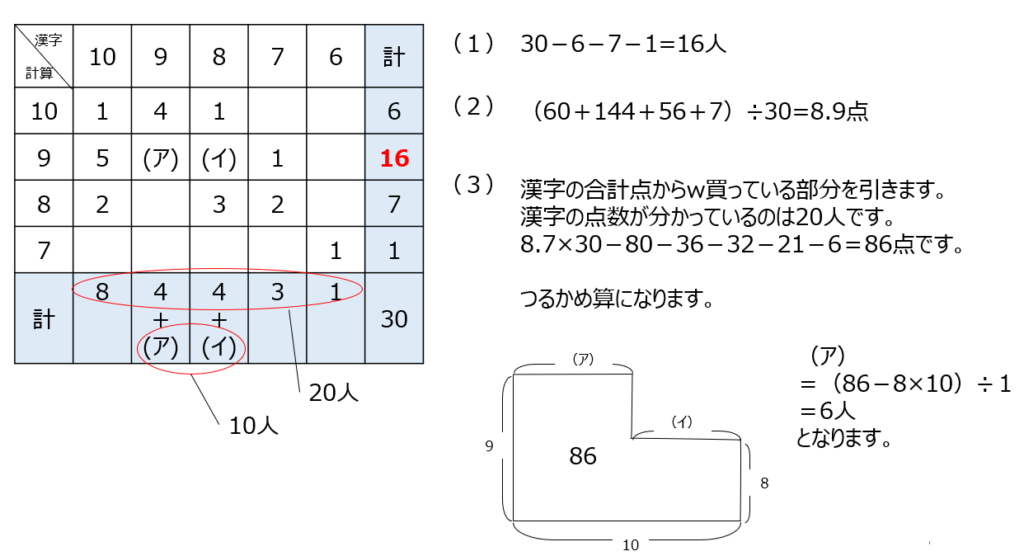
アプローチ①右2⃣
表から国語も算数も条件を満たす部分を探します。動画では、わかりやすく加工して教えてくれています。対角線より下側の人が算数より国語が高得点の人です。
アプローチ②左1⃣
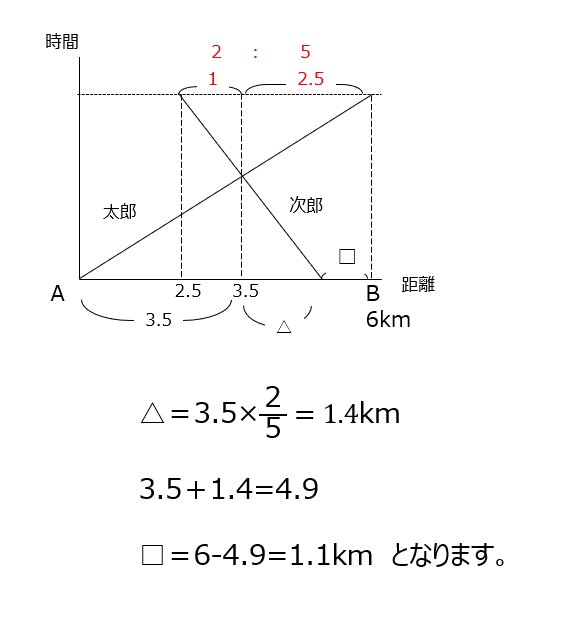
横軸が距離、縦軸が時間のグラフなので少し読み取りにくいかもしれません。太郎と次郎が同じ時間に進んだ距離がグラフからわかります。これから距離比がわかります。
アプローチ②右1⃣
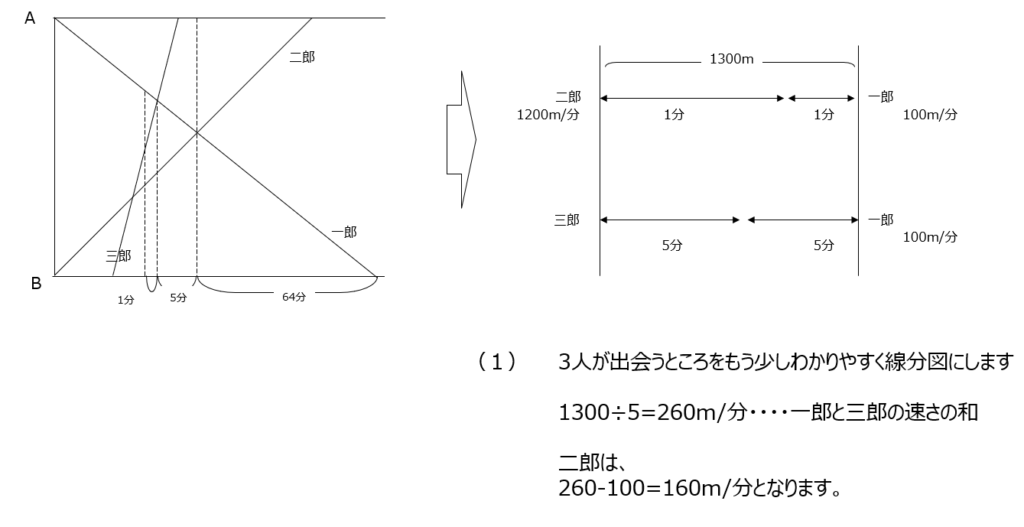
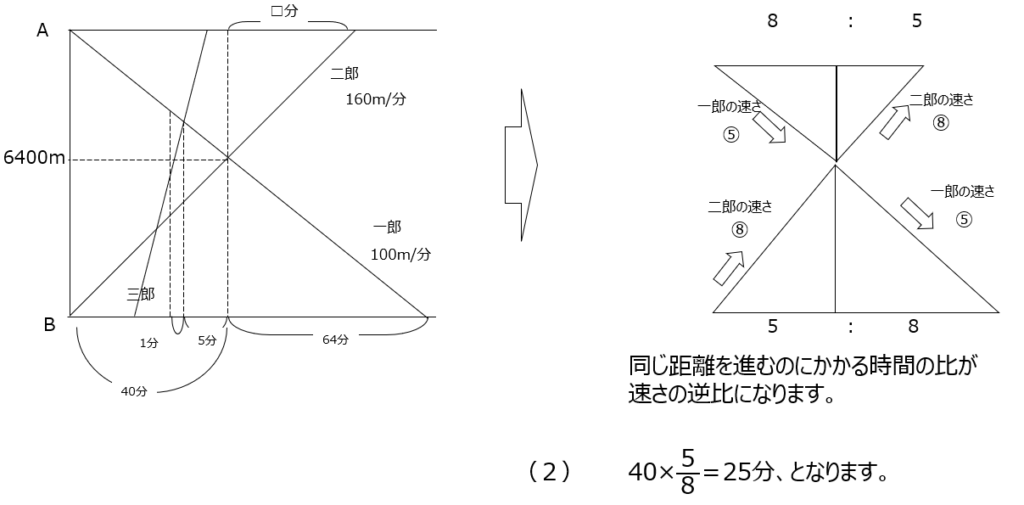
一郎、二郎、三郎の問題です。グラフが小さく見にくいので、線分図にまとめて考えています。二郎と三郎が出会った時点から、一郎とすれ違うまでで考えます。一郎と二郎の速さがわかるので、比を用いて解きます。グラフから三角形の比が使えますね。
アプローチ③左1⃣
旅人算としても解けますが、ダイヤグラムで解く方法を動画では説明有ります。ダイヤグラムから砂時計型の三角形の比を用いて解きます。
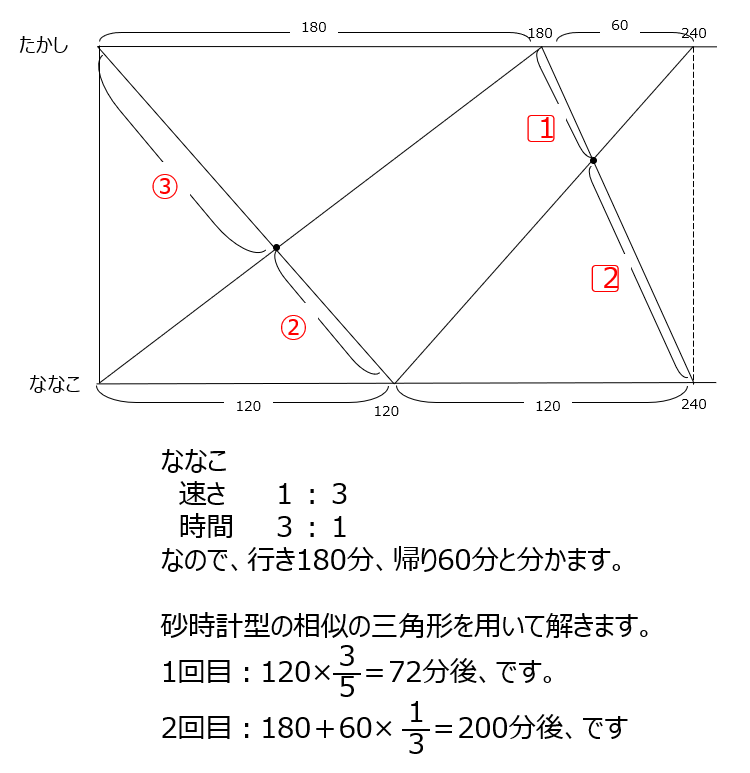
アプローチ③右2⃣
バスが往復するダイヤグラムなどです。バスと歩いている人が3回会います。極端な場合の2ケース考えます。3回目に出会うのがB地点の場合で、バスが停止したばかりの時と、停止が終わって動き出す時、の2ケースです。整数で出すように気を付けましょう。
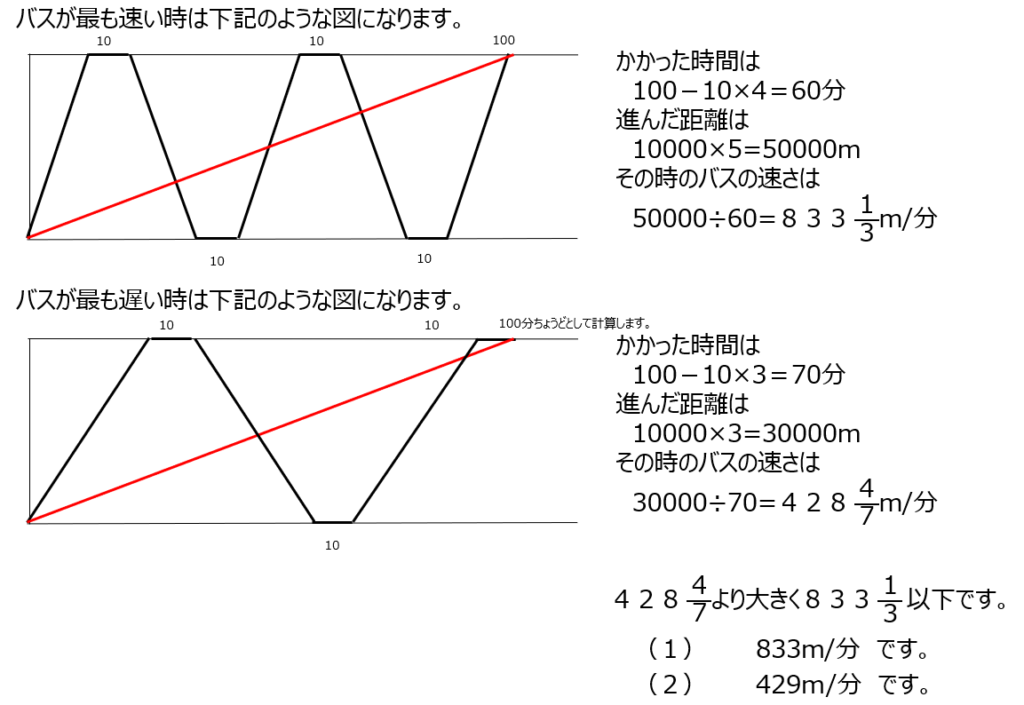
アプローチ④A1⃣
AさんとBさんのグラフを線分図で表して理解を整理します。二人の距離の差のグラフなのですが、整理して解き進めてみましょう。補足としてはグラフだけに着目して解く方法の紹介もあります。平面図形的に三角形の比を用いて解きます。
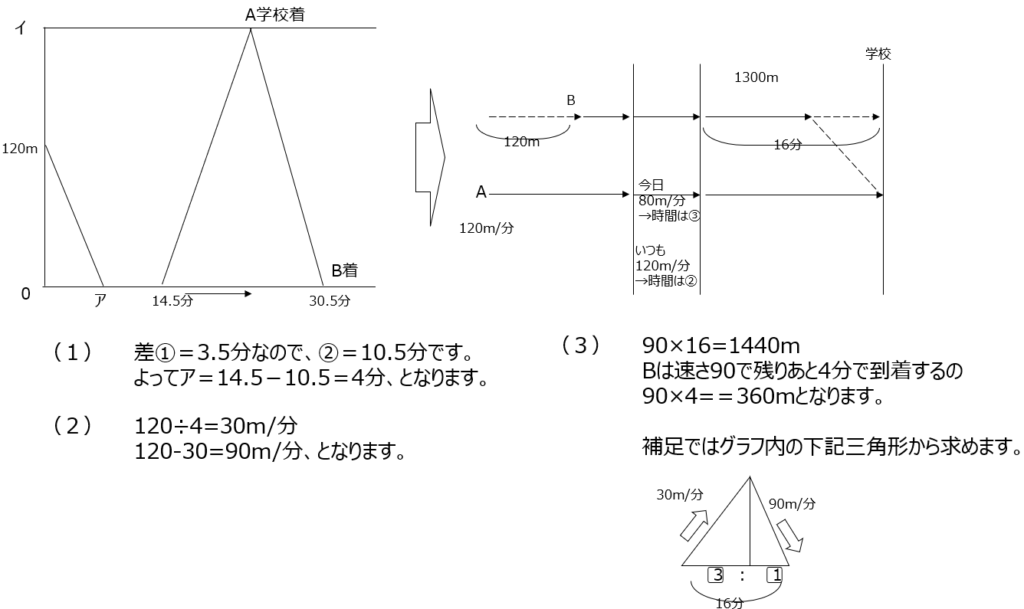
アプローチ④B1⃣
正方形が移動しますので、グラフを読み取って状況を整理して進めます。グラフの折れ曲がりが変わる時間に着目して考えましょう。グラフで面積が変わらない部分があることに注意しましょう、図形の見た目に騙されないようにします。(2)解法1で毎秒何㎠減るか、で考えます。解法2では求める時間の時の図からつるかめ算を使います。
アプローチ⑤1⃣
基本料金と通話料から、A,B,C社の料金を考えます。最初は通話料無料、などありますので、各社での通話時間などを考えますが実際にあるような問題ですね。

アプローチ⑥左1⃣
上りと下りの速さの流水算をダイヤグラムで考えます。グラフから読み取って流速を求めます。(3)の解法1では砂時計型の三角形の比で解きます。解法2では、両方の上りと下りが同じ距離を進んでいるので、速さの逆比が時間になります。

アプローチ⑥右1⃣
グラフ1,2を簡単な図にまとめて説明がります。動画はわかりやすく説明がありますね。通過算をダイヤグラムで解きます。すれ違う時と追い抜く時で、速さの和と差、がわかりますので、和差算でもあります。
実践編A3⃣
水がたまる問題です、たまった時間から比を求めます、横から見た平面で考えた時、三角形が出てきます。
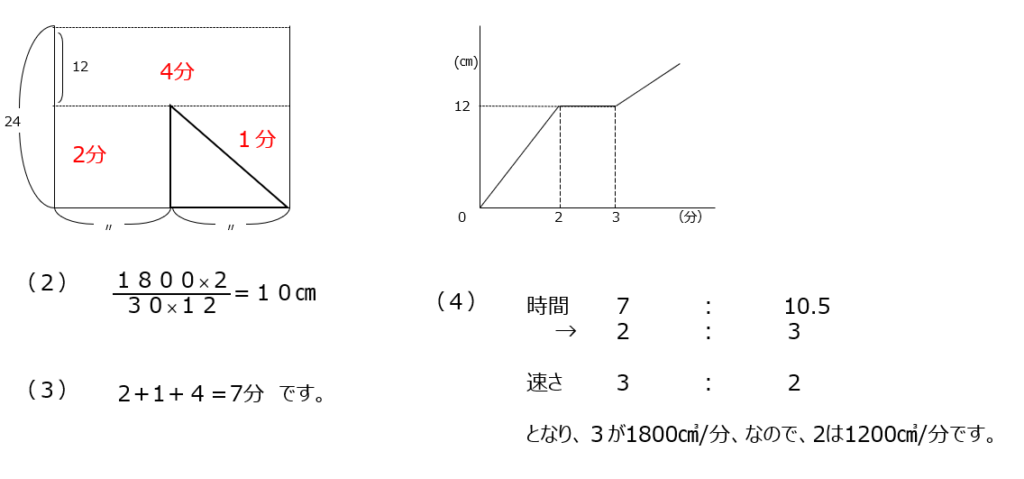
アプローチ⑧1⃣
直方体に穴をあけた立方体を切断します。横から見た平面を書いて考えます。
アプローチ⑧2⃣
直方体に穴をあけた立方体から三角すいを切り取ります。大きいほうを求めますよ。
今週の立体切断1⃣2⃣3⃣4⃣
まとめての説明があります。まずは平面で考えます。植木算的な考え方で交点の数が求まります。交点の数に1つ足して求めます。(たてー1)+(よこー1)+1なので、たて+よこー1、となります。
注意として、たてとよこの長さの最大公約数の数で考えないと、ちょうど交わる部分の重複が発生します。
立体で考えるときも先ほどの平面と同じ考え方で進めます。最大公約数があるかないか、を考えます。重複する数を引きます。4⃣ではたて、よこ、たかさ、で重複をたくさん引く必要がありますよ。なかなかむつかしいですけど、考え方に慣れましょう。
まとめ
通過算、旅人算、流水算をグラフ化しています、解くときにはつるかめ算も出てきます。他にも立体の問題では植木算の考え方も。。。。。なんでもござれ、な問題ですが、今までの知識で解けますので、粘り強く頑張りましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント