算数の動画「場合の数」を見ました。
うちの子たちは「場合の数」は苦手です、皆さんもそうなのでしょうか。説明動画はたっぷりの2時間あります、苦手意識ある方は、全部動画を見てみましょう、分からない問題だけでも見る価値は十分にありますよ。とはいえ、受験校に出ない場合もあります、過去の出題問題の確認くらいはそろそろしてもよさそうですよ。

確率論にもつながります、オトナになっても必要ですよー
導入と基本②3⃣
ゼロの入る入らないで、何通りか変わりますね。きちんと数えましょう。(1)百の位には0は入れれませんので4通り、十の位は4通り、一の位は3通り、で全てかけて48通りです。(2)一の位が0と2、で考えます。一の位が0なら、百の位は4通り、十の位は3通り、で掛けて12通りです。一の位が2の場合は、百の位は3通り、十の位も3通りなので、欠けて9通りです、併せtえ21通り、となります。(5)5の倍数は、一の位が0か5で考えます。これは(2)と同じ考え方で21通り、となります。(4)4の倍数は、下二桁が00か4の倍数です。十の位が1の時は、□12、のみです。十の位が2の時は□20、と考えていくと、□32、□52、となります。□12は2通り、□20は3通り、□32は2通り、□52も2通り、なので併せtえ9通り、となります。(3)3の倍数は各位の和が3の倍数になります。(0,1,2)(0,1,5)(1,2,3)(1,3,5)、です。(0,1,2)は2x2x1の4通り、(0,1,5)も同じ様に4通り、(1,2,3)は3x2x1=6通り、同じ様に(1,3,5)も6通りなので、併せて20通りです。(6)9の倍数は、各位の数字の和が9の倍数、になります。(1,3,5)なので、6通り、となります。
おまけ問題では、6の倍数を考えます。6の倍数は、3の倍数で且つ偶数、を探します。この問題の設定の場合、(0,1,2)では120,120,201,210なので、3通り有ります。同じ様に書き出していくと、(0,1,5)は2通り、(1,2,3)も2通り、(1,3,5)はすべて奇数なので0通りです。
アプローチ①左1⃣
(1)両端が2通りです。子供四人は、4x3x2x1で24通りです。両親は2通りです。これは父子子子子母、の24通りと、母子子子子父、の24通りなので、24×2、とかけ算します。(2)6人か2人選ぶのは6×5ですが、A君B君、とB君A君、は同じなので、2で割ります。
アプローチ①右1⃣
三角形が作れるパターンを選びます、上向きの三角形と下向きの三角形を調べます。上向きの三角形は上の線から1つを選びます、5通りあります、下の線から2つ選ぶのは3通りあります、これから5×3で15通りとなります。下向きの三角形は上の線から2つ選ぶので、5×4となりますが、2で割って10通りとなります。下の線から1つ選ぶのは3通りですので、30通りです。この2つを足して45通り、となります。
別解では、全体8個の点から3つ選びます。全体の数から、同じ線上の3つを選んだ場合を引きます。この場合、全部は8x7x6ですが、これを同じものが3x2x1あるので、これで割って全部で56通りあります。ここから、下の3つを選ぶ1通りを引き。また、上の線から3つ選ぶのは5x4x3を3x2x1で割った10通りも引くと、45通り、となります。
アプローチ②左1⃣
数の少ないみかんで考えたほうが早いです。3人にみかんを(3,0,0)(2,1,0)(1,1,1)で分けます。(3,0,0)では3通り、(2,1,0)は3x2x1で6通り、(1,1,1)は1通り、で合わせて10通りです。みかんの配り方を決めるとりんごの配り方は決まってしまうので、答えは10通り、となります。
アプローチ②右1⃣
8個のうち、3つ配るので、のこり5個で考えます。和分解では、(5,0,0)(4,1,0)(3,2,0)(3,1,1)(2,2,1)です。それぞれを考えると、(5,0,0)は3通り、(4,1,0)は3x2x1で6通り、(3,2,0)も同じく6通り、(3,1,1)は3通り、(2,2,1)も3通り、なので、併せて21通りとなります。
アプローチ③左1⃣
樹形図を書いて考えましょう。
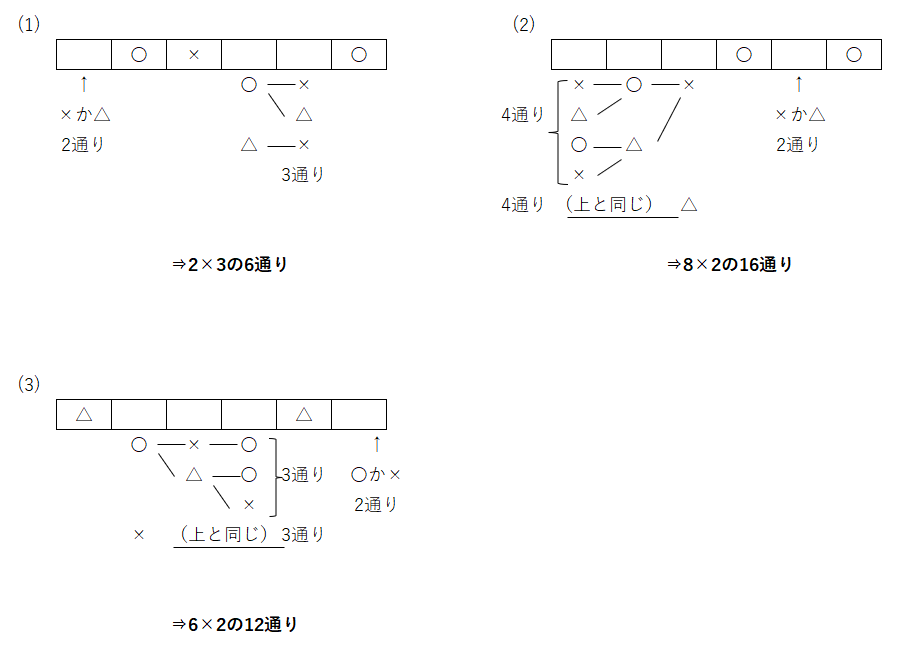
補足では、前の結果を利用する説明があります。(1)は(3)と利用します。(1)の×が無い場合は(3)と同じになります。ので、(1)で×の場合と△の場合があるのが(3)なので、(1)の答えを2倍したものが(3)の答えになっています。
アプローチ③右1⃣
塗りつぶす問題です。(1)3色から2色選ぶ場合と、3色から3色を選ぶ場合、を考えます。前者は3通り、後者は1通りです。(2)全部で3+4で7色あります、そのうち2色使っています、および、ウは赤も使えるので、1足して6通りとなります。(3)イは赤以外なので6通り、ウはイで使ったもの以外の色を塗れるので6通りです、全部で36通り、となります。(4)前の問題で、イとウで36通りあります、アは7通りあるので、全部で252通りとなります。
アプローチ④左2⃣
さいころです。出た目の和が「4」の場合の問題です。(1)全部1が出たとすると、最大4回です。(2)2回サイコロを振ったと考えると、(1,3)(2,2)です。(1,3)は2通り、(2,2)は1通りです。3回サイコロを振った場合は(1,1,2)も3通り、4回サイコロを振った場合は(1,1,1,1)の1通りで、併せて7通りとなります。
おまけ問題では、出た目の和が「6」になるとき、目の出方は全部で何通りあるか、考えてみます。和が6の場合は、2回振った時は(1,5)の2通り、(2,4)の2通り、(3,3)の1通りです。3回振った時は、(1,1,4)の3通り、(1,2,3)の6通り、(2,2,2)の1通りです。4回振った時、(1,1,1,3)の4通り、(1,1,2,2)は4×3を2×1で割った6通り、5回振ったのは(1,1,1,1,2)の5通り、6回振ったのは、(1,1,1,1,1,1)の1通りで、全部足して31通り、となります。
補足では、(1,1,2,3)と(1,1,2,2)の考え方の説明があります。しっかりと動画を見て確認してみましょう。
アプローチ④右1⃣
これもさいころを一つずつ書き出します。(1)こうたくんは17以上です。さいころを3回振るので18以下になります。(6,6,5)の3通り、と(6,6,6)の1通り、の4通りです。(2)まさしくんの合計6は、(1,1,4)は3通り、(1,2,3)は6通り、(2,2,2)は1通りで、併せて10とおりです。こうたくんは1回目が1,2回目が2でした、がまさし君が買ったので、こうたくんの3回目は1か2、となり、こうたは2通りですので、2×10の20通り、になります。(3)二人とも14になる和分解を考えます。(6,6,2)が3通り、(6,5,3)は6通り、(6,4,4)で3通り、(5,5,4)の3通り、で合わせて15通りです。これがこうたくんとまさしくん、なので、15×15で求まります。
アプローチ⑤左1⃣
(1)1位になるには、80票を何人で争う場合を考えるか、です。1位になるには2人で争うと41票が必要(過半数が必要)とわかります。(2)38票を何人で争う場合をかんがえましょうか!3位以内に入るには、4人で争う、と考えます。38÷4だと9余り2です、9票だとまだ当選確実ではありません、10票だと当選確実になります。
これは5にんを選ぶ場合は÷6をします(6人で争って負けなければ、確実に5位以内に入るれます)。同じ様に、9人を選ぶ場合は÷10をします。解き方に慣れたいですね・・・
アプローチ⑤右1⃣
当選確実となる考え方は前の問題の通りです。(1)4位以内に入るには、120を5で割ります、24票になりますが、これだと当選しないので、+1をして25票が必要となります。(2)Aが当選確実になる得票を考えます。これは動画の説明がとても分かりやすいので、動画の参照をお勧めしています。また、補足ではFはあと何票あれば当選確実か、もあります。
アプローチ⑦左1⃣
割り算してから小さい数で考えます。35xA+45xB=1260円と書きます。これを5で割って計算をラクにします、7xA+9xB=252、を求めます。A,BでBを最大にすると(0,28)です。Aは7ずつ、Bは9ずつ増やしていくと、(0,28)(9,28)(18,14)(27,7)(36,0)となります。答えは、0の時は除きます。
アプローチ⑦右1⃣
解法1では、前の問題と同じように解きます。48xA+36xB+24×C=240です、これを全部12で割って、4xA+3×B+2×C=20、で考えます。Aから決めています。Aが5だと、B,Cが0になるのでありえません。Aが4の時もありえません。ので、Aが3の時、B,Cは(2,1)となります。Aが2の時、B,Cは(2,3)となります。Aが1の時、B,Cは(2,5)(4,2)となります。
解法2ではBから決めます。Bが2の倍数、とわかるので、Bが4の時から考えてます。Bが4のとき、A,Cは(1,2)です。Bが2の時、A,Cは(1,5)(2,3)(3,1)となりますが、答え方はA,B,Cなので順番に気をつけます。
別解として、初めに1つずつ買っておく方法の説明です。
なかなか考え方が慣れるまでは難しいですが、動画ではとても丁寧な説明があるので、分からない人は動画を見てチャレンジしてみてください!
アプローチ⑧左1⃣
3段つるかめ算にまとめてみます、図にすると分かりやすいですね。
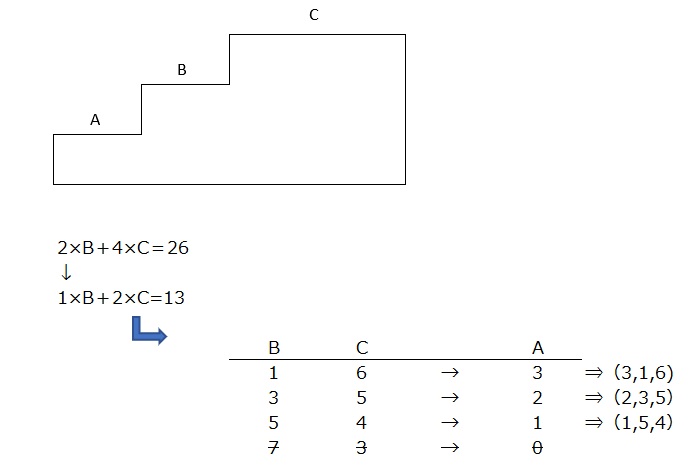
アプローチ⑧右1⃣
8回切ります。表面積を求めます。(1)もとの表面積は、(8×8-4×4)×2+8×10×4、で求まったものを3倍します、1248㎠です。(2)832㎠増えた、とわかります。切り方は3パターンあります。1回切ると2面増えます。DCで切ると4×10×2の80㎠、ABで切ると、8×10×2=160㎠、い、で切ると、48×2=96㎠増えます。これを3段つるかめ算をしても良いのですが、今回は式で解きます。
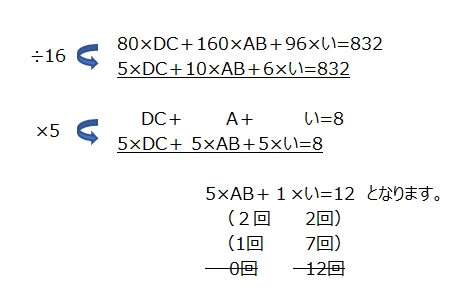
動画で確認してみましょう。
実戦編C1⃣
樹形図を書いて見てましょう。Aが座っていた椅子にBが座ると、して考えていきます。全部で9通りあることが分かります。
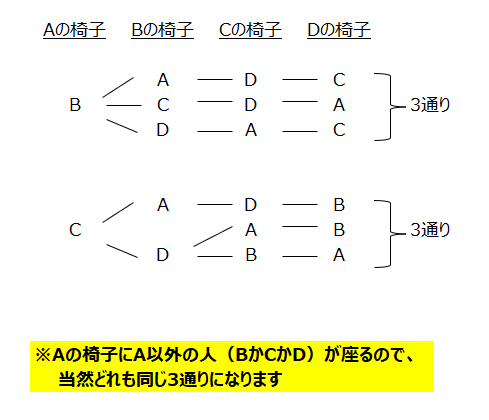
実戦編E1⃣
塗分ける問題です。いままでのやり方の塗分けの考え方では出来ない問題です。(1)同じ色で問題ない場所はADとBCです、4×3の12通りとなります。(2)ADとBとCで考えます。4×3×2の24通りとなりますが、BCが同じ色でAとDに分かれた場合も同じく4x3x2の24通りあるので、併せて48通りです。(3)4色つかうのは、4×3×2×1の24通りです。これらより、今までをまとめて、12+48+24=84通り、とわかります。
難易度高いですね・・・動画で確認しておきましょう!
今週の立体切断1⃣
求める体積は引き算で求めます。相似の三角形を使います。動画での図を用いた解説がわかりやすいですので確認をお勧めします。
まとめ
場合の数は大人も苦手意識あるので、子供も得手不得手がはっきるする単元です。きちんと動画で理解しておきましょう。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント