算数の動画「規則性に関する問題」を見ました。
植木算や方陣算、といった懐かしの単元もありますが、6年生になって総合的に考えます。解法も複数用意されていたりするので、幅を広げる意味でも、聞いておくくらいはしておきたいですね。

さぁ、始めましょう!
導入と基本①1⃣
植木算ですが、引っ掛け問題ですね、よく、問題を読みましょう。300÷3=100は間の数です。これに1本足して101本ですが、これは答じゃないです。道路の両側ですので、×2をして202本、となります。
導入と基本①3⃣
のりしろの考え方ですね、2つの解法を理解しましょう。解法1では、30cmに29cmずつ伸びていく、という考え方です。15枚繋ぐので、29は14回加わりますので、30+29×14=436となります。解法2では、全体30cmが15枚から、のりしろ分1cm×14を引く方法です。
導入と基本③4⃣
規則性に気付いて、グループに分けて考えます。「2,3,1,2,4,2」が繰り返されます、これを1グループとして考えます。(1)99÷6で、16グループあまり3となります、17グループの前から3つ目は1,となります。(3)グループごとに足します。1グループの和が14なので、14×16グループ+2+3+1で230となります。(2)2が99個、なので、1グループあたり2は3個あるので、99÷3=33グループまでが必要、とわかります。何個目か、は最後の2はグループの最後の数なので、ちょうど33グループ、と考えて、6×33=198番目、となります。
アプローチ①左1⃣
リングの内側の円、で考えます。リングの内側は10cmです、次のリングも内側が10cm、、、、と続きます。最初と最後の幅1cm(併せて2cm)を忘れないようにしましょう。(1)40個あるので、10×40+2=402、となります。
(2)数だけを出してみると、「1,10,10,・・・・・、10,1」となり、これら全部の和が672となるので、(672-2)÷10=67個、と求まります。
アプローチ①右1⃣
赤、青、黄色の輪の色の違いを考えます。すべて縦向きで考えます。最後割り切れない考え方、しっかりおさえましょう。(1)先ほどと同じ様に、2+2+10×3=34、となります。(2)先ほどと同じ様に、(194-4)÷10=19個、となります。赤、青、黄を1つのグループで考えます。19個÷3=6余り1なので、このあまりは赤色を差しています。(3)黄色が13個で、最も多い個数を求めます。グループを作ります。グループは13個必要ですが、最も多い個数を求めるので、14グループ目の赤と青、までつなげたのが最も多くなります、これに最後の2cmを足します。2×2+30×13+10×2=414cm、となります。
アプローチ②左1⃣
縦切りか横切りかです。(1)縦切りにすると、テープを16本も切ります、のりしろ2cmは15個です。全体では40cm×16-2cm×15で610cmです。(2)横切りにすると、テープは8本です、のりしろは7個です、80×8わー2×7=626cm、とわかります、差は16cmとなります。
補足では、のりしりの数だけで考えます、40×16と80×8は同じなので、のりしろだけの差で良くなります。
アプローチ②右1⃣
20,10,20,10、、、と切っていきますので、20,10を1つのグループとしてみます。300÷(20+10)で10グループあります。ので、全部で20個の木がある、とわかります。切った回数は19回、となります。休んだのは18回となります。8分×19回+2分×18回=188分、となります。最後は休憩しないですよ。
アプローチ③左1⃣
図に書くと分かりやすいですね、外側がいくつか、間違えないようにしましょう。
(1)縦横1列ずつ並べられたとして、それに必要なおはじきの個数を考えます。差の33枚は追加した赤い部分になります。(33-1)÷2=16から1辺が16とわかります。これから最初の枚数は16×16+24=280枚となります。
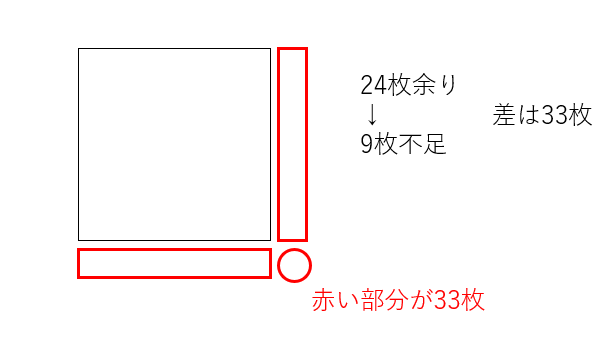
(2)赤い部分の長さは(20-4)÷2で8とわかります。元の長さは縦11、横8,とわかるので、8×11+15の93、とわかります。

アプローチ③右2⃣
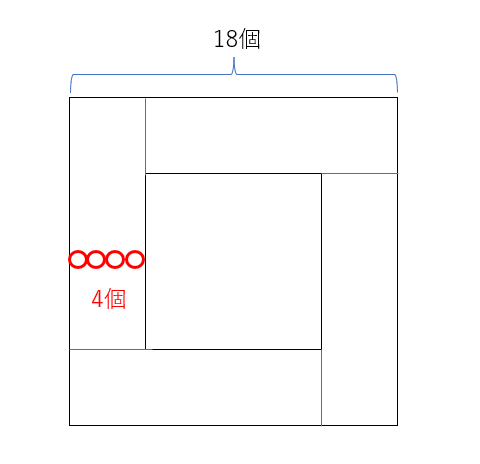
中空方陣です。下記のイメージです。解法1では周りを4つに区切って考えます。1つの区切りは14×4=56個なので、56×4=224個、となります。解法2では、真ん中に穴が空いていない考え方です。全体18×18-10×10を引いて求めることもできます。
アプローチ④左1⃣
何重かになりますが、考え方は同じです。図を書きながら考えましょう。
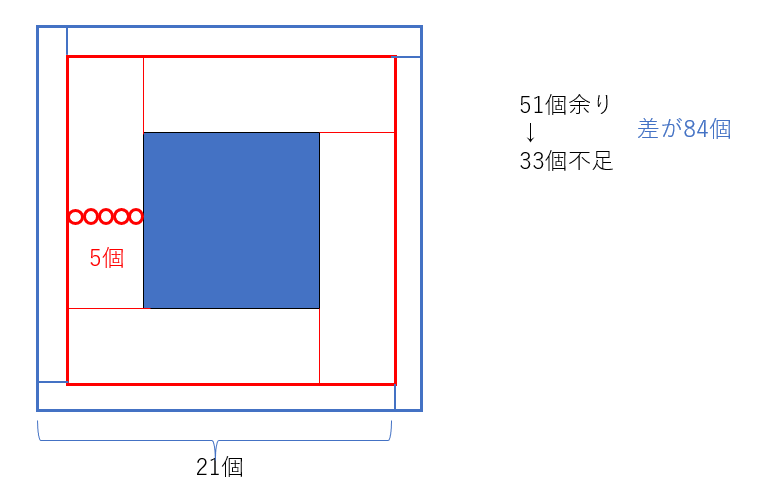
1まわり並べられたとして、それに必要なおはじきの個数を考えます。差は84個となります、外側の青色の部分の個数です。下記から長さ分かりますので、書き加えて考えましょう。赤は5×15×4で300個、青は10×10+51で151個ですので、差を求めることができます。
アプローチ④右1⃣
長方形を書いて考えます。37人余って、1列追加すると、10人不足します。差の47人は追加した部分です。縦と横の合計が46人とわかります。縦と横の関係を式に書きます。縦×4=横×5+13、と縦+横=46の2つの式で消去算をして求めます。
アプローチ⑤左1⃣
表面積を求めます、表面積が問われているので、立体の下の面も含みます。自分で表を書いてみると分かりやすくなります。(1)3段だと、1+2+3=6㎠が、前後左右上下の6方向で見えるので、6×6=36㎠とわかります。5段だと、1+2+3+4+5=15㎠が6つ見えるので、15×6、で求まります。(2)6段までを足します、三角数です、56個、と求まります。(3)見えないイメージを動画では説明があります、確認しておきましょう。9段までなので、56個、と求まります
| 段 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 個数 | 1 | 3 | 6 | 10 | 15 | 21 | |||
| 見えない個数 | – | – | – | 1 | 3 | 6 | 10 | 15 | 21 |
アプローチ⑤右1⃣
分子と分母の和が一定なことに気付きましたか?(1)分母と分子の和が261なので、分子を求めれば分母が分かります。答えは約分せずにそのままの形で答えましょう。(2)130分の131、となるので、分子が131となるのは(131-1)÷2+1で66番目、とわかります。(3)3で約分できるものは、分子が3の倍数であればよいので、分子だけで考えます。分子は、3,9,15,21と6ずつ増えていきます。1より小さいので、分子が129まで、となります。(129-3)÷6+1=22個、と求まります。
(2)のおまけ問題では、初めて1.5より大きくなる分数を求めます。まずは、分子と分母の比が3:2とすることから考えます。104.4分の156.6なので、この次の104分の157、が答えとなりますが、157が分子になるかどうかは確認しておきます。
アプローチ⑥A1⃣
ひっくり返す考え方は、初見は難しいですが、分かると理解しやすいですね。動画での詳しい説明を確認してみましょう!(1)20段目は1+2+3+、、、と20まで足します。(2)4段目、5段目、11段目、12段目までをそれぞれ出して、足し合わせます。(3)同じ問題を2問連続で出すのは、なぜか、に気づけましたか?工夫して求めることができます。動画では図形と式の両方で説明が丁寧にあります、とても分かりやすいので是非とも確認しておきましょう。
アプローチ⑦1⃣
三角に並べていきます。(1)下記の図のイメージです。全部で等差数列の考え方から(1+9)×9÷2で45個、と求まります。
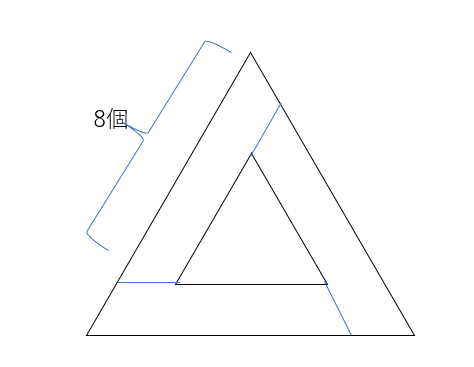
(2)3段分追加すると下記になります。上の段+(上の段+1)+(上の段+2)が45個なので、上の段が14、とわかります。これから、(1+13)×13÷2,で求まります。
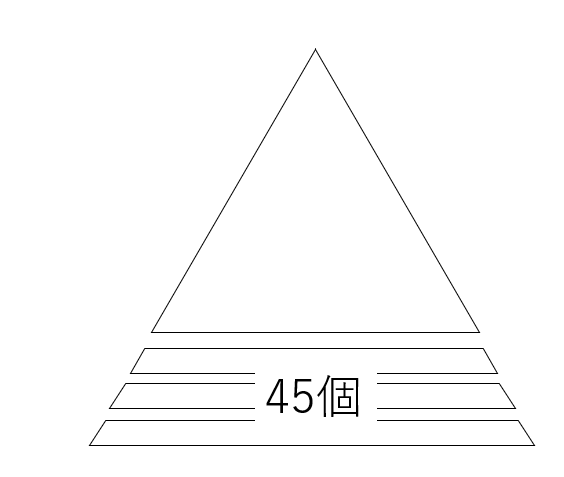
(3)解法1では、まずは1個の三角形を囲んでいく考え方を確認します。はじめの1だけ例外ですが、1,9,18,27,36と9ずつ増えていくことが分かります。3個の3角形を囲んでいくと、3,12,21,30、とこれも9個ずつ増えていきます。動画では線分図で整理して説明があります。解法2では中空方陣を使って考えます。追加されていく個数は真ん中が平均になります。解法3では先ほどの(2)の考え方を使って解く方法の説明があります。
アプローチ⑧B1⃣
奇数、偶数で差の違いを考えます。グループにまとめて考えます。動画での説明がとても分かりやすいので、解説見ても分からない方は動画を確認してみましょう。(1)グループ番号と差の値を合わせると30で一定であることから、考えると簡単です、30グループになります。(2)グループ番号が23-1=22増えるので、30も同じだけ増えます。(3)偶数番目の数はグループでまとめないほうが考えやすいです。(4)70グループになります。
実戦編B1⃣
まずは問題を確認します。曲線部分は、直線部分に居る人を除いた状態で考えています。曲がっている部分には24÷3+1-2、で7人います。直線部分は30÷3+1で11人います。合わせて7×2+11で25人、となります。別解では池の周りの考え方で説明があります。
実戦編B4⃣
今までの考えかたを使いましょう。(1)1/4、2/8、、、と並べていき25/100となるので、全部で25個あります。(2)同じ様に、1/6、2/12、、、、としていくと16/96となり、16個となります。(3)分母でグループ分けします、全部に大きさ1になるものがあるので、100グループあるので、100ある、とわかります。(4)4分の1、4分の2,4分の3,4分の4、とそれぞれ考えていきます。動画での説明がとても分かりやすいですね。
今週の立体切断1⃣
立方体の切断面を考えます、考え方としては、中途半端なところで止まっているので、もっと大きな図として、横に広げて考えます。広げていくと、砂時計の相似の三角形が見えてきます。どこで交わっているか、は図を丁寧に書いていくと間違えないのですが、微妙な場合は、途中で相似の三角形の長さを出しながら、おかしな数字にならないことを確認しながら解き進めましょう。大きな三角すいから、小さな三角すいを2つ引く、という考え方で求めます。動画での図を見ながら解き進めてみましょう!最後に2⃣についてのコメントがあります、解き方はこの問題の動画と、解説では違う方法なのですが、どちらも大切な考え方なので、余裕のある人は是非とも確認してみましょう!
まとめ
テクニカルな部分もありますが、基本を理解しておかないと解けない問題が多数あります。たくさん問題を解いて、経験を増やしましょう!苦手なところはやり直しておきましょう、苦手な部分だけでも、動画を見て確認しておくのもよいかもしれません。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント