算数の動画「数の性質(2)」を見ました。
夏期講習初日にした数の性質です、2週目に入りました!難易度は少し上がっているかもですが、(1)で習ったことが出来るようになっているかの確認にもなりますね。ここで分からないものが無いように復習しましょう。

公倍数、公約数、素因数分解、ベン図と使いこなしましょう!
導入と基本①4⃣
(1)掛け算して整数にします、分母の倍数になりますね。3と4と9の最小公倍数を求めます。でも、4と9の最小公倍数でオッケーですよね。(2)求める分母は、最大公約数です。

導入と基本②2⃣
3つ同時に考えるのは難しいけど、、、、全部書き出す必要はありません。(1)24の倍数+3と、9の倍数−3で考えます。(2)999以下を探します。(3)等差数列の計算です。
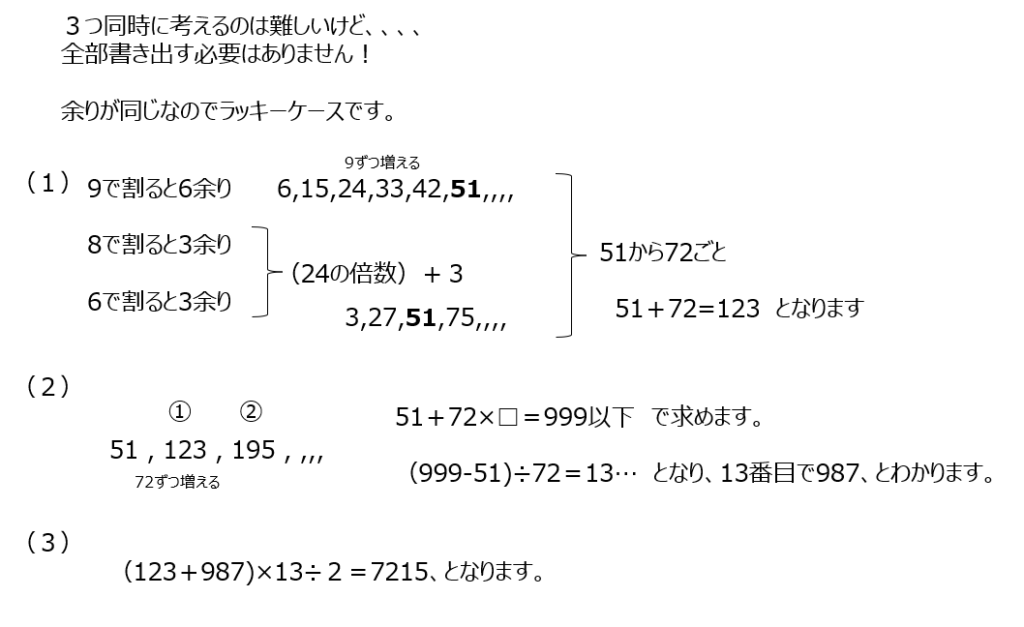
導入と基本②3⃣
長方形を繋げて正方形を作る問題です。最小の正方形は6枚で作れて、1辺が30cmです。これが、30の倍数で大きくなっていきます、そして枚数を計算します。動画の説明は図示していて、とてもわかりやすいです。
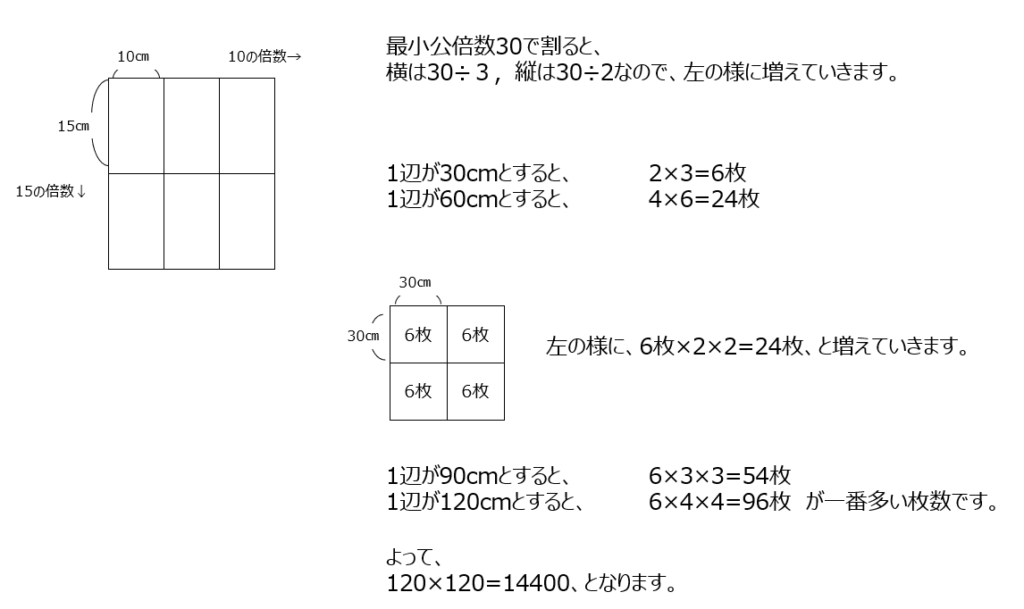
導入と基本②4⃣
比率で考えます。この問題は数値が簡単ですが、動画ではそうでない場合についても言及しています。
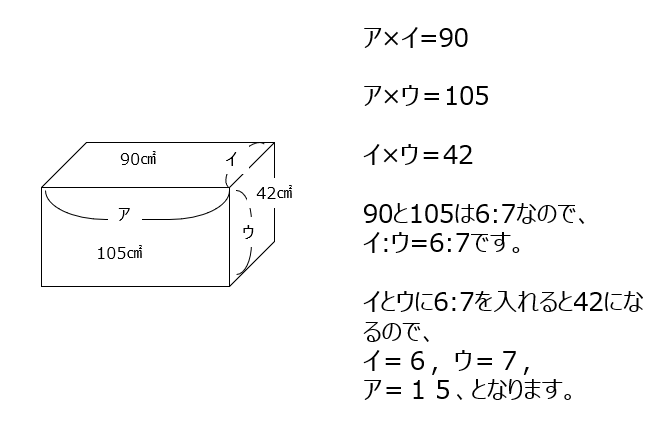
導入と基本③1⃣
素因数分解します、分母に付け加えてかける数がAになります。
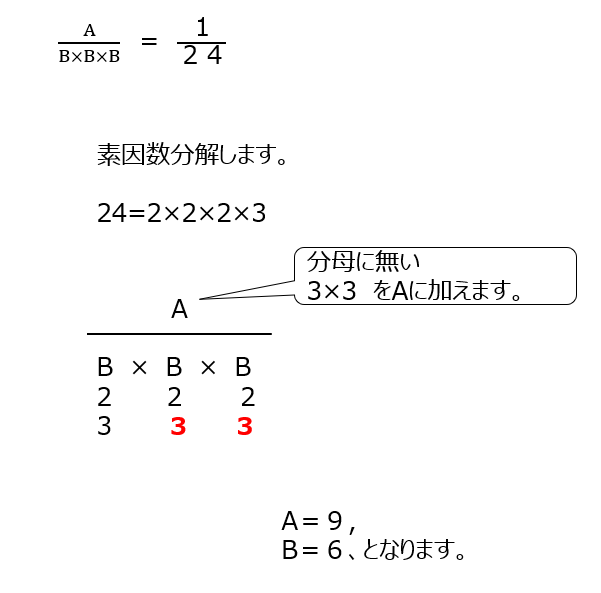
アプローチ①左1⃣
(1)xとyまでは出せますが、この2つの数は、もう割れない関係になっていますので、そこを気をつけましょう。(2)26で割り切れる、は、分数て約分して分母が消える、という考え方です。
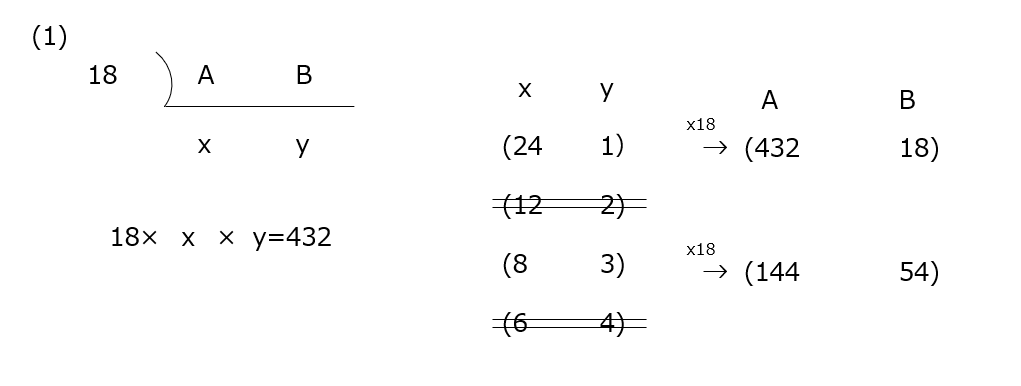

アプローチ①左2⃣(2)
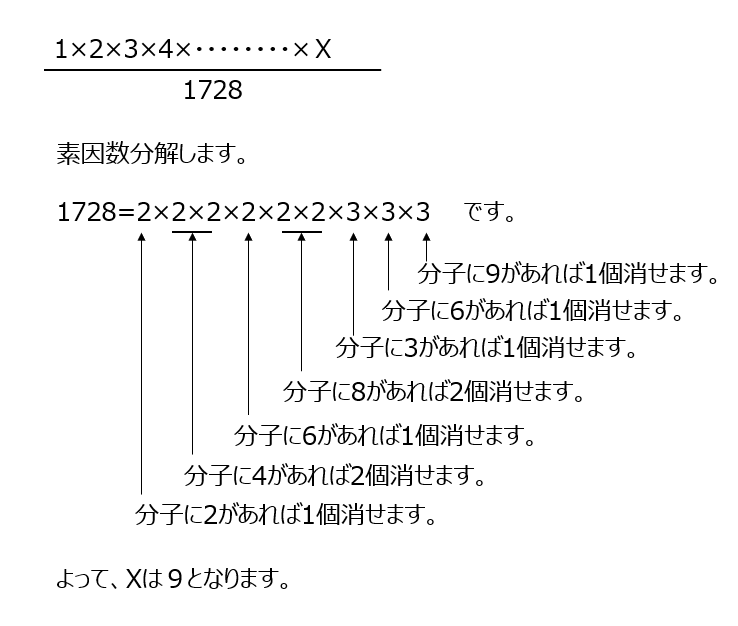
1728、がどう割り切れるのか、考えます、素因数分解です。
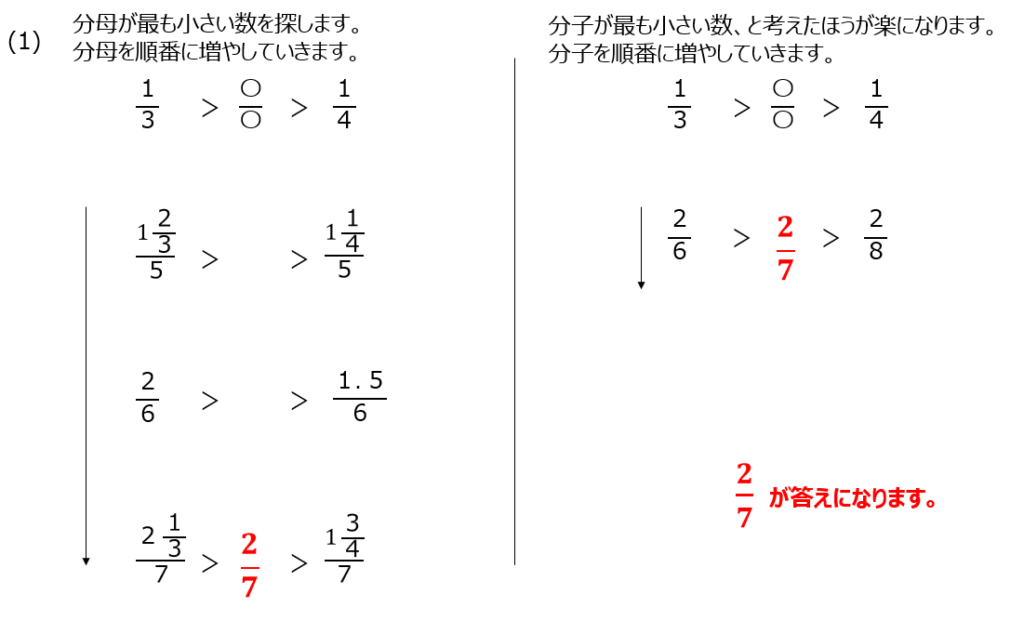
アプローチ①右1⃣
(1)分母が最も小さい数ですが、分子が最も小さい数、と読み替えてとくと簡単になります。
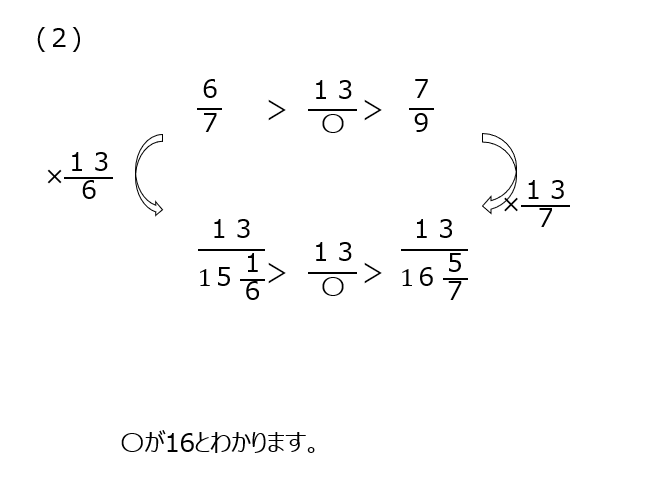
(2)分子を13にそろえるために、何倍にするか、を間違わない様にしましょう。
アプローチ①右2⃣(1)
分子を1に揃えた上で、そこから分子を2、3…と増やして考えていきます。

アプローチ②左1⃣
問題文にある、最小公倍数と最大公約数の積になる、を使って解きます。この考え方は全てにあてはまりますよ。

アプローチ②右1⃣
解法1ではベン図で考えます。動画では丁寧に説明あります。
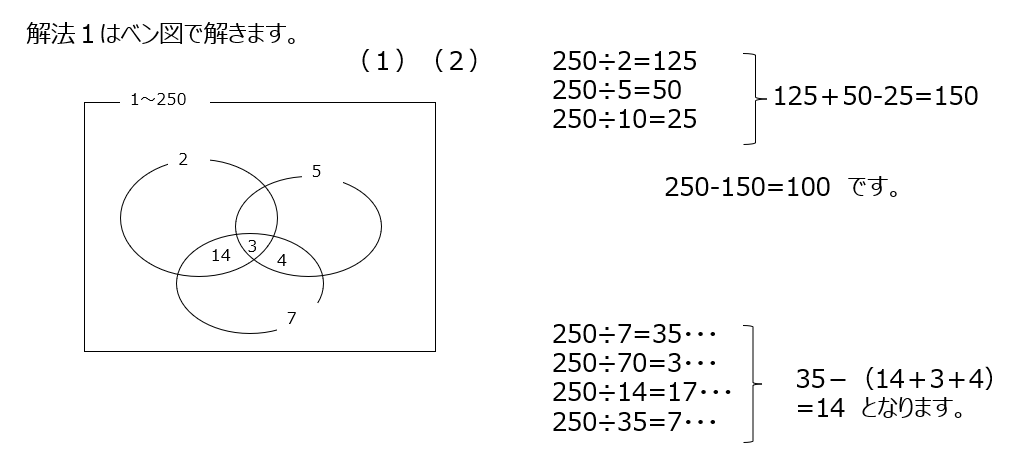
解法2では、周期を利用します。周期の場合は周期の余りにも気をつけます。補足では、より詳しく説明があります。


アプローチ③左1⃣
連除法(逆さ割り算)の形から探ります。

(2)では、2つだけで連除するパターンを考えます。

アプローチ③右1⃣
約数x倍数に注目して解きます。条件に合うものが4つ出てくるので、そのうち3つを探します。

アプローチ③右2⃣
先程と同じ問題ですが、絞り込みに工夫をしないと大変になります。素因数分解を使ってみましょう。

アプローチ④左1⃣
基本問題で解いた様な考え方です。まずは分子を1にして考えます。

アプローチ④右1⃣
小数第何位か、を聞かれています。分母を、100や1000などにすればすぐ分かりますので、この方法で進めましょう。


アプローチ⑤左1⃣
分子と分母の候補をあげて、ふさわしいパターンのものを選びます。

アプローチ⑤右1⃣
ベン図にまとめます。100個、は無作為に選んだ数字、となりますよ。
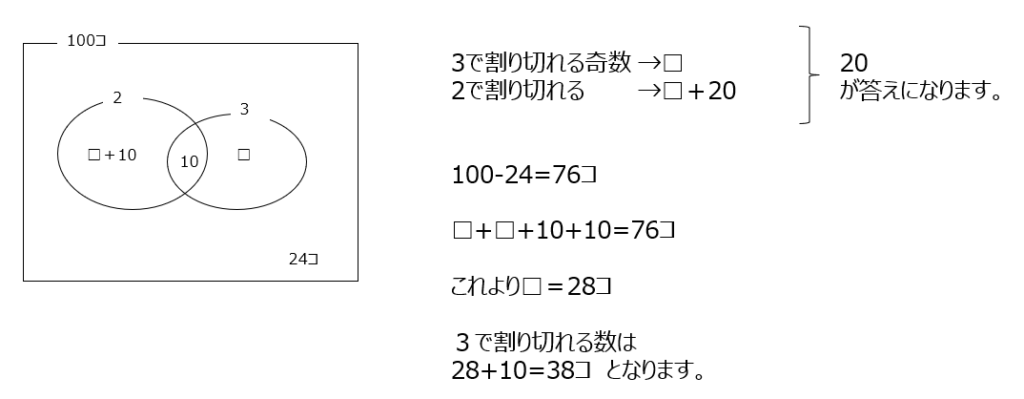
アプローチ⑥左1⃣
(1)3で初めて割り切れなくなる、なので、求めた答えに1を足します。
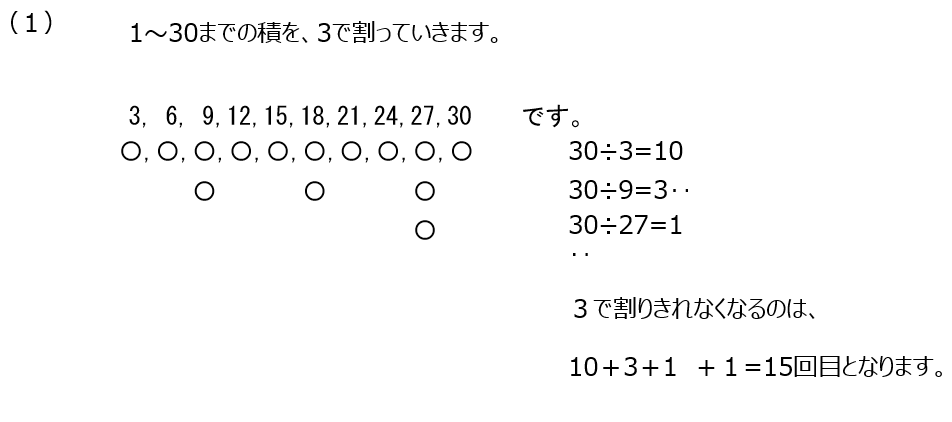
(2)2と5のうち、5の数を数えて出せます。

アプローチ⑥左2⃣(1)
3が何個あるかを数えます、その後に9は3を2個消費するので、2で割ります。

アプローチ⑥右1⃣
周期を利用して解きます。15まで周期で考えます。

アプローチ⑦1⃣
ベン図でも良いですが、周期を利用した方が計算も楽かもですね、動画では、周期の解き方でわかりやすく説明あります。
アプローチ⑧1⃣
掛け算した最後の数を考えます。10を省いて考えていきますね、なかなか難易度上がってますね。
まとめ
数の性質は最小公倍数、最大公約数、素因数分解、といった手法を使っての解き方のため、嫌いな人も多そうです、、、、とは言え、算数の基本になりますので、しっかり食らいついて進めましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント