算数の動画「平面図形総合」を見ました。
全体的に難易度は高めですかね、補助線引いたり、長さの比や面積比を用いたり、相似を使ったり、と今までの知識をすべて使います、、、6年生の後半戦に入ってきたんでしょうか、しっかり学習しましょう!

図に問題文で与えられている値を書き込んで、分かる部分を追加で書き込んで、と解き進めて、解答に近づけると良いのですが、、、、なかなか難しいですね。
導入と基本③2⃣
5年生で習いましたね、底辺と高さの比で求めていきます、周りの三角形は真ん中の三角形①に対して⑫となります、最後に中心を足すのを忘れないようにして、全部は㊲、となります。
導入と基本③3⃣
影の長さです、これも5年生で習いました。棒1mのとき、2mの影ができるので、棒:影は1:2として考えます。答えが5.5mと間違えた方はいますか?そういう人は、4mを高さにして直角三角形を考えた方でしょうか。求める三角形は、高さが4.5mを用いて考えます。どこの直角三角形を使用するかを間違わないようにしましょう。
導入と基本③4⃣
影の長さなので上記とよく似た感じです、どの三角形を求めるか、がカギです。1m:1.5mの比を用います、2:3にして考えます。影の長さ12mを使って解きましょう。
アプローチ①左1⃣
周りの三角形を引いて、答えを求めます。
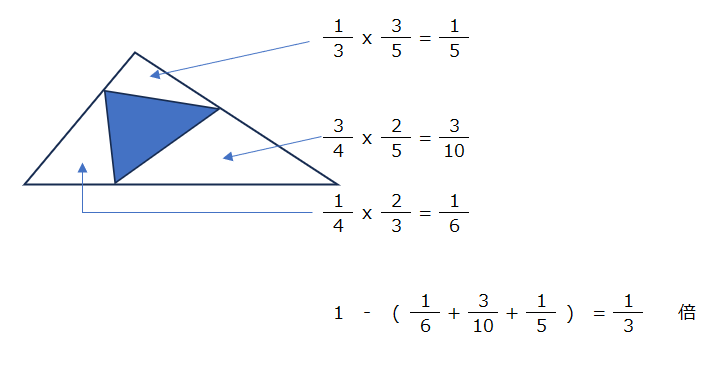
アプローチ①右2⃣
上の問題と同じですが、三角形が3つ重なって見えますね。動画で説明有りますが、同じ比になっていることに気が付くと、早く解けます。
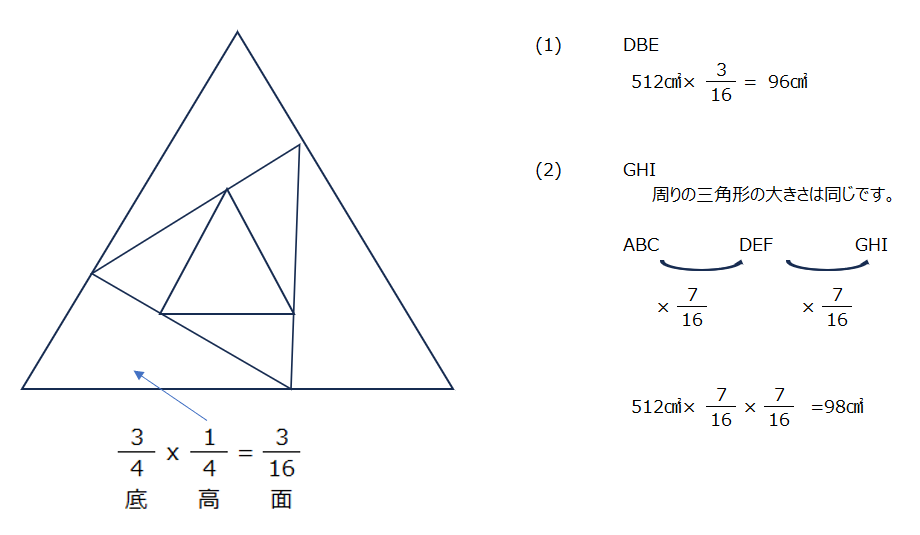
アプローチ②左1⃣
二等辺三角形を用いるのと、三角形の外角を上手く使って解いていけます。図に同じ長さの部分を書き込みましょう。
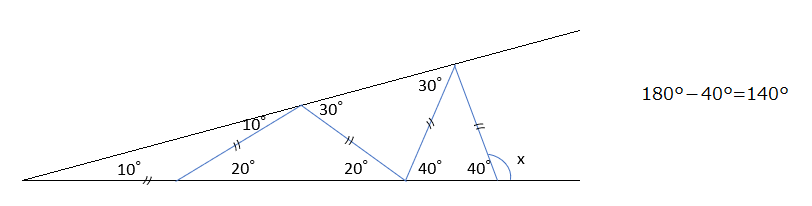
アプローチ②左2⃣
xを①として、外角を算出していくと解けますよ。動画は分かりやすいですね。
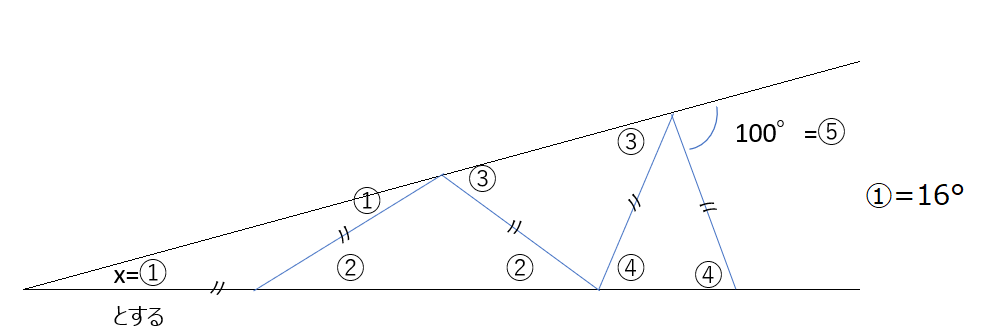
アプローチ②右1⃣
長さと面積の式を書いて、それを比較して考えます、3.14は必要ないですよ、、、、中心角をもとめる必要はありません。別の考え方として、細かく切断して考える方法があります。これは以降でも使う考え方なので、是非とも動画で確認しておきたいです。

別の解法では、細かく切って考えます。
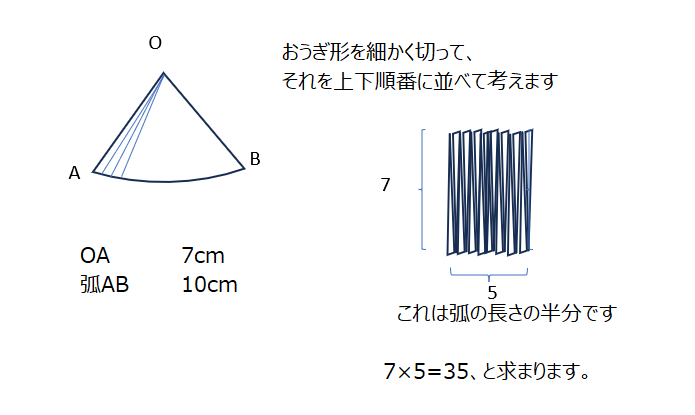
アプローチ②右2⃣
細かく裁断して、長方形で考えます。弧の長さは弧MNの2倍の弧ABは10cmです、先ほどの問題と同じ様に長方形で考えると、5×8=40、と求まります。動画では、もともと弧MNが分かっているので下記が5cmとわかる説明を加えてくれていますよ。
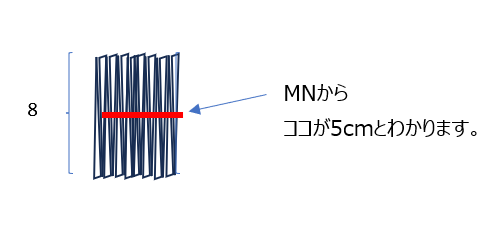
アプローチ③左1⃣
折り曲げた図です、折る前の図も書いてみると分かりやすいです。同じ角度、同じ長さを考えます。錯角と折った角、からどこが同じか、を書き込みましょう。外角104°の半分がアの角度、とわかります。
アプローチ③右1⃣
長方形を重ねます、重なったところを求めます。2つの長方形から重なった部分を引く、という考え方です。重なったところはひし形になっています、考え方は動画で詳しく説明がありますよ。
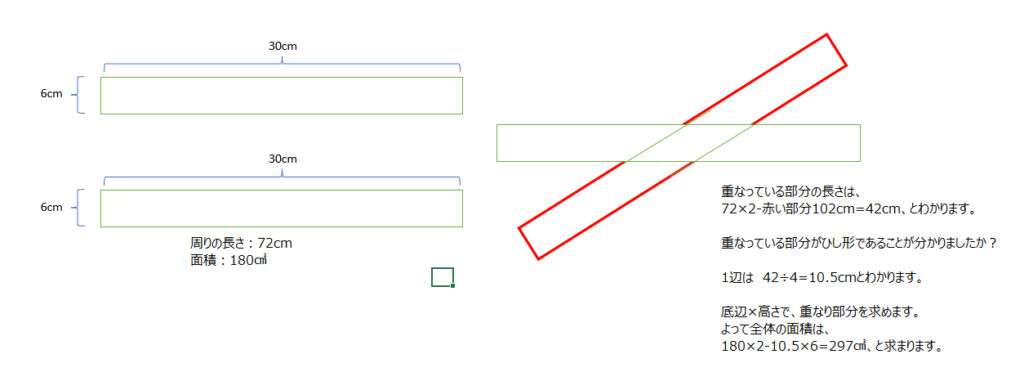
アプローチ④左1⃣
きれいな図ですね、正六角形の性質は、土特で習いましたね。面積はどこからどこを引くかです。円周率は3.1ですよ、間違えないように、、、、、
(1)正六角形は6等分されていることが分かります。173.2×6÷4で求まります。(2)斜線以外の白い部分(半径10cmの円)に注目すると、全体から半径10cmの円を引きます。全体は正六角形+半円6個です。注意は、円周率が3.1ですので、まずは式を書いてから計算に取り組むようにしましょう。259.8+5×5×3.1×½×6コ - 10×10×3.1=182.3㎠、となります。
アプローチ④右1⃣
斜線の部分を求めます、おうぎ形に分けて考えていきます、きちんと線を引いて切り分けていきましょう。それぞれのおうぎ型の中心角を間違えないようにします。
真ん中の正方形は1辺6cmです。四隅の大きいおうぎ形の中心角は、360-(60×2+90)=150°です。小さいおうぎ形は中心角60度です、これが8個あります。半径は6cmですべて同じなので、中心角の和を出すと、150×4+60×8=1080°です。円周率は「3」なので、6×6×3×(1080÷360)=324、となります。
アプローチ⑤左1⃣
立体図形ですが、考え方は平面です。横から見て、ピラミッド形になっている相似の三角形比で解いていきます。
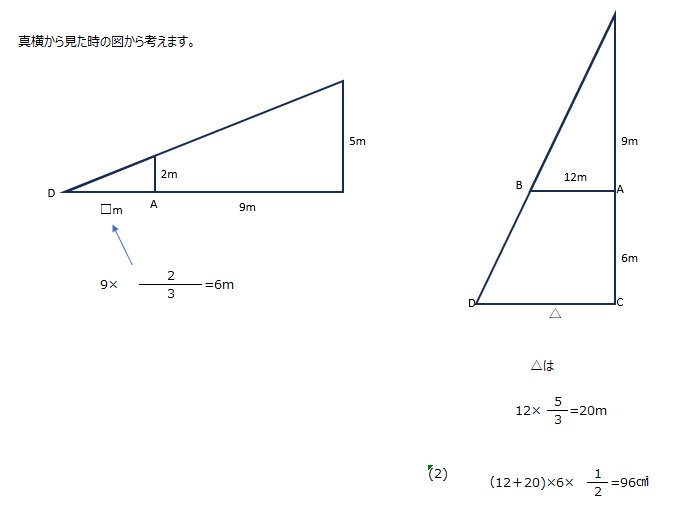
アプローチ⑤右1⃣
斜線の部分と全体の面積の割合を求めます、真ん中の斜線部は平行四辺形です。斜線部分の分ける底辺の比、で考えます。全体的に見て、どこに相似となっている三角形があるか、を見つけていく作業ですね、ピラミッド型の相似の三角形を上手く探せるか?です。
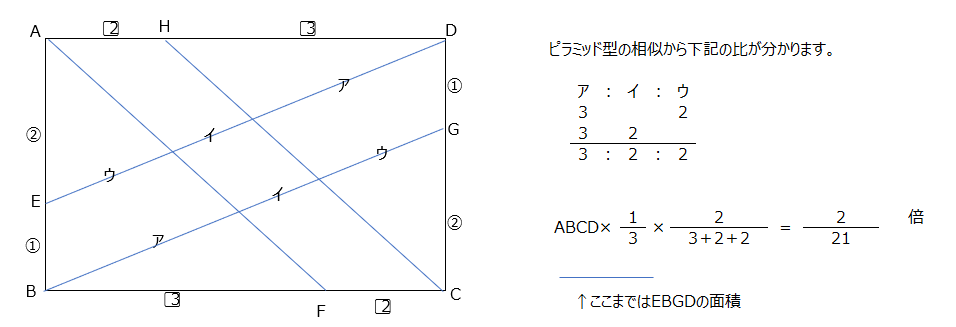
アプローチ⑥左1⃣
正方形の1辺を1とし、各長さがどれくらいの割合になっているか、を求めて解きます。1辺を60と置いても解けますが、計算が大きくなります。分数の計算になりますが、頑張りましょう。全体1から斜線の部分を引きます。
アプローチ⑥右1⃣
解法1では、1辺を1として計算していきます。同じ面積があるので、求めるのは二種類の斜線部、と判断します。砂時計型の相似から辺の比を求めて計算していきます。なかなか気づけないかもしれませんので、動画での確認をお勧めします。
解法2では、補助線をBから縦に垂直におろして引いて、面積比で計算していきます。これも難しいですが、動画では丁寧に説明があります。
アプローチ⑦1⃣
横からの図で考えます。(1)(2)(3)では影ができる三角形の違いがありますが、考え方は同じですね。図に書き込んで考えていきましょう!
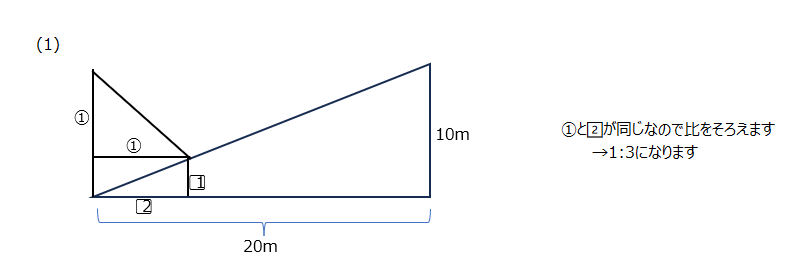
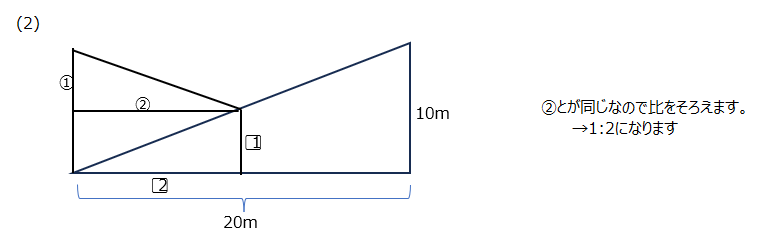
(3)上の(1)(2)の考え方を用います。比をそろえると旗:AH:BI=6:2:3から求まります。
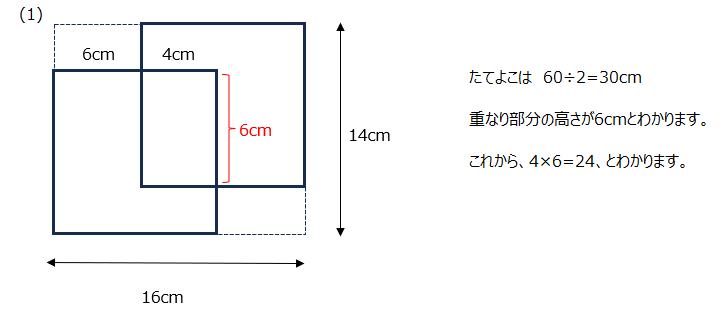
アプローチ⑧左1⃣
重なる正方形です。全体の長さと1辺の長さから、重なっている部分の長さが分かります。動画で確認しましょうね。
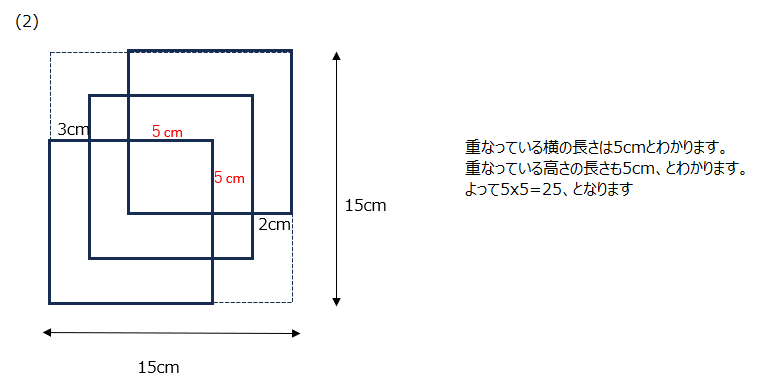
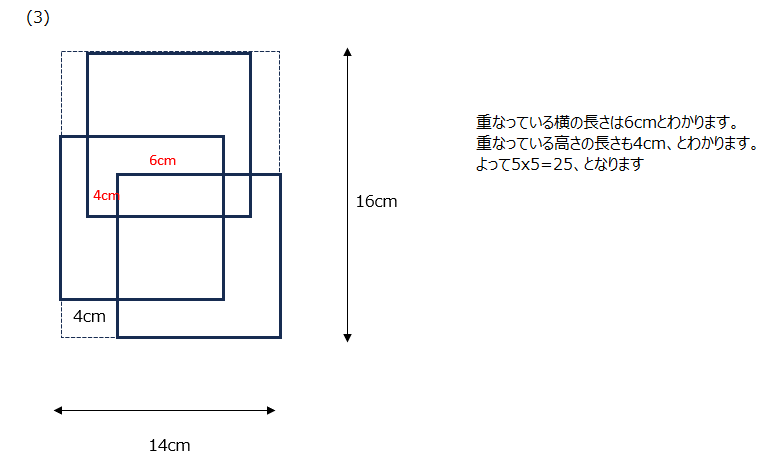
アプローチ⑧右1⃣
方眼になっています。大きな四角形から周りの三角形を引く方法もありますが、動画では内部底辺を求めて考える方法で説明があります。どこを底辺とするか、高さはどれか、方眼の1方眼以下の部分がいくらか、そのあたりが大切になります。動画では分かりやすく教えてくれています、いろいろな解法をおさえておきましょう。
実戦編A2⃣
斜線部分を移動させると分かりやすくなります、計算が楽になりますね。

実戦編A4⃣
円の小さい部分を移動させてると分かります。

実戦編E2⃣
解法1では(1)の答えを用いて、全体から2種類の三角形を4つずつ引きます。動画では色を付けて説明していて、とても分かりやすいですね。
解法2も聞いておきましょう、補助線を真横と真縦、に引いて、4つに区切って考えます。なかなか難しいですけど頑張って聞いてみましょう。
今週の立体切断1⃣
三角錐からとがってる先を切り落とします。切り落とすと、辺、面、頂点が、どういう変化をするか、増えるか減るか、などを、理解しましょう。(1)全体の体積と切り取る1つの体積の体積比は、1:27になることを確認します。(2)元々は、辺6つ、麺4つ、頂点4つでした。切り取ると、麺は4つ増えて8つになります。辺は3つ×4=12つ増えるので、6+12で18つ、となります。頂点は4×3=12つ、となります。(3)でも辺と面のから考えます。動画では展開図の1例を用いて説明があります。ただ、展開図を書くのは難しいので、面が8つあることから、7本の辺がつながっている、と、これから解くように説明があります。
今週の立体切断3⃣
はじめに12面体について整理しておきます、動画ではキチンと説明があります。画面がズームインされて分かりやすく説明があります。図から数えるより、計算で出せるようにしましょう。なかなか考え方が難しいですが、動画での説明が分かりやすいので、確認してみましょう。
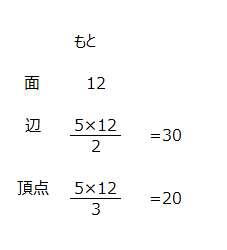
まとめ
ピラミッド型と砂時計型の相似を上手く見つけれるようにしたいですね。全体的な解き方として、問題の図に分かる値を書き入れて、それから分かるところを追加して書き入れて、、、と解き進めて、どこかで気付けるか、になりますでしょうか。数を沢山こなして対応しておきたいですね、頑張りましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント