算数の動画「数の性質(1)」を見ました。
数の性質は何度も出てきていますね、得手不得手が分かれる所でしょうか。。。苦手意識はもったいないので、得点できるように頑張りましょう。

夏期講習の最初です!頑張っていきましょう!!
導入と基本②3⃣
最小公倍数を求めますが、問題文から1番小さい数を求めますよ
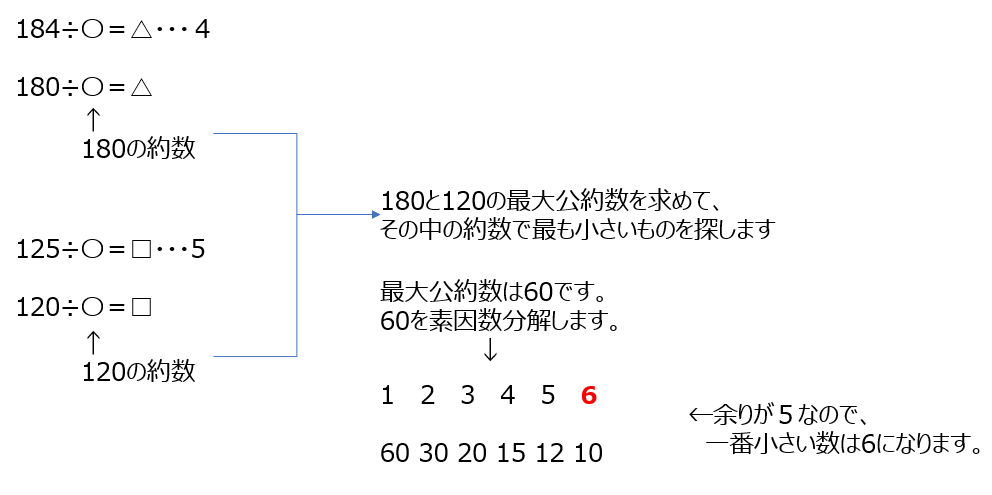
アプローチ①1⃣
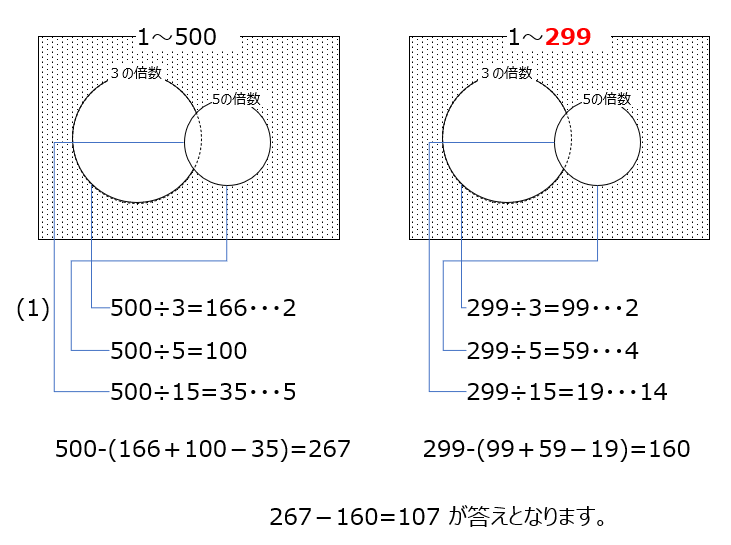
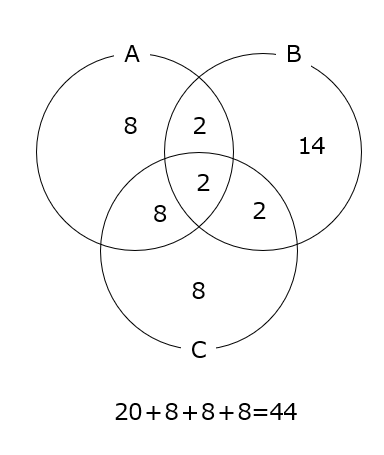
ベン図で考えます。1~500までを調べて、その後に1から299までも考えて、引き算すると、300から500の答えを出すことができます。
(2)余りが無ければ、と考えます。(12と20の公倍数)+1、です。ので60の倍数+1=で、120+1、で求まります、最小公倍数で求めます。(3)余りが違いますのて、考え方を変えて解きます。書き出して考えます。書き出して1番小さい数を出します、「31」と分かります。次は、4と9の最小公倍数36を足した「67」、となります。つまり、31+36×□≒999くらい、を探します。
(4)は線分図で解きます
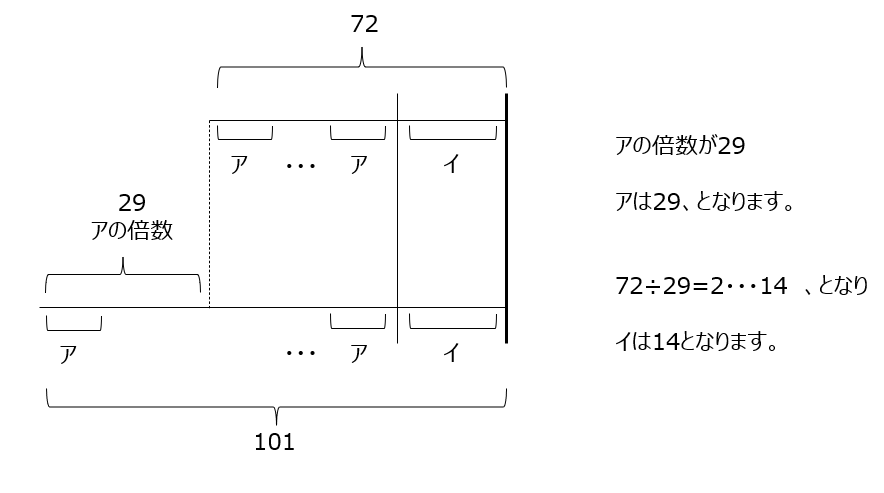
(5)分子を操作します。最小公倍数の分母で考えて、分子の差を求めます。
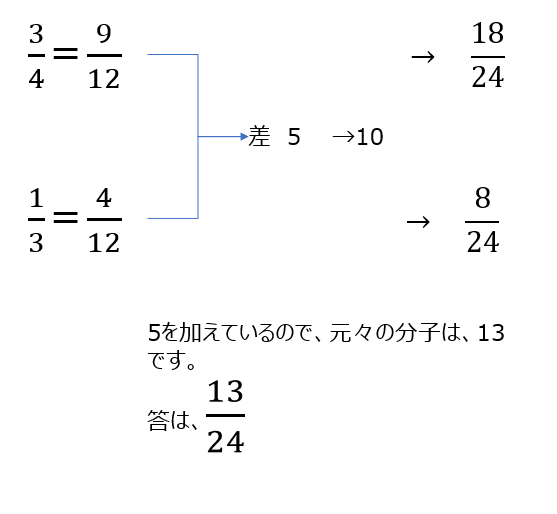
導入と基本②2⃣
それぞれあと4あれば割り切れます、ので、最小公倍数より4少ない数、を求めます。
(9,12の最小公倍数36)-4=32です。36×2-4、と考えることができます。つまり、36×□-4≒999くらい、とすると、□は27となり、968となります。
アプローチ②左1⃣
(1)既約分数です。
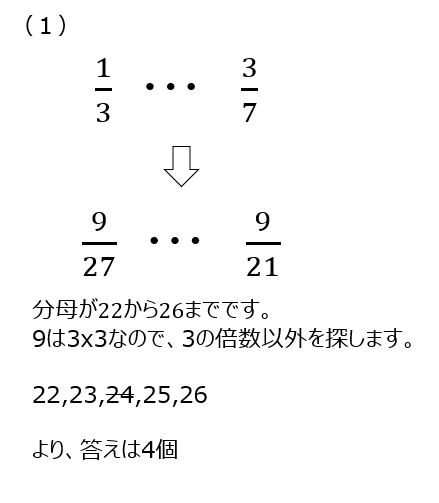
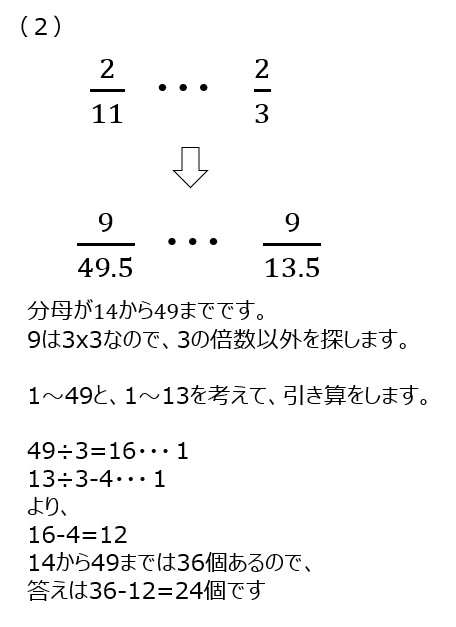
(2)では分母か14から49で考えます。49までから、13まで、を引く考え方です。
アプローチ②右2⃣
(1)では書き出して考えます。計算で求める方法も説明あります。2の倍数が18÷2=9個、3の倍数が18和r3=6個、18÷6=3個、より、18-(9+6-3)=6個、と求めることもできます。2個を足すと1なので、答えは3,となります。また、周期性からも考えれます。(3)(4)は帯分数で考えます。動画での説明を確認してみましょう。
アプローチ③右1⃣
書き出して最も小さい数を求めます。そこから24毎増やして求めます。

別解では線分図で考えます、12の倍数は8の倍数でもあることが分かります。つまり、24の倍数+6なので、30,54,78、と求めることも可能です。
アプローチ③左1⃣
線分図で考えます。動画ではわかりやすく解説あります。
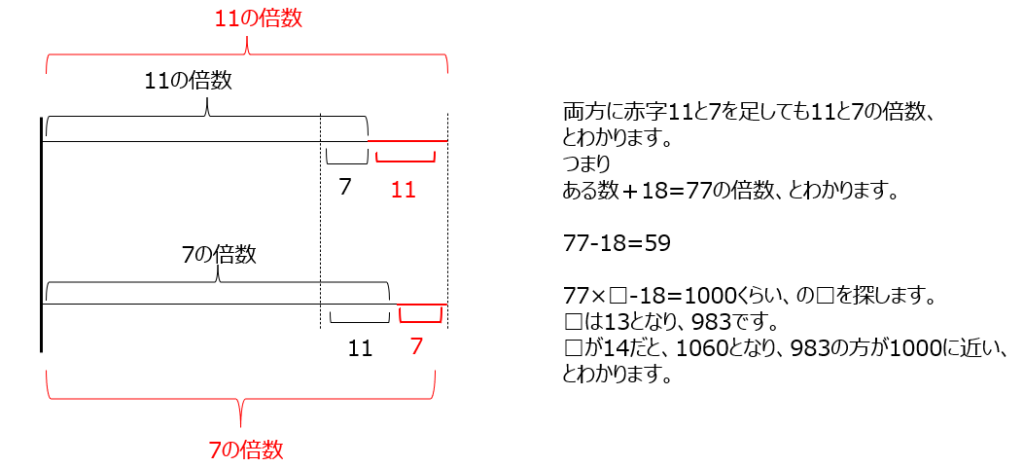
アプローチ④左1⃣
動画では式にして、当てはめながらの説明があります。あまりの数に気をつけて当てはめていきます。
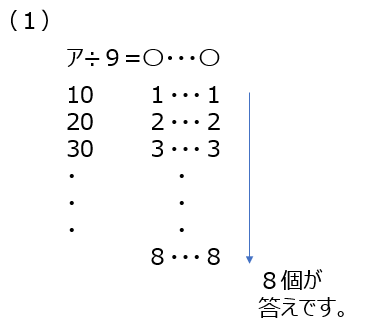
(2)は最後にあまりの数を数える事で問題が解けます。

アプローチ④左2⃣
先程と同じ様に考えます。問題文をきちんと読んで答えないと、間違えるパターンです。

(2)では200まで、を考慮しましょう!

アプローチ④右1⃣
比べて差を求めて進めます。AとDの差が4,BとCの差が1,と分かります。これより、ABとCDの差のパターンは、(1,2)か(2,1)か、の2パターンです。偶数奇数などの考え方から絞られます。
ABの差が1,CDの差が2とすると
A,Bの和88,差は1なので、答えが整数にならないです。
ABの差が2、CDの差が1とすると、
A,Bの和88,差は2となり、(88+2)÷2=45と、答えが整数になり、正しいです。
これより、Aが45とわかります。
アプローチ⑤1⃣
花火の打ち上げる時間がズレてます。揃って時の最初がゼロです、そこから始まります。ベン図で考えるとわかりやすいですね。

オはベン図を書いてみます。
アプローチ⑦左1⃣
(1)円の中で跳ね返ります。45°だと4回跳ね返って元も戻ります、キレイな正方形です。(2)50°で跳ね返りますが、中心角80°について考えます。80°と360°の最小公倍数で考えます。前の問題では中心角が90°でしたので、360°との最小公倍数は360なので、360÷90=4、と計算で求めることもできます。この問題では、80と360の最小公バイスは720です、720÷80=9回跳ね返って、元に戻ることができます。
別解では(1)では90°ずつ、つまり、4分の1ずつズレると考えて、整数になるタイミングを考えて解く方法です。(2)では9分の2ずつずれるので、9回でちょうど2周する、と分かります。
アプローチ⑦右1⃣
40本の杭が池の周りに打たれていて、ペンキを塗ります。(1)Aを塗って、7本ずつ進んでペンキを塗ります。二週目は7×6=42なので、42-40=2本目が二週目、となります。7と40の最小公倍数280です、つまり280÷40=7周まわった後、となります。280÷7=40回すすんだ、となりますので、すべて塗った、となります。別解では、40分の7ずつ増えていく考え方です。この考え方で次の問題も解きます。(2)40回以上塗れるか、考えます。

アプローチ⑥左1⃣
8分割して進んでいきます。動画では図に書いて分かりやすく説明してくれます。12分割でも説明あります。最終的には図を書かずに解きます。動画は下記コメントがありますよ。
ここまでしつこくやったので、完璧に理解できましたよね?その確認として、アプローチ⑥右1⃣を解いてみましょう!(解説動画はありません)
アプローチ⑧1⃣
先程の考え方の応用です、内側と外側、と2つあるので、考え方が難しくなります。(1)12秒ごとですので、13で発光するのが12×13=156秒後、です。外側は156÷5=31あまり1です、ので、次に着くのは32番、となります。(2)60秒ごとに青と赤は同時に発光します。その時の番号を書き並べてみます。青は12,24,36,6,18,30・・・・となります。赤は5,10,15,20,25,30・・・となり、30で同時に光ります。つまり、一週42のうち30進んだところで発光する、つあり、全体の7分の5進んだところで発光します。つまり、42を7等分したところなので、42÷7=6、答えは6,12,18,24,30,36となります。結構難しいので、動画で確認してみましょう。
まとめ
ベン図をかいたり、線分図にしたり、自分で分かりやすいように解いていくことが大切ですね。動画でも丁寧に説明してくれていますので、分からないところは見直すようにしたいですね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント