算数の動画「文章題総合」を見ました。
総合的な問題ですが、今までの知識を使えば何とかなる問題な感じですね。比や逆比、仕事算、など至れり尽くせりですが、問題内容を図示化して、自分なりに頭の中で整理して解き進める、という基本スタンスは変わらないですよ。

力まずに、問題文の理解することを頑張りましょう!
導入と基本①1⃣(5)
枚数の比からそのままの合計金額を出してみます。実際の合計金額から、何倍かを考えて答えを出します。

導入と基本③1⃣
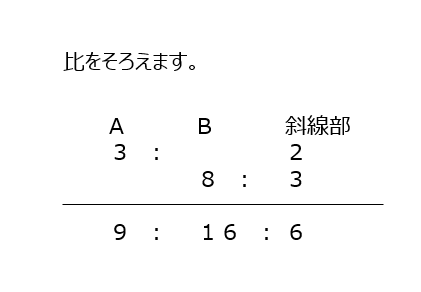
AとBと斜線部の比を揃えで解きます。
導入と基本③4⃣
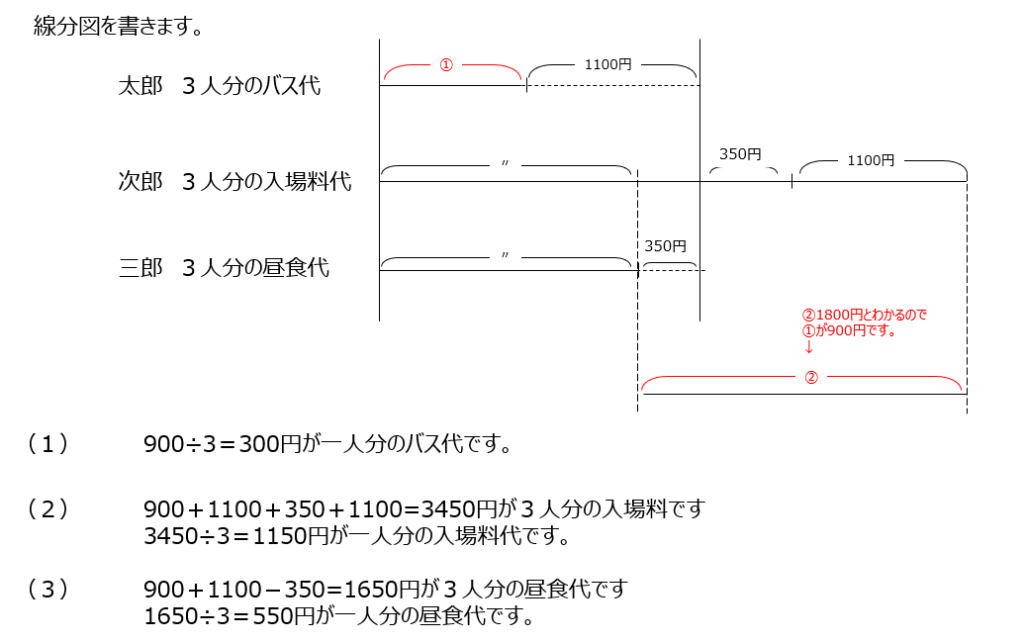
太郎と次郎と三郎が、バス代と入場料と昼食代を払った問題です。線分図にまとめます。3人分で計算しています、答えるときは1人分で聞かれているので気をつけましょう。
アプローチ①1⃣
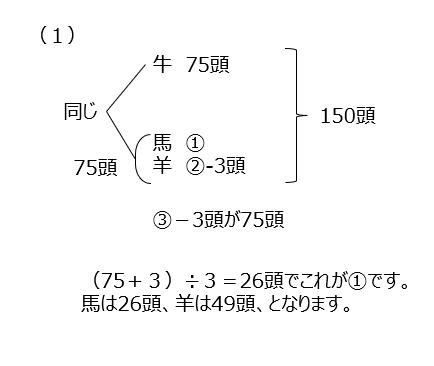
(1)牛の頭数はすぐ分かり、馬と羊も割合で解けますね。
(2)AとBとCです、AとCの比から解き始めます。

(3)これも同様ですね、AとBの比から解き始めます。

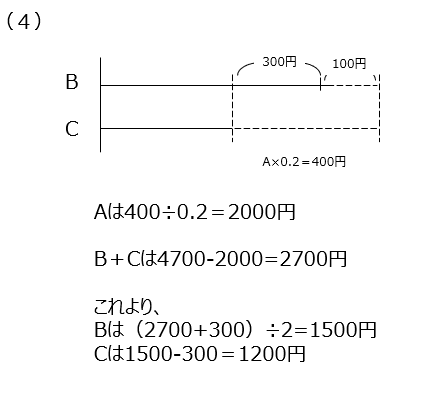
(4)線分図でAとBとCの関係を表します。
(5)兄と弟の金額を比で表します。動画では、丸と三角の比を、差をとる事で揃えています。

(6)もらった比と使った比で二つ式を書きます、消去算をします。

アプローチ②左1⃣
図にまとめると分かりやすいですね、使う前のお金の合計を比で表して解きます。


アプローチ②右1⃣
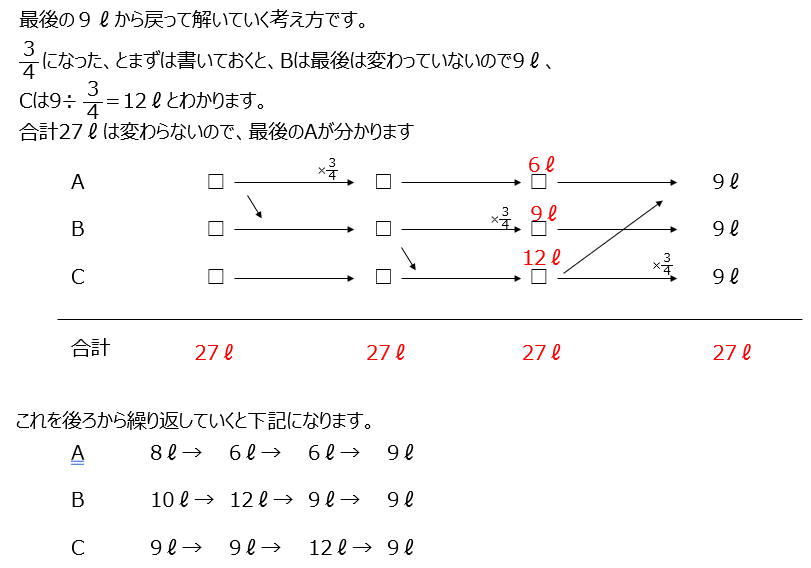
水のやりとりです。最後から遡って考えるようにします。この手の問題はあげた4分の1よりも残った4分の3の方が大事ですので、それを記載する図にしましょう。また、合計の量も変わりません。
アプローチ③左2⃣
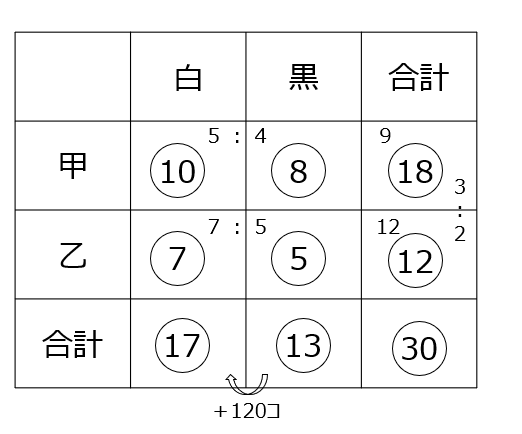
たくさん比が出てきますが、全てを揃えて考えます。動画の様に表にまとめましょう。

アプローチ③右1⃣
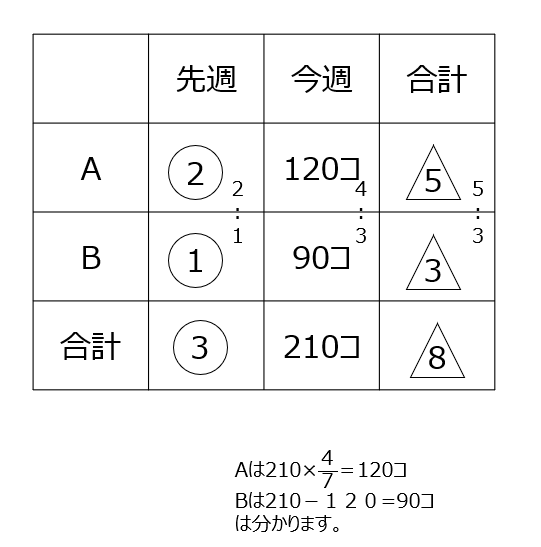
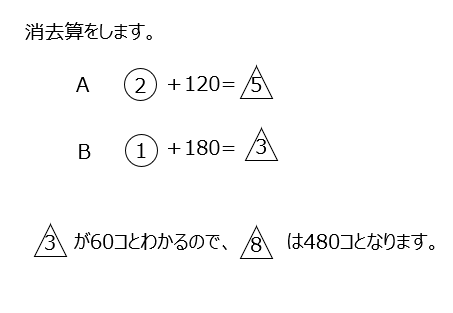
今週と先週と合計、の比が出ています。具体的な数字のある今週からAとBの数値を入れ、そのあとは消去算になります。
アプローチ④左1⃣
AとBの操作をします。Aは和が-8個で差が変わらないです。Bは和は変わらないですが差が2個変わります。(1)と(2)は操作が1種類なので操作の特性から比で解けますね。(3)は和からでも、差からでも解けます。(4)は最後の個数はわからないですが、同じになったので、差の変化するBの操作の回数がわかります。





アプローチ④右1⃣
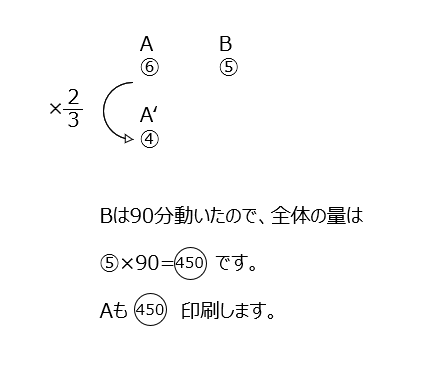
仕事算になります、Bから全体の仕事量が出るので、Aが速さが変わる前後で何分かかったかを出します。(2)では仕事量からつるかめ算をしますが、聞かれている値に注意しましょう。

アプローチ⑤左2⃣
逆比を使ってAとBの所持の比を出し、それぞれの減った後の差から、実際の量を出します。

アプローチ⑤右1⃣
AとBの身長が現在は同じという問題です。2年前のそれぞれの身長に伸びた分をかけると現在の身長になるので、式を書いて逆比を使います。

アプローチ⑥左1⃣
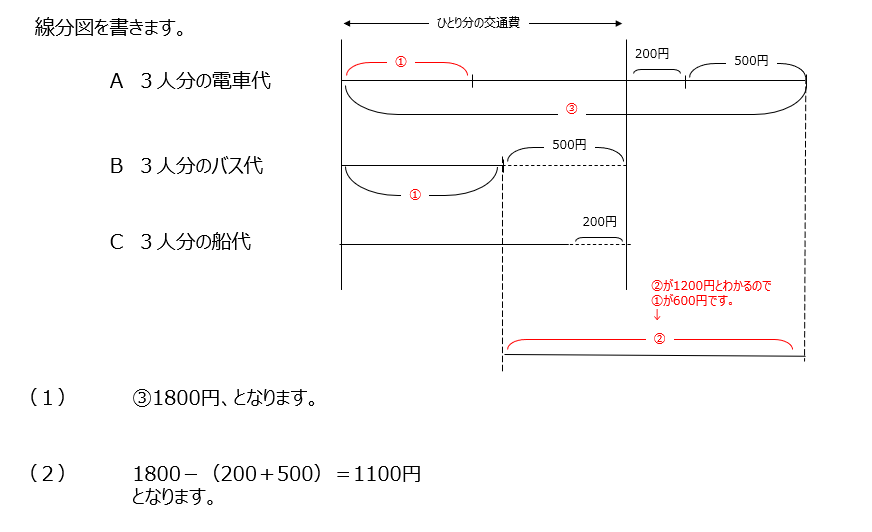
3人分の電車代、バス代、船代の問題です、導入と基本でもありました。3人分まとめて計算しているので、答え方には注意しましょう。
アプローチ⑥右1⃣
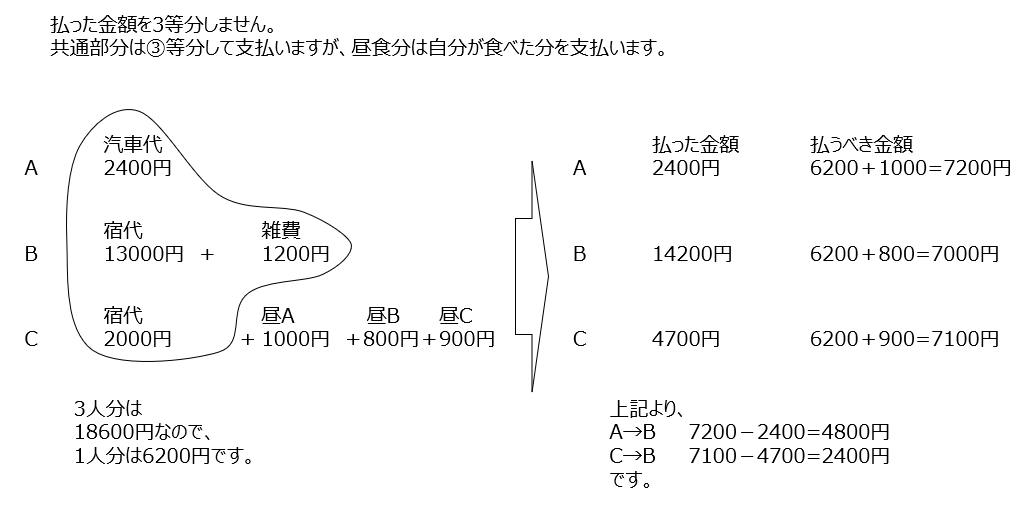
3人の汽車代宿代雑費代にそれぞれの昼食代が加わっています。昼食以外は3分割して、それにそれぞれの昼食代を足して払うべき金額を求めます。
アプローチ⑦左1⃣
AとBの巻尺の問題です。各巻尺何個分か、の逆比から、AとBの巻尺の長さの割合が出ます。その差が正しい長さの30cmなので、それより、各巻尺の正しい長さが分かります。

アプローチ⑦右1⃣
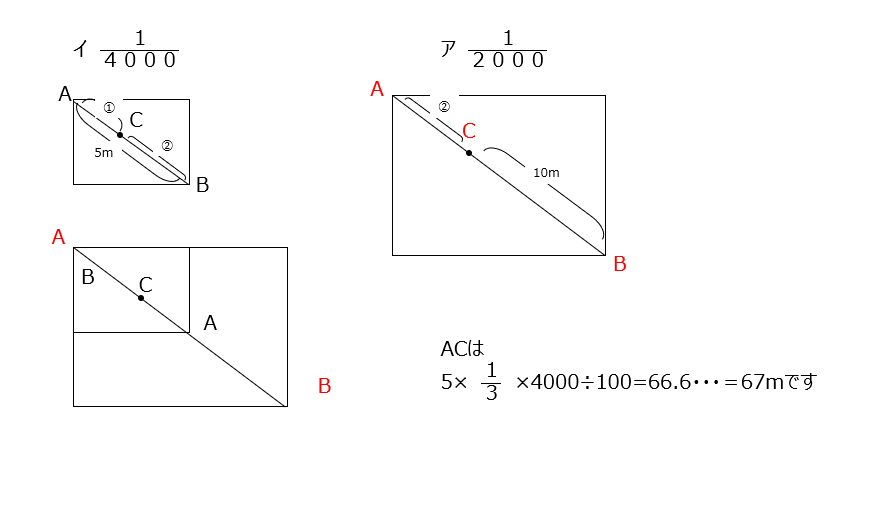
縮尺の違う地図をクルッと回転させて重ねます。重なるCは対角線上しかあり得ません。Cが対角線の何分の一かを求めます、縮尺の違いと回転さした事を考慮します。詳しくは動画の説明がわかりやすいですね。
アプローチ⑧左1⃣
面積と人口の比から人口密度を考えます。人口密度は、人口の比÷面積の比で求めます。比の計算をして人口密度を比で出します。

アプローチ⑧右1⃣
年齢の比でもらえる枚数が変わります。ABDとCの比は、5年後も今の比と変わりません。

アプローチ⑧右2⃣
3人の使った金額と残った金額の比が分かっています。合計の比から、4分の1にするとBの金額が分かります。

まとめ
文章題総合なので、さまざまな問題が出てきますが、線分図にしたり表を書いたりして、問題理解を充分にすることが大切に思います。まとることができれば、そこからひらめきに繋がりそうです。サボらずに図示する事を毎回しましょう。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント