算数の動画「数の性質」を見ました。
何度も学習してきた数の性質です。回数を重ねるごとに手を変え品を変え、いろんな角度から問われてます。でも、基本的には、約数、倍数、素因数分解、などを駆使して解くので、基本を大切にして、数をこなして経験値でカバーをしたいですね。

夏期講習明けの9月から心機一転、頑張りましょう!
導入と基本①4⃣
数を分解して解きます。出てくる各数字の関係を式にし、各条件から求めましょう。

アプローチ①1⃣
組み立て割り算(すだれ算?連除算?)で解きます。一部の数が分からなかったり、問題で条件が与えられていたり、といろいろな形で問われています。AとBが複数個あり得る時も、問題文の条件を確認して、それぞれの数を当てはめまてふさわしい数字を求めます。




アプローチ②1⃣
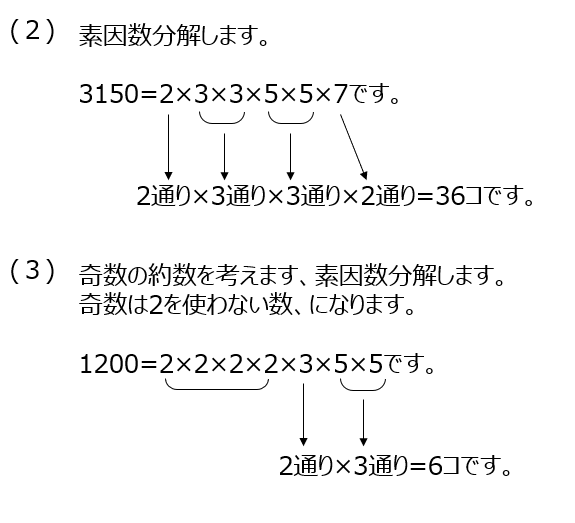
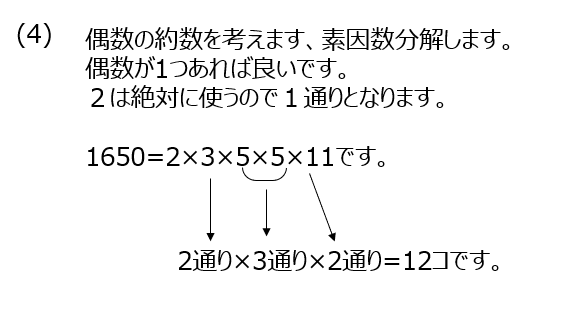
約数の個数の求め方は、素因数分解して考えます。素因数分解の後に表にして考えると分かりやすいです。(2)以降では、素因数分解した形で問題を解いていきます。全部の約数の個数も計算で出せますね。約数のうち、偶数だけ、とか、奇数だけ、は、素因数の2を含めるか含めないか、になります。


アプローチ③左1⃣
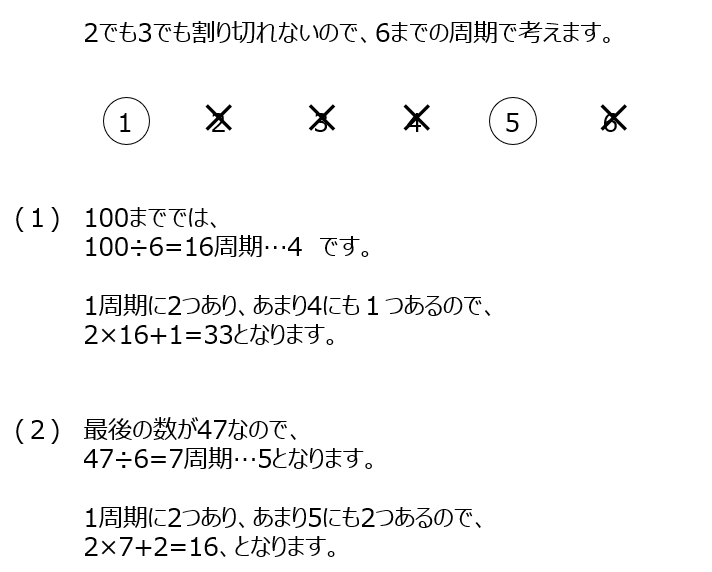
周期を利用して解きます。6までが1周期で、余りを考えて解きます。
アプローチ④左1⃣
AとBの和が88とわかっているので、11で割った数の和は8になります。そこから場合分けして解きます。

アプローチ④右1⃣
2で割り切れる回数を求めます。素因数分解して、2がいくつあるか、です。100より小さくて、2で3回割れるので、8の倍数になります。気をつけないといけないのは、100より小さいから、8×12とすると、2で3回以上割れるので、12ではダメですよ。(3)でも、掛ける範囲から、個数を求めます。


アプローチ⑤A1⃣
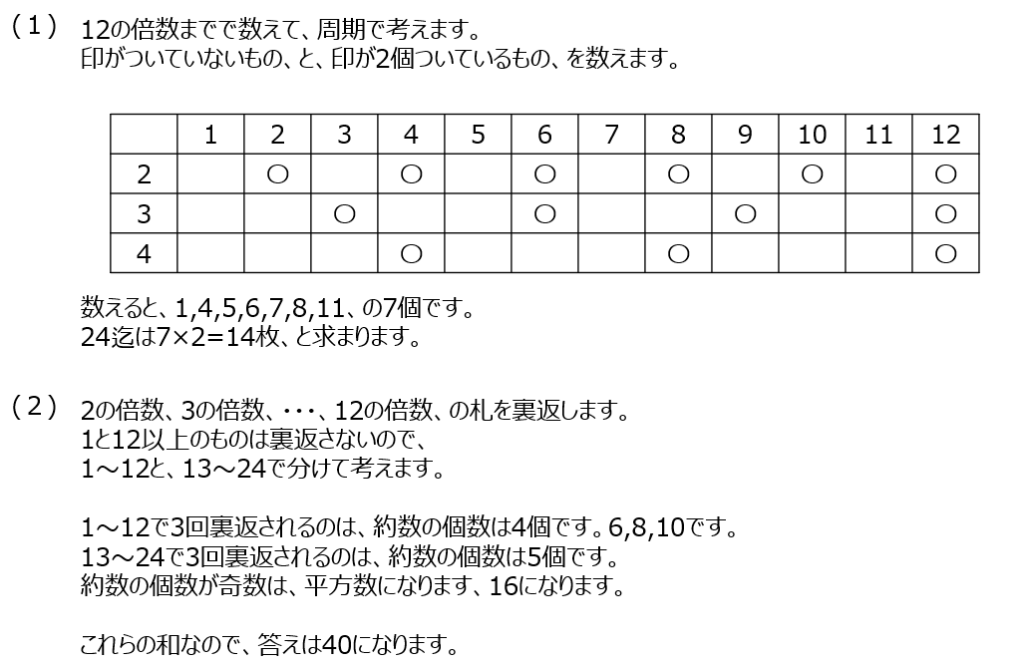
カードをひっくり返します。対象となる数の1を除く約数の数だけ、ひっくり返します。(3)では、約数が奇数個のものを探します、つまり平方数のものを探します。



アプローチ⑤B1⃣
先程と同じようにカードをひっくり返します。動画では表に書いて説明あり分かりやすいですよ。次の問題では12までと13以上で二つに分けて考えますよ。補足では素因数分解しての考え方を解説してくれています。

アプローチ⑧右1⃣
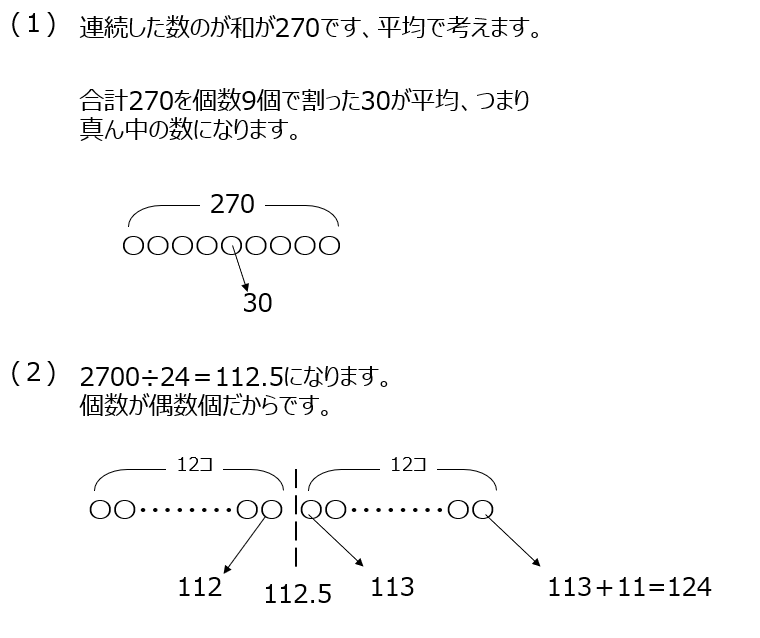
連続した数の和の問題です。連続した数の個数がわかっているので、和を個数で割って平均を求めると、連続した数の真ん中の数がわかります。連続した数の個数が奇数か偶数かで解き方が変わりますよ。
アプローチ⑥A1⃣
丸太を積む問題です、指定本数を何段で積むか、の問題です。(3)では30本が奇数段か偶数段か、の2通りを考えます。



実戦E3⃣
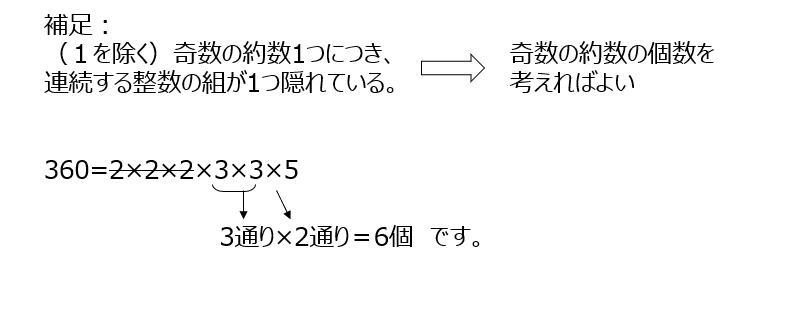
連続数の問題です。360を奇数個で割るか偶数個で割るかです、平均の値と連続個数で、あり得る場合だけを抽出します。補足として、1を除く奇数の約数1個につき、連続する整数の組が一つ隠れています。ので、奇数の約数の個数を考えれば良いです。なかなか難しいですかねー

アプローチ⑥B1⃣
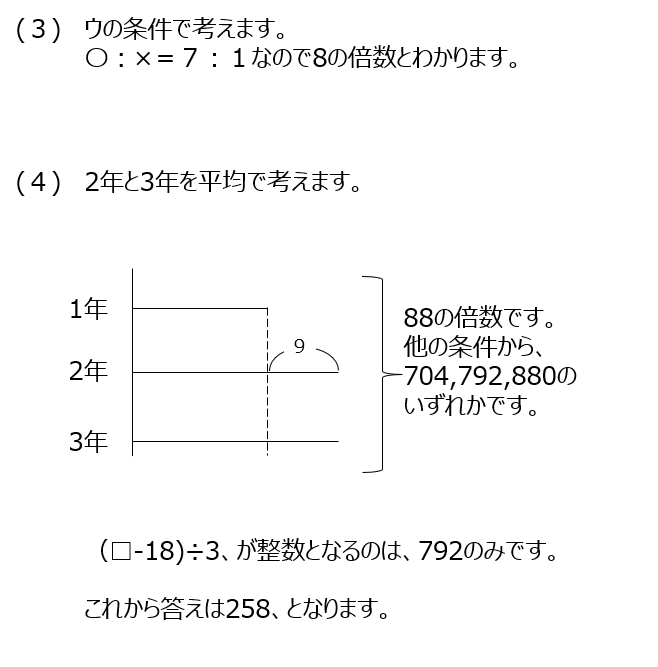
学校の生徒の数の問題です。問題を解き進めると、生徒全体が88の倍数であるとわかり、そこから解きます。

アプローチ⑦左1⃣
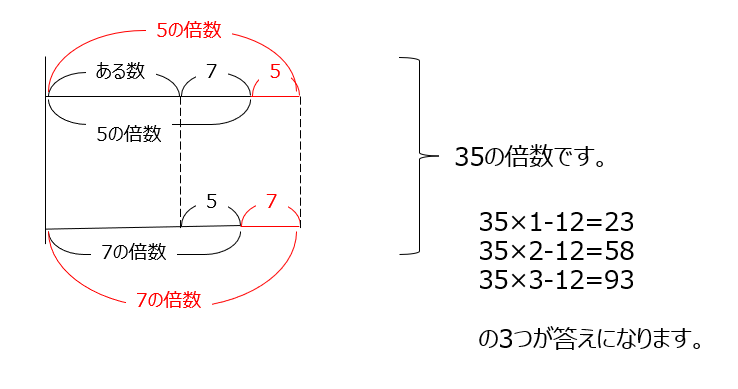
ある数を求めます、条件を線分図にして整理します。図解がわかりやすいのですが、35の倍数から12を引いたものになります。動画がオススメですね。
アプローチ⑦右1⃣
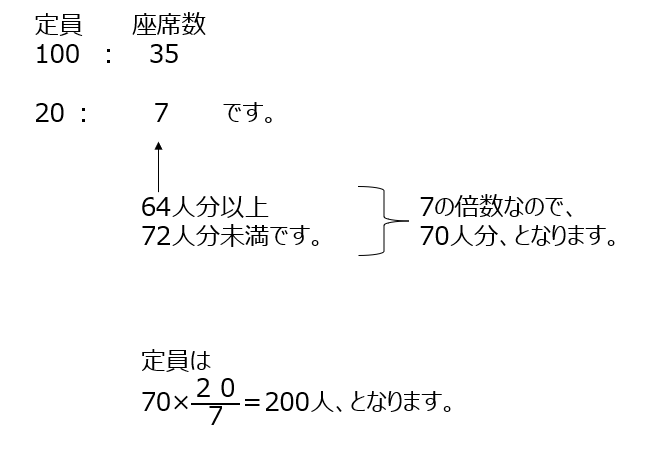
定員と座席数の問題です。比を簡単にして、座席数の範囲から、定員を求めます。
アプローチ⑧左1⃣
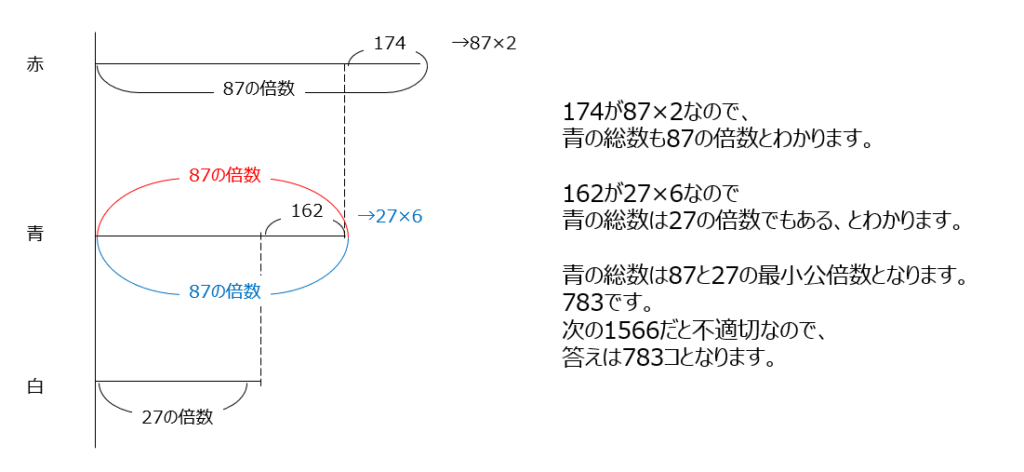
赤、青、白の数を求めます。赤は87の倍数、白は27の倍数、と分かりそこから、青を求めます。これも動画がわかりやすいですね。
今週の立体切断1⃣
基本の確認となります。切り口の線は立体の表面に出てきます。向かい合う面の切り口は平行です。三角形の相似を用いて、切り口から延長した三角すいを求めます。体積については、小さい三角すいをもとに、角にある小さい三角すいの倍率と、全体の三角すいの倍率を求めて、考えます。最後はどちらが大きいか、を調べます。

今週の立体切断2⃣
複数回の切断です。図に描くと複雑になりますし、テストでは色も変えれませんので、工夫して書きましょう。濃さや点線を利用しています。動画のやり方を参考にして練習する事をお勧めします。とても分かりやすいですよ。面と面の交わりは、線になるので、交点を結びましょう。(1)(2)では、平面図から交点の位置を考えます。(3)以降も、前の問題の答えを使って解き進めます。
まとめ
何度も学習してきた数の性質です。回数を重ねるごとに手を変え品を変え、いろんな角度から問われてきますね、、、、でも、基本的には、約数、倍数、素因数分解、などを駆使して解くので、基本を大切にして、数をこなして経験値でカバーをしたいですね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント