算数の動画「速さ(1)」を見ました。
図を書いて問題の理解をした上で解いていく、この方法に慣れ親しんだ方が、速さの問題では解きやすそうです。是非とも身につけましょう。特に比を使って解くことを当たり前のように進めましょう。

図を書いて理解を深めて、比で解くようにしましょう。
導入と基本③2⃣
父と子の歩数の問題です。歩幅は逆比で8:3です。同じ時間での歩数の比はは6:7です。これらから、父が48進む間に、子は21進みます、コレが同じ時間で進む距離ですね。答の比は簡単にしますよ。
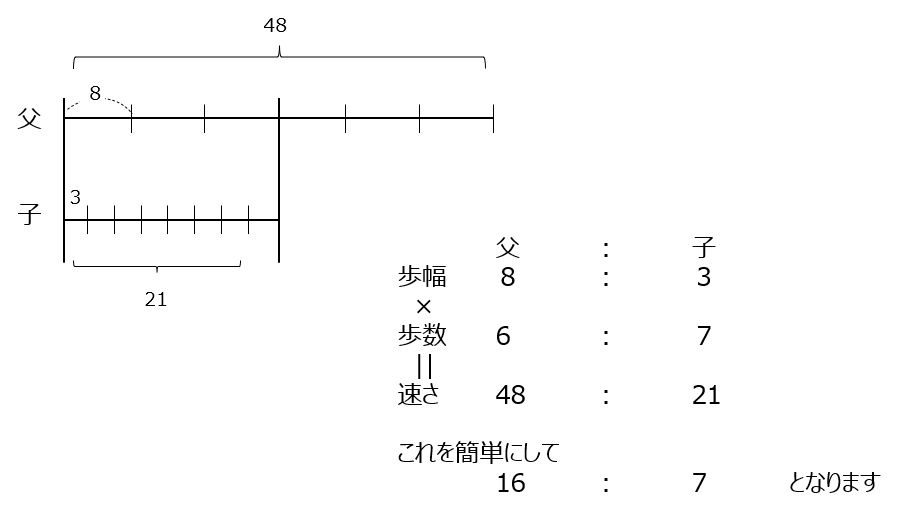
導入と基本③4⃣
歩幅、歩数から、速さの比を求めます。歩幅が逆比になる事に注意です。速さの比は距離の比ですね。

アプローチ①1⃣
(1)速さは変わっても距離ら変わらない事から比を使って解きます。時間の逆比が速さの比になります。速さの比の差が、問題文にありますね。
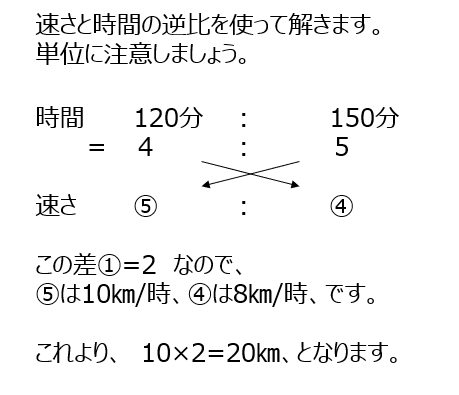
(2)は解く時に図に書いていますか?どちらが先に公園に着くか?どのあたりで出会うか、考えておきましょう。補足では比での解き方になります。
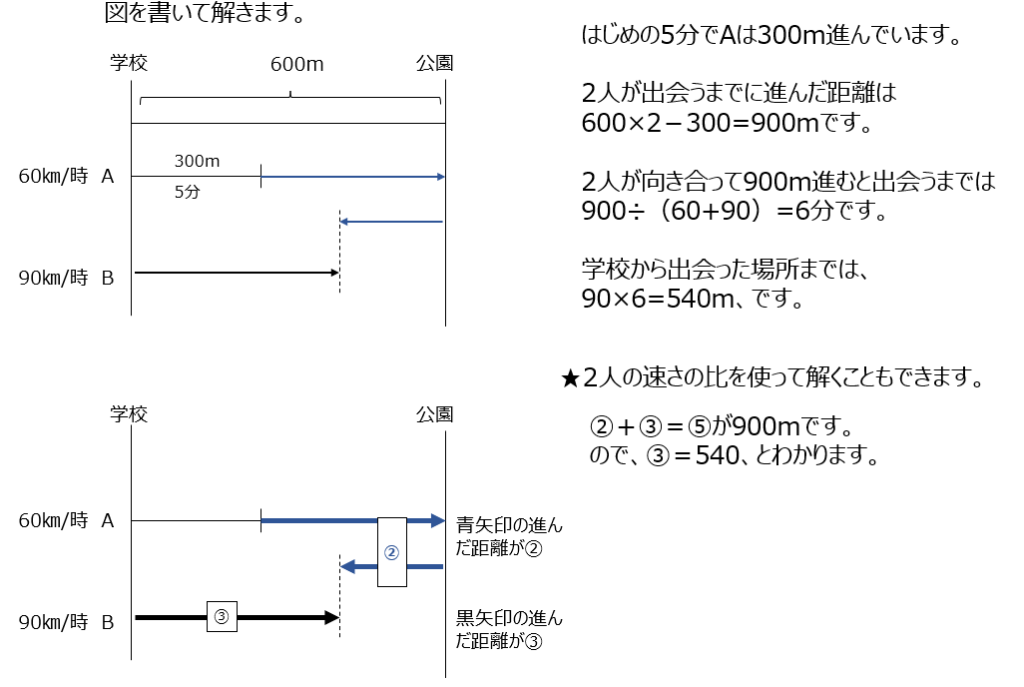
(3)でも図を書きましょうね。進んだ距離の差が5キロメートルから解きます。補足では比で解く解説があります。
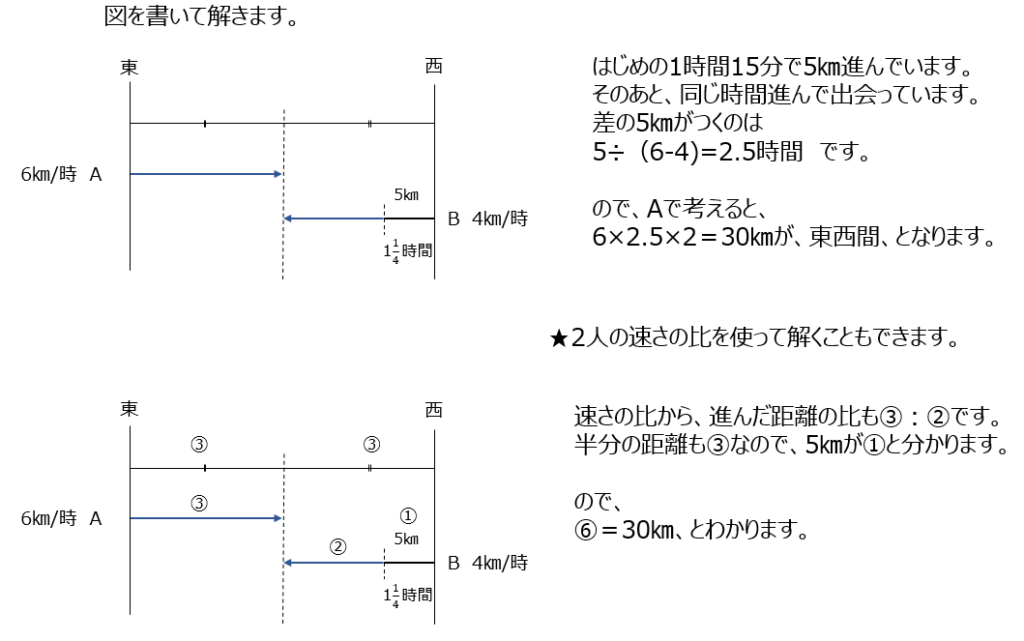
(4)では池の周りの問題です。どこで出会って、その時の差がどれくらいか、を図示すると分かりやすいですよ、動画は丁寧に説明あります。
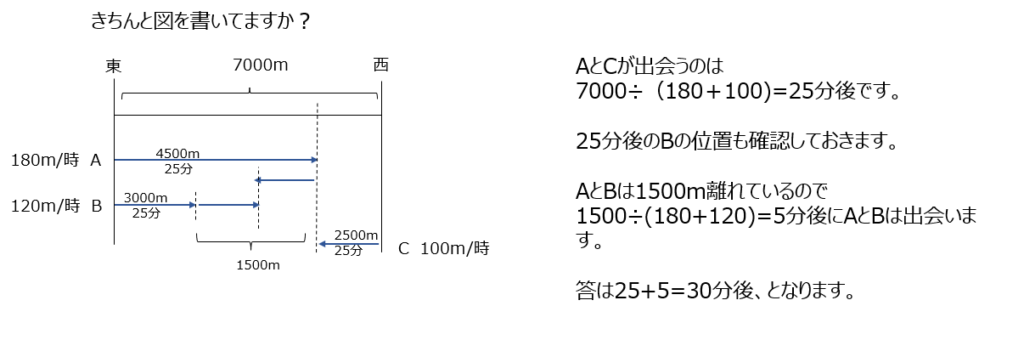
アプローチ②左1⃣
図に描く習慣はつきましたか?線分図では予定も書きます。遅れた時間の所で、速さの逆比で時間の比を使って解きます。
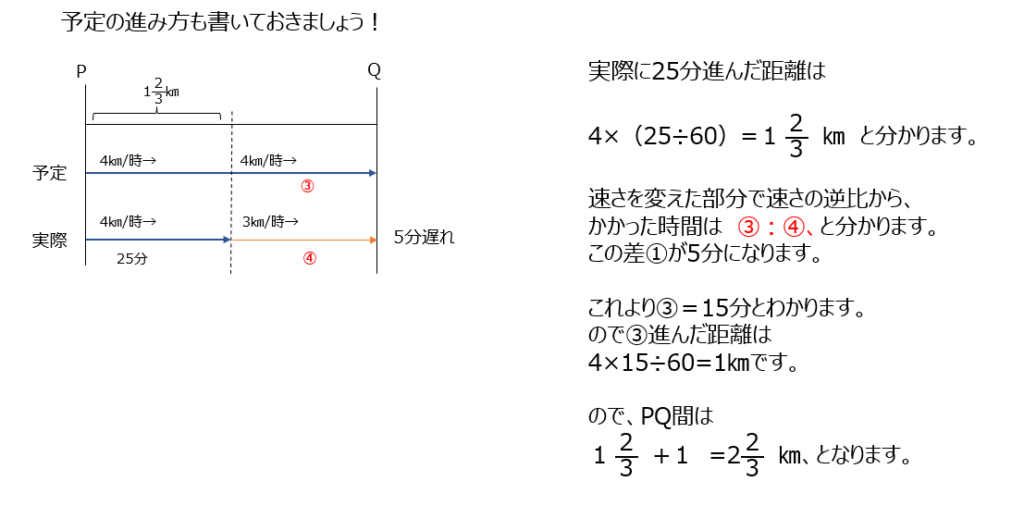
アプローチ②右1⃣
線分図にまとめます、予定と実際の線を書きます。かかった時間と速さ、の逆比を上手く使いこなせるようになりましょう!

アプローチ③左1⃣
図に書けましたか?
(1)始業時間の4分前からの10分後、です。
(2)では上の答えを使って、速さの逆比から時間の差を出して解きます、検算として、答えを確かめることもしましょうね。

アプローチ③右1⃣
進む距離が同じなので、逆比を上手く使います。
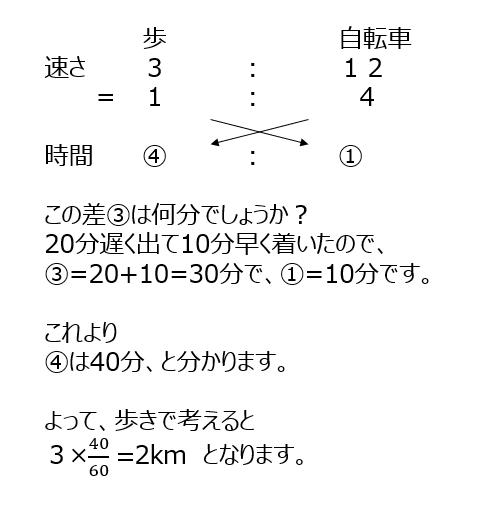
アプローチ④右1⃣
登りと降りを図に表せましたか?同じ距離のところは速さの逆比は、かかった時間になります。比が2つ出るので、消去算で解きます。

アプローチ④左1⃣
線分図に書いてまとめます、先程の問題とよく似ています。解法1では、同じように逆比からの消去算で解きます。

解法2では設問の流れに沿って解いていきます。距離の差になる部分に注目して解きます。
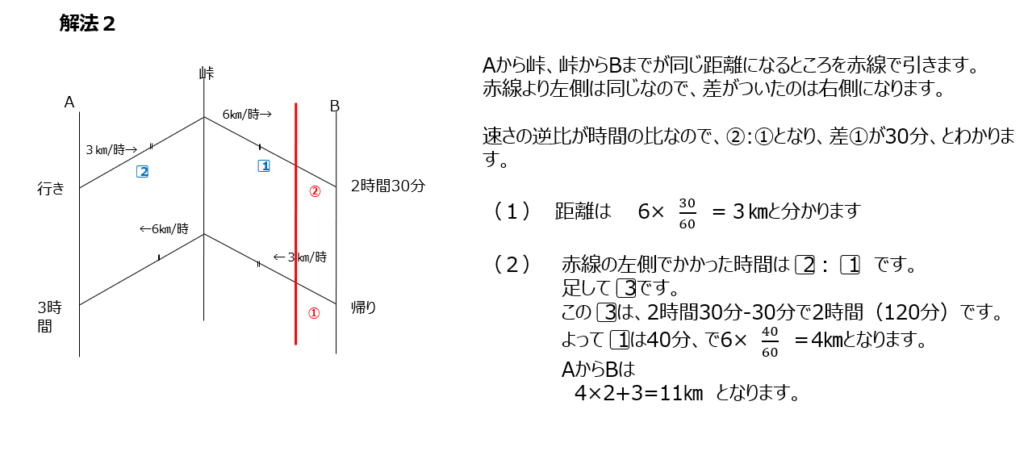
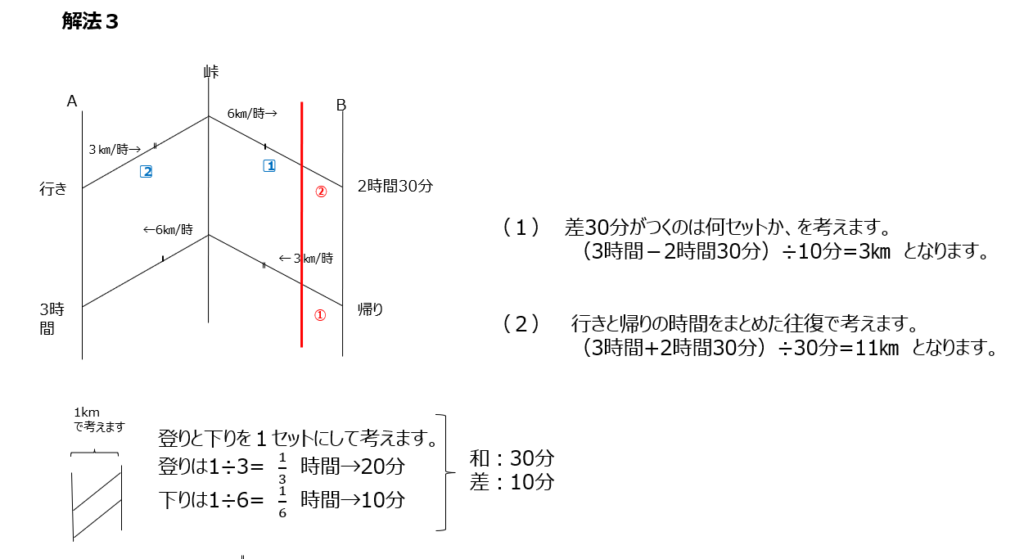
解法3では、登りと降りをセットで考えます。そのセットがなん個あるか、で考えます。
アプローチ⑥左1⃣
3人をそれぞれで考えます。AとB、BとCて時間の比から速さの比を出せますね。
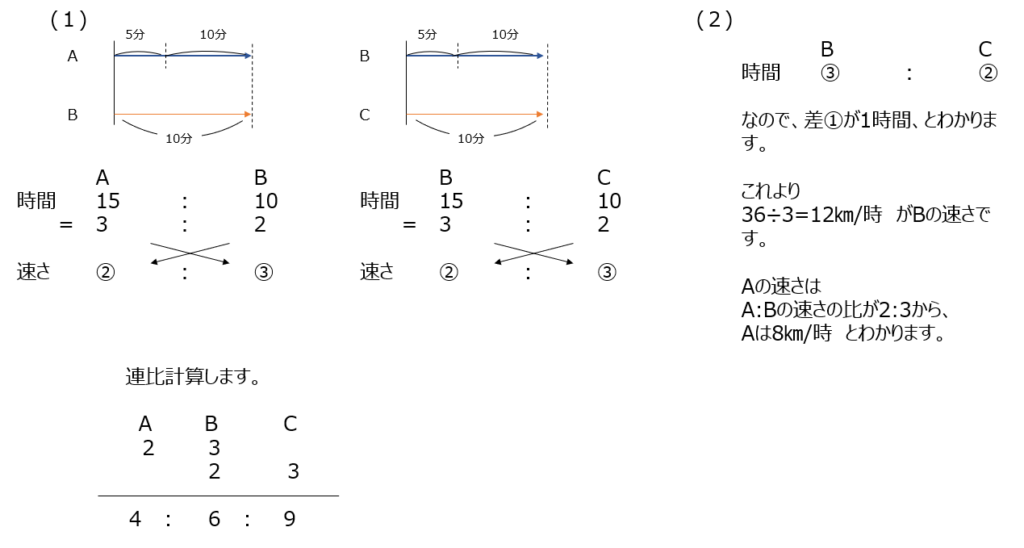
アプローチ⑥右1⃣
AとB、BとCの速さの比を出して、3人で連比にします。補足として、時間の比だけもで答えを出すこともできますね。

アプローチ⑦左1⃣
予定と実際ともし、の3つを表してみます。実際ともし、の速さの差の部分から時間の比の差がでますね。

アプローチ⑦右1⃣
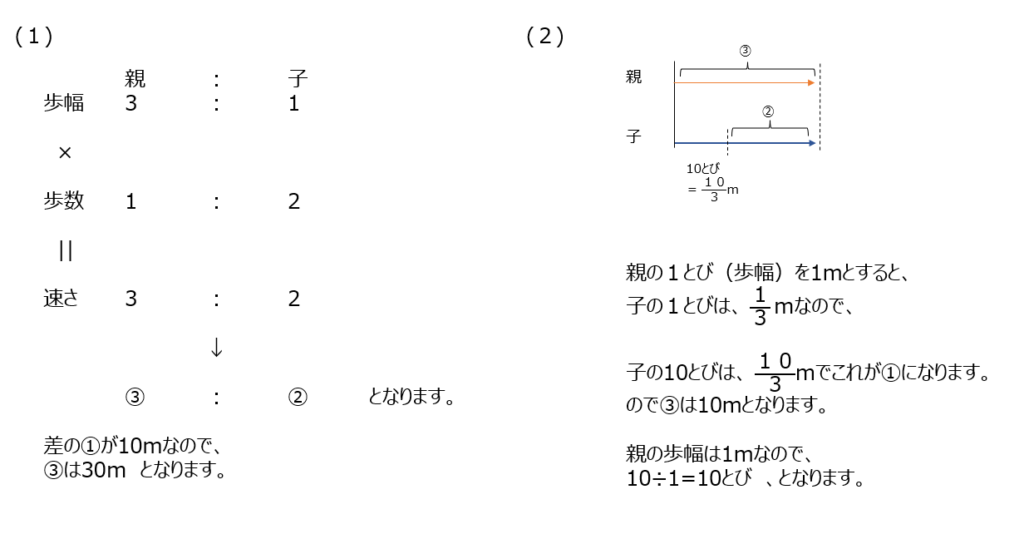
親うさぎと子うさぎの、歩幅、歩数からの速さ、を出します。線分図がわかりやすいですね。
アプローチ⑤右1⃣
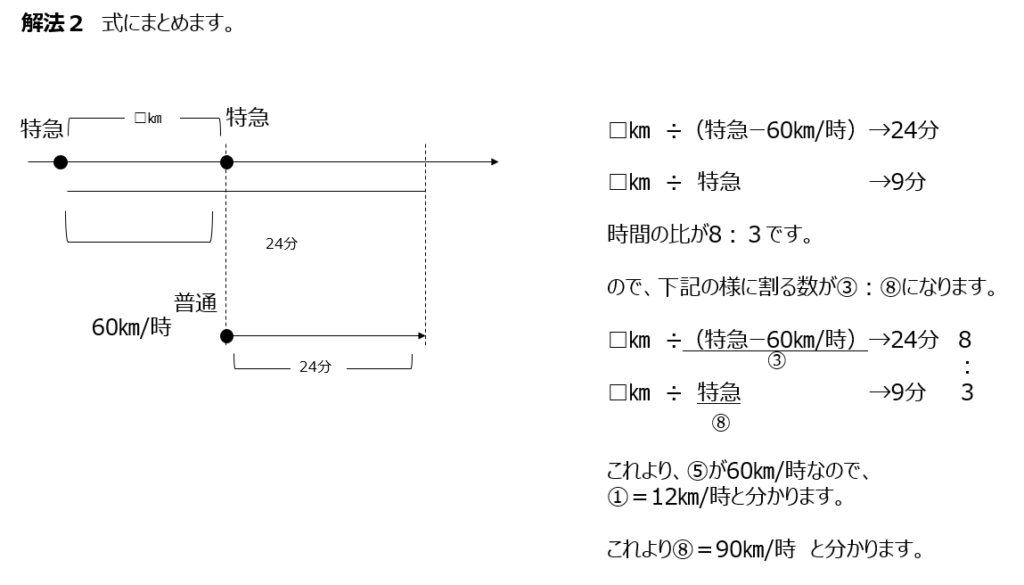
解法1では図に描いてまとめます、通過算ですかね。同じ距離の部分に着目ですね。解法2では式で考えます。式で逆比を使います。
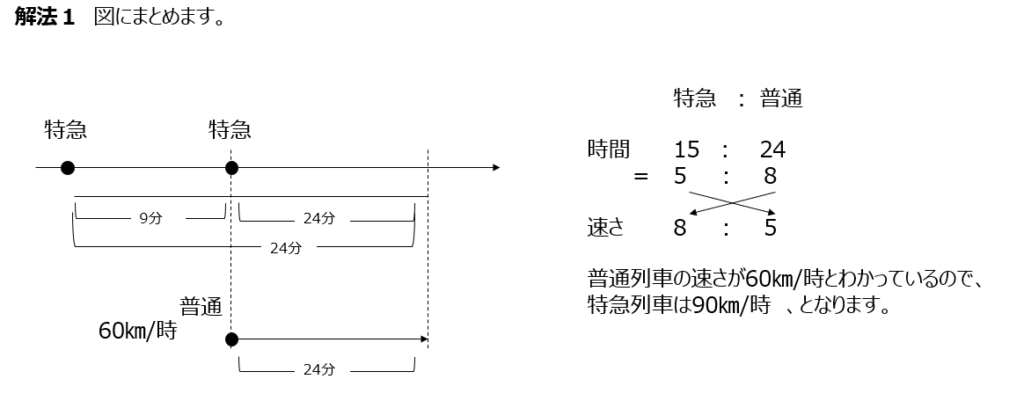
アプローチ⑤左1⃣
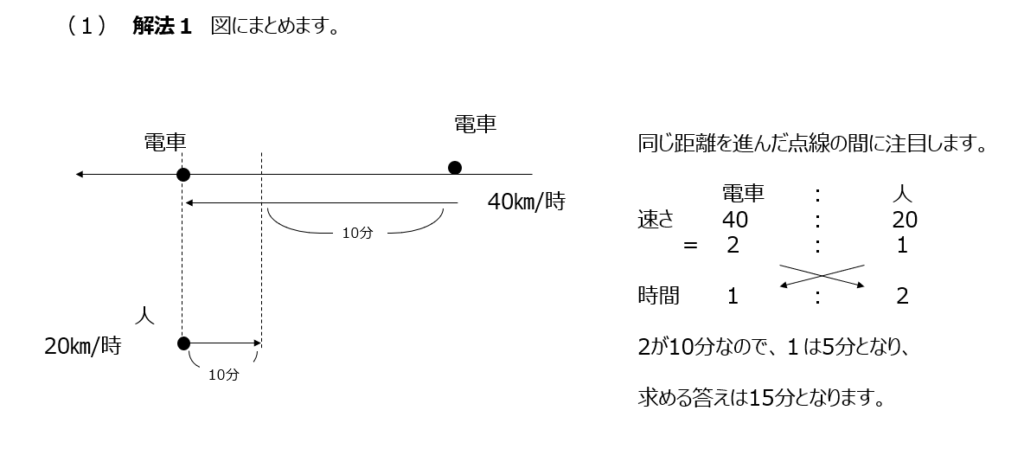
(1)解法1では図に表して考えてます。次の電車に会うまでですね。速さと時間がわかるので、逆比なども使えそうです。(2)式にまとめて考えてます。
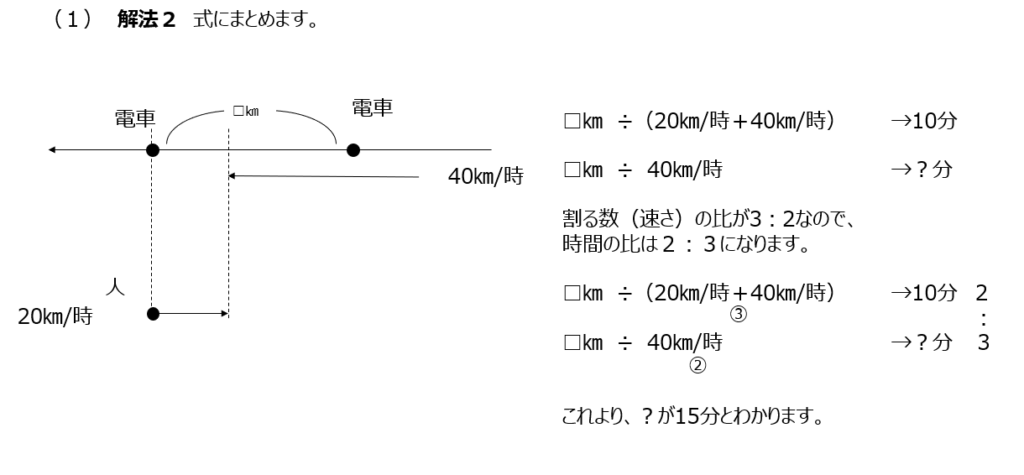

解法2では式にまとめて考えてます。
アプローチ⑧左1⃣
解法1では図にまとめます。人と電車とオートバイです。電車の長さを考えますので通過算ですかね、、、?動画では順番にわかりやすく解説あります。
解法2は式にまとめます。割り算の答えと商の逆比関係です。
実践編C1⃣
唯一分かっている7.5kmが割合でいくつか、を考えます。

実践編E1⃣
A君B君の歩幅と歩数から、速さの比を出します。逆比にして、時間の比を使います。
まとめ
わかってる数値が時間なら時間の比の差から求めます。距離が分かってるなら、距離の比の差から求めますよ。大きくは解き方は変わらないですが、経験して慣れたいですね。式にすると、割られる数が同じなら、商と答えは逆比になる、で考えます。この辺りも慣れちゃいましょう!
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント