算数の動画「平面図形(2)」を見ました。
前回と同じように補助線ありきの問題もありますね。しかも、算数なのに知識の問題もあります。こういうのは、知っていいるか知っていないのかだけで、解ける確率が変わってくるので、ぜひとも解き方を経験しておきたいところです!

アプローチ⑥の4題は、動画を見てやり方を丸暗記しておきましょう!
導入と基本③3⃣
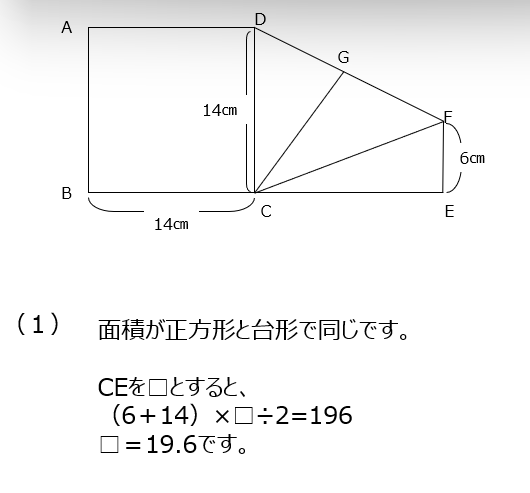
台形と正方形の面積が等しい問題です。(1)は面積が同じことから、台形の高さを求めます。(2)台形内の三角形で同じ高さの三角形から底辺の比で面積の比を求めて解きます。

アプローチ①左1⃣
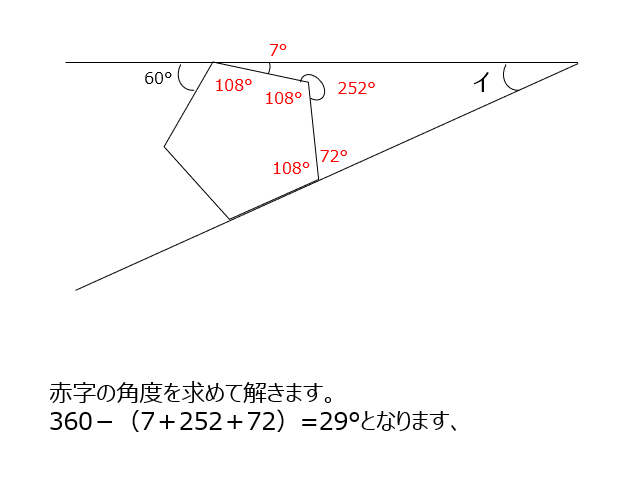
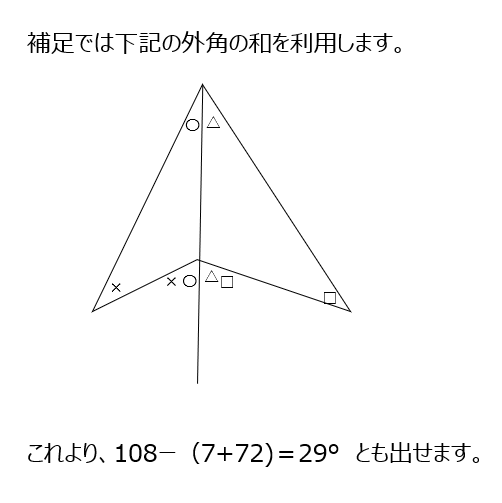
正五角形です、一つの内角は108°から、くぼみのある四角形から求めています。補足では、くぼみのある四角形の特徴を説明してくれています。知らない人は動画で確認しましょう。
アプローチ①右1⃣
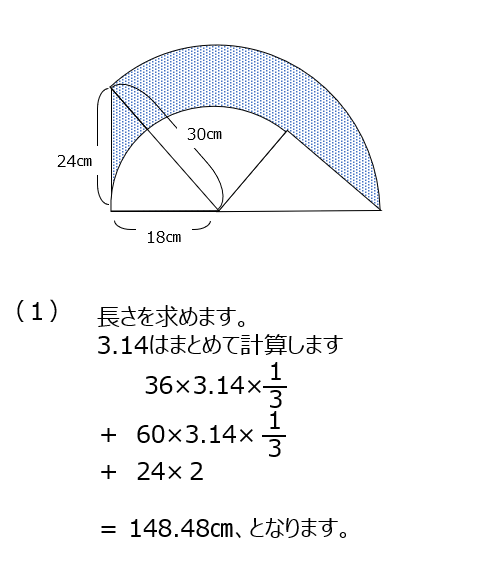
(1)は周囲の長さです。3.14の計算は最後にまとめてしますので、まずは式で書きましょう。直線部分も忘れずに計算に加えましょう。(2)は面積です、図形全体から不要部分を引く考え方で進めます。図の式を書いてみると、大きなおうぎ形から小さいおうぎ形を引くだけになります。

アプローチ②左1⃣
解法1では全体の面積がわかるので、補助線を引いて、各三角形の面積を出して、比で求めていく方法です。解法2では、面積を求めずに解きます。先ほどとは違う補助線を引いて、底辺の逆比から求めていきます、動画がとても分かりやすくて簡潔でした。
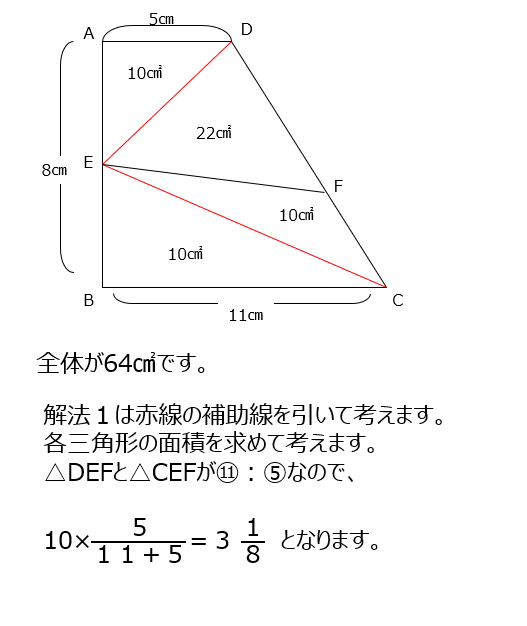
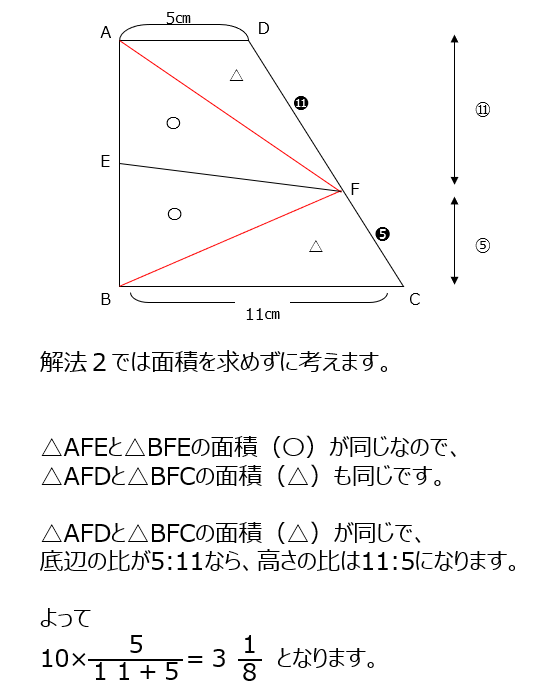
アプローチ③左1⃣
図形全体から引く方法で考えます。底辺と高さの比から、面積の割合を考えて解きます。
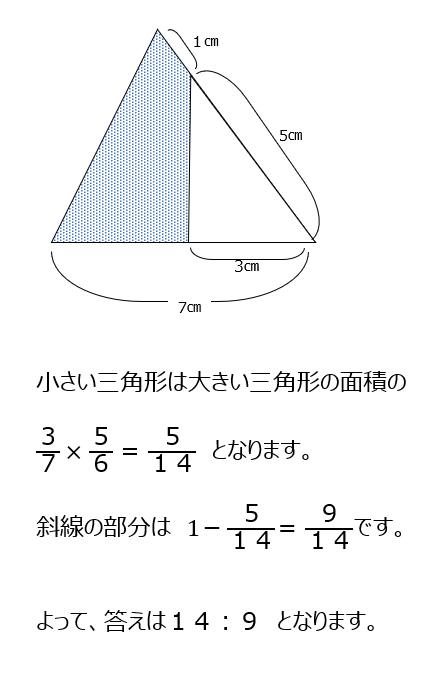
アプローチ③右1⃣
三角形が2倍の拡大図、となっていきます。長さが2倍、となっています(面積は2倍ではありません)。面積は4倍になっていきますね。各斜線部は、台形で見ると、高さが同じ底辺が違う三角形になっています。
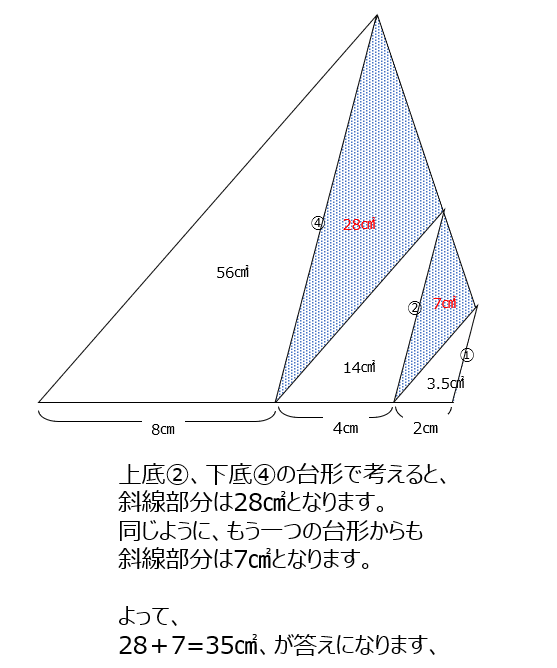
アプローチ④左1⃣
対角線で切られた正方形を数えます。横線をまたいで切られる、縦線をまたいで切られる、で考えます。横線、縦線の数を数えればよいですね。そうすれば計算で求めることができます。書かないで求めるようにしましょう。ピッタリの頂点を通る場合を考える必要もあります。途中で頂点を通るかどうかを考えて、最小単位の長方形がいくつあるか、で考えるようにします。ピッタリとなる点を引くことでも調整して求めることもできます。
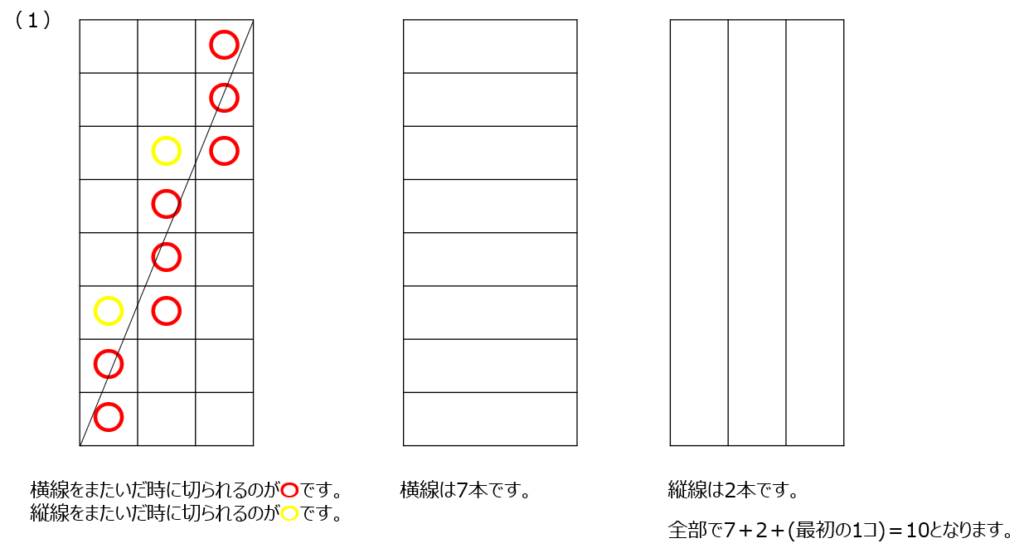
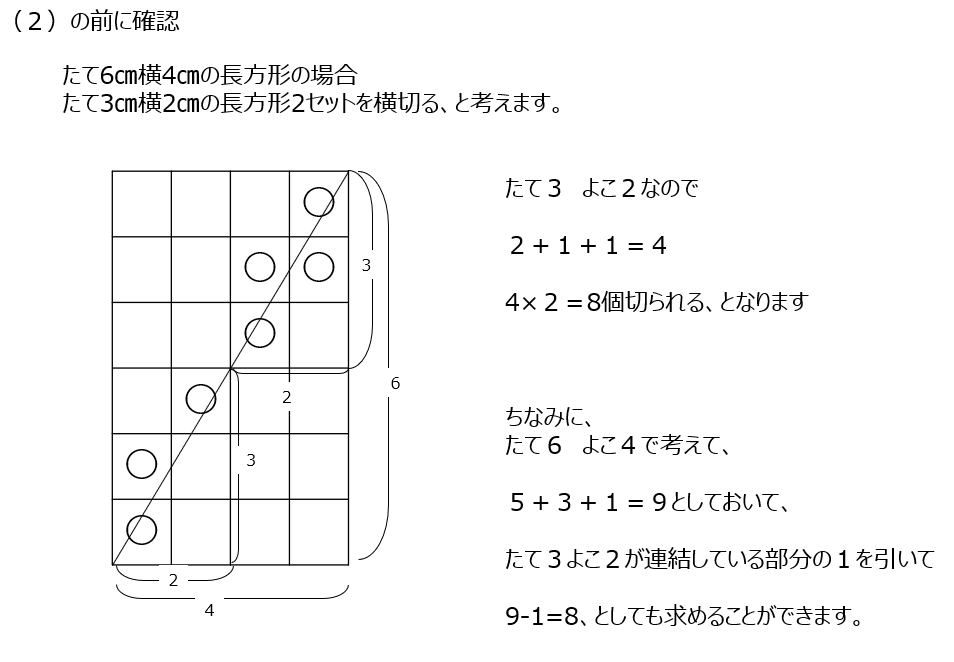
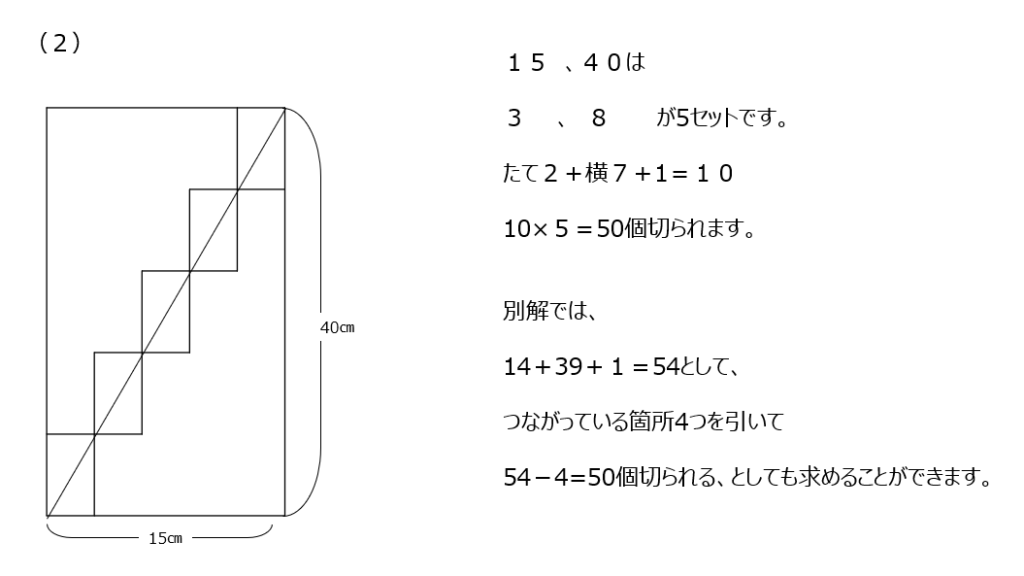
(2)では最小単位の長方形が5セットあります。最小単位が10なので、答えは50個ですが、ぴったりとなる4つを引いて求めることもできます。
アプローチ④右1⃣
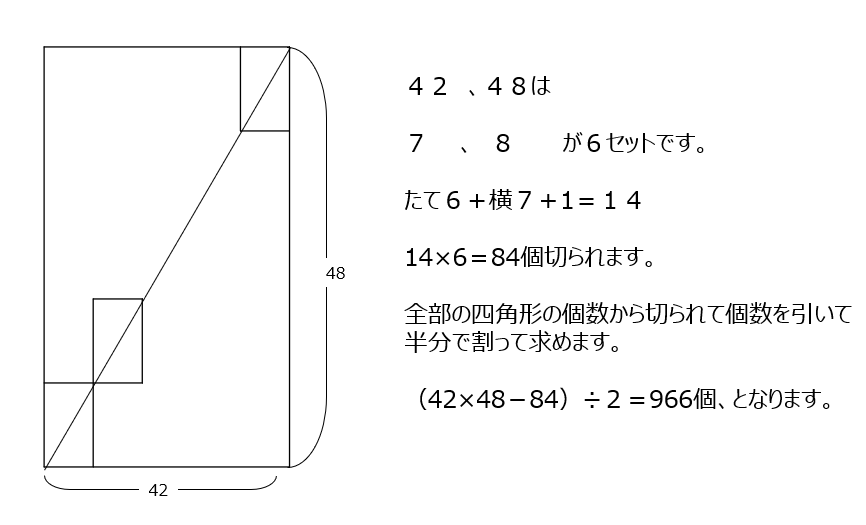
切られていない正方形を数えます。最小単位7cm8cmが6個あります。全部から、切られた分を引いて2で割ると、答えが求まりますね。
アプローチ④右2⃣
直角三角形を覆いつくすタイルの四角形の数を数えます。最小単位が2cm3cmです。斜め線で80枚が切られています。今までの考え方を使って解きましょう。
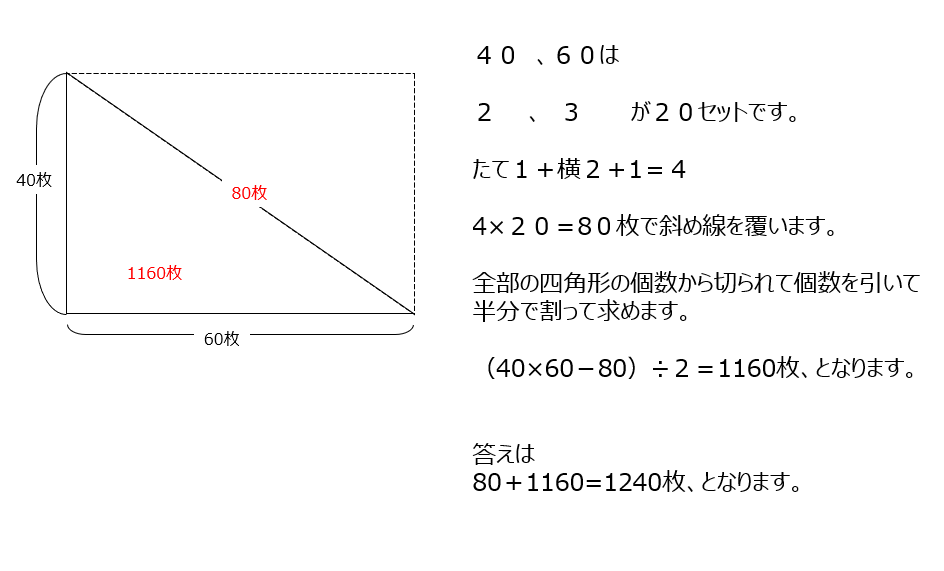
アプローチ⑤1⃣
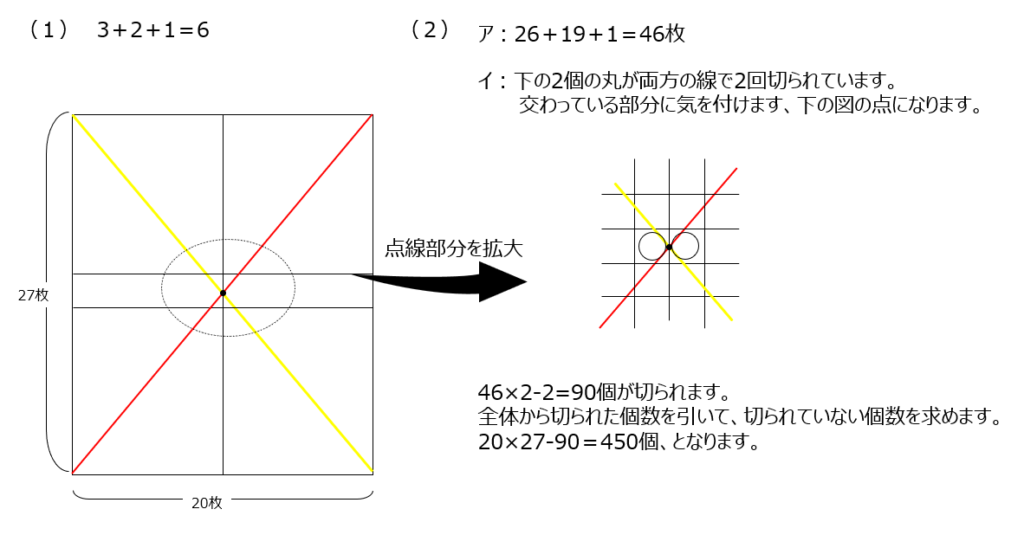
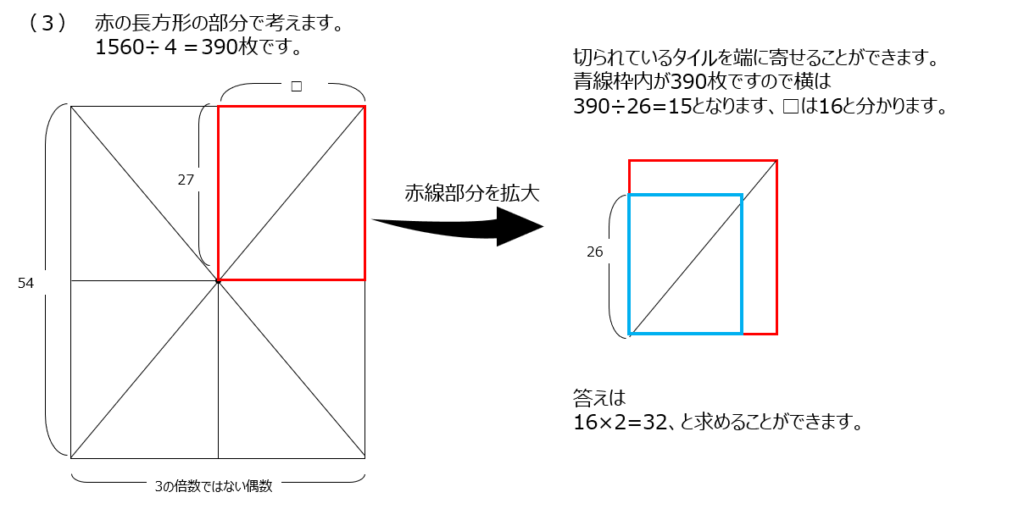
今までどおりで(1)(2)は解けます、対角線が二本引かれている問題が初見ですね。どちらの対角線でも切られている(重複している)タイルを求める必要があります。対角線が重なる中心部分を注目して考えます。今回の問題では、図で考えると、2枚が重複しているとわかります。(3)では長方形の長さが偶数なので、対角線が交わる部分はちょうど真ん中になっています。この場合は、4つの長方形で考えます。縦27枚、横が3の倍数でない偶数、の4等分された長方形です。切られたタイルを端に寄せて集約して考えます。集約すると、縦横が1ずつ小さくなります。動画がわかりやすいですよ。
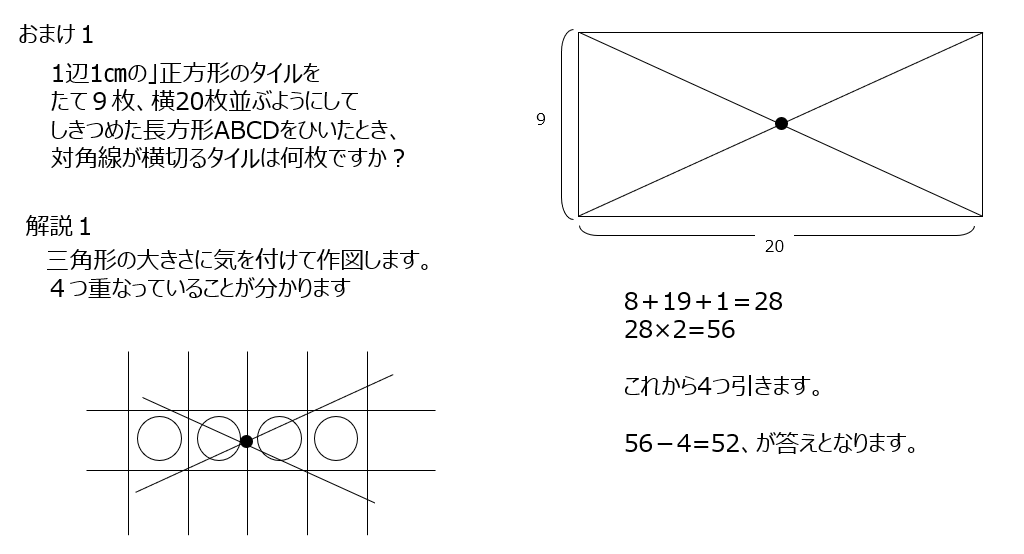
おまけ1、の問題があります。先ほどの問題と似ていますが、このおまけ問題は、横が偶数、縦が奇数の場合の考え方です。中心を注目して考えます。重複しているのが4枚ですね。
おまけ2、の問題があります。今回は縦横、ともに奇数の場合です。重複するのは5枚でした。
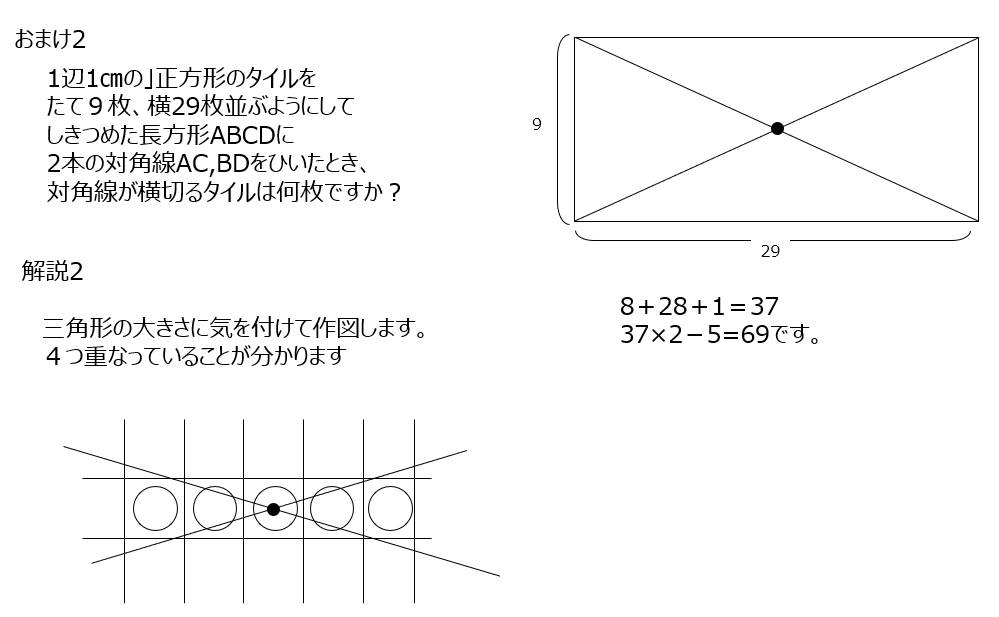
※中心部分を大体の図で考えていく、というのが、これらの問題のコツですかね~
アプローチ⑥1⃣
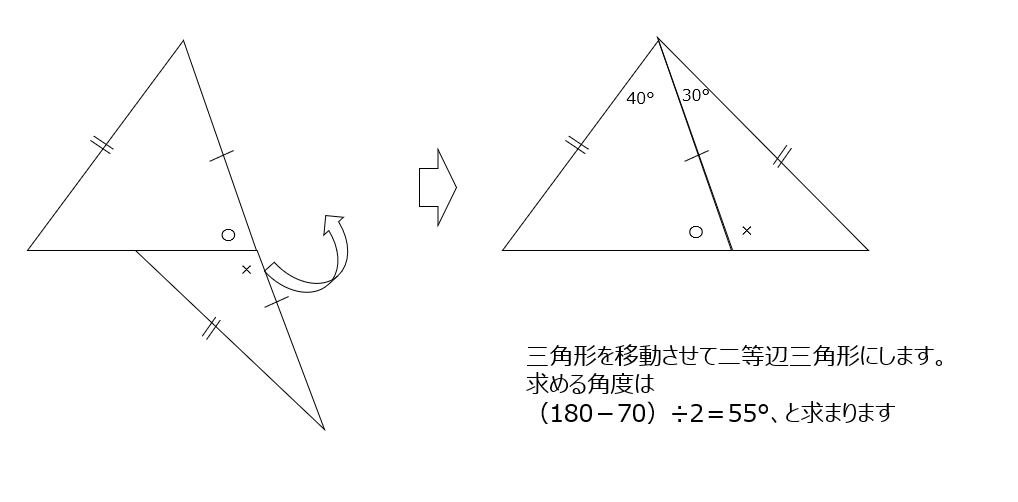
知識問題になります、テクニックを覚えましょう。cを中心に三角形を移動させる考え方です。移動させると二等辺三角形になっています。
アプローチ⑥2⃣
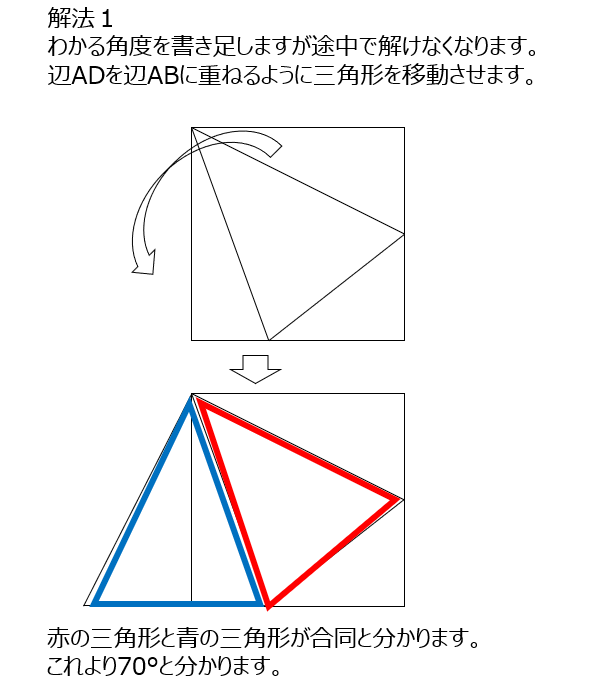
解法1では、まずわかる部分を書き込んで、Aを中心に三角形をぐるっと移動させる考え方です。移動させると、合同な三角形が現れます。解法2では三角形を内側に折り返す考え方です。注意はとがった2つの角度が45度の時だけの考え方です。

アプローチ⑥3⃣
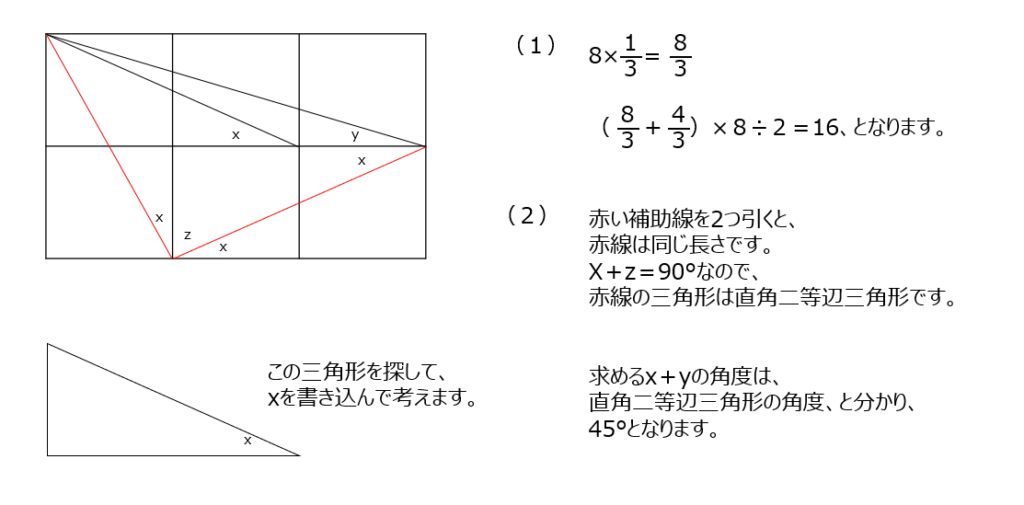
(1)は台形を求めます、相似の三角形ですね。ピラミッド型と砂時計で解きます。(2)が知識問題となります、それぞれの角はもとめられないです。xとyを寄せて考えます。xを含む三角形を移動させて、補助線を加えると、直角二等辺三角形がわかります。
アプローチ⑥4⃣
解法1では、BDを補助線として引いて、Dを中心に三角形ABDを回転させます。大きな直角二等辺三角形となります。解法2では、同じ図形を4つ合わせると正方形ができることから考えます。
実践編C1⃣
(1)は同じ面積の三角形から考えるとすぐに解けます。(2)おうぎ形と三角形の面積を式にして引き算で考えます。
実践編D3⃣
二等辺三角形の性質から考えます。底辺と高さが1:2になる三角形に切れます。考え方は、出せる部分から、いらない部分を引きます。台形から飛び出した三角形を引きます。
アプローチ⑥2⃣
今週の立体切断です、切られた個数を考えます。個別に切られた体積を考えて求めていきます。
今週の立体切断1⃣
三角錐の切断です。底面積、高さを長さの比で計算をします。どこを底面にするかで、高さが同じかどうか、などが変わってきます。
今週の立体切断2⃣
正四面体の切断です。(2)では平行な線を引いて切断面を考えます。斜めに傾いた角柱(斜角柱)の体積は底面積×高さ、で求められます、と問題文にありますので、これを使います。先ほど求めた三角錐と今回の三角柱の体積の割合を式で考えています。
まとめ
算数の知識問題としては、回転させたりして合同になる三角形や直角二等辺三角形を作ったりします。これは経験しておくかどうか、でかなり変わってきますので、何度か練習もしてみましょうね。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント