算数の動画「立体図形」を見ました。
立体図形に関しては想像力も必要で、小さい時から積み木とかさせておかないと、、、という意見もありますが、ある程度は小学校高学年からの努力でカバーできると思いますよ、しっかり頑張りましょう!

立体的に考える訓練をしておきましょうね
導入と基本③2⃣
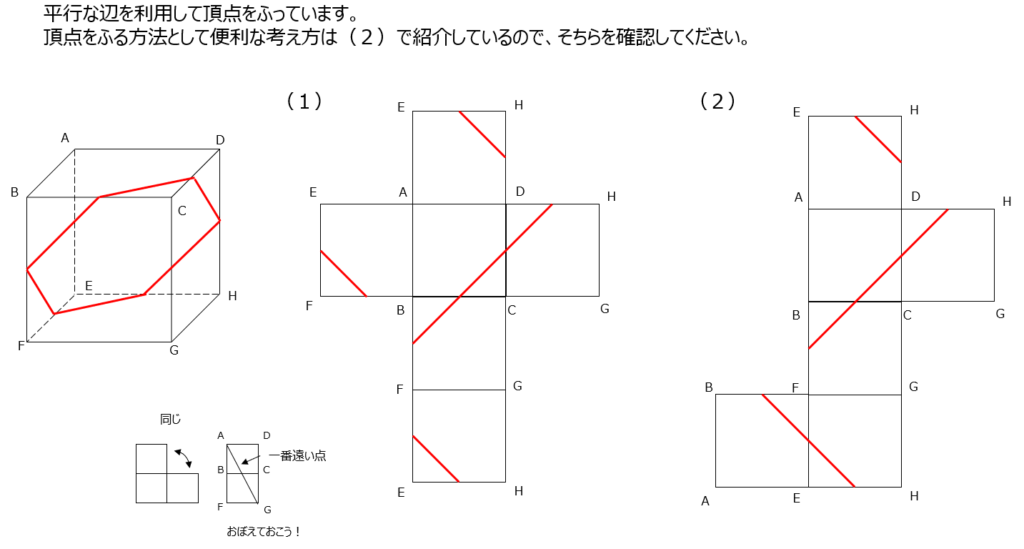
展開図に線を書いていきます。まず、立体体の頂点に記号をふって、それを展開図に書き込みましょう。平行な辺を利用して頂点をふっていきます。頂点をふる便利な方法は⑵で解説があります。1つの面に対してそれぞれ1本ずつ、展開図に辺が6本に引かれている事を確認する様にしましょう。
⑵では、覚えておくべき2つの展開図と、頂点の関係の説明があります。立方体で1番遠い頂点を展開図にふっていく方法です、わかりやすいですね。
アプローチ①A左2⃣
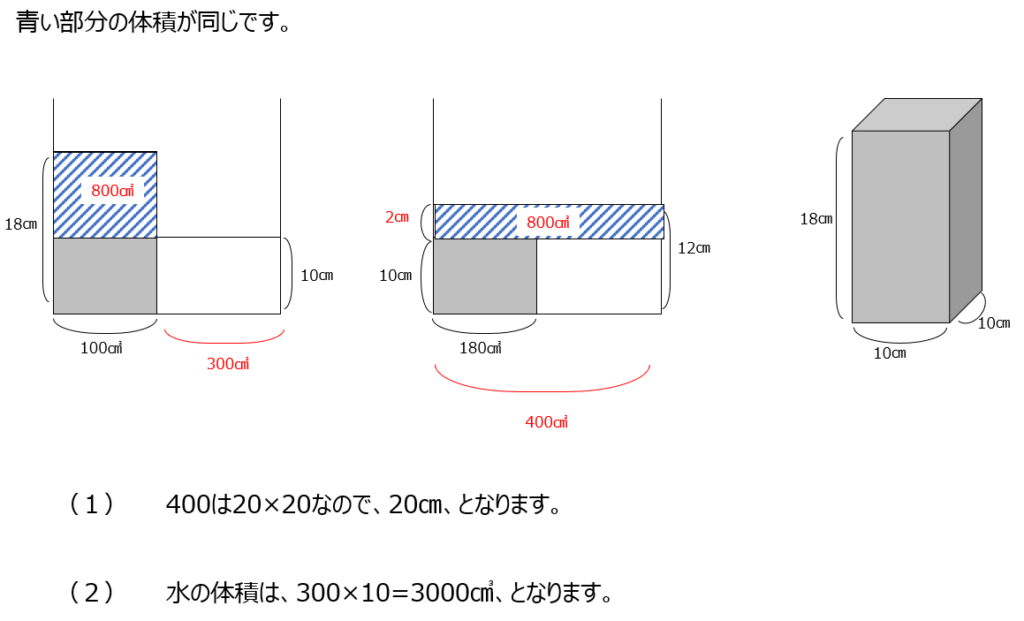
沈んでいる立方体の問題です、平面的に考えます。増えた水の体積がどこと同じか、を考えます。
アプローチ①A右1⃣
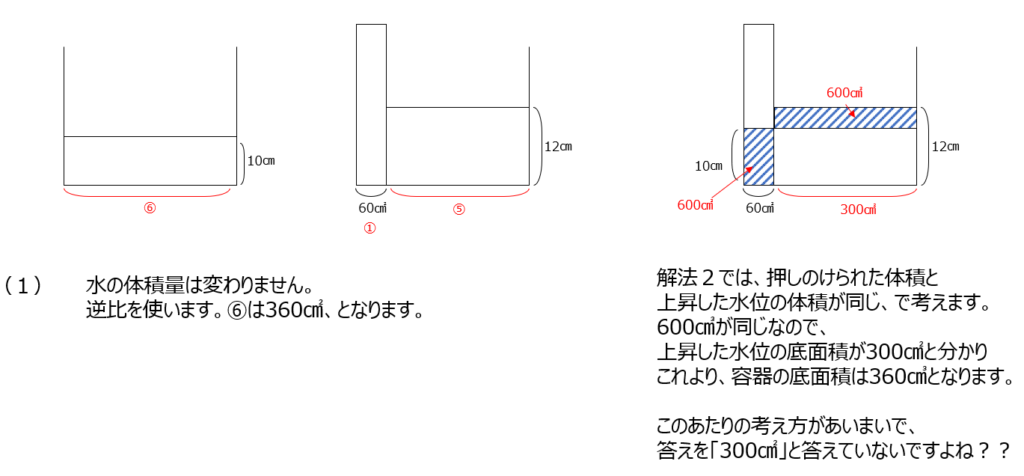
解法1では、水の体積は変わらないことから、高さの逆比が底面積の比になります。解法2では、押しのけられた体積がどこと同じか、を考えて解きます。動画では押しのけられてない共通の体積を考えて、計算が楽になる方法も紹介しています。
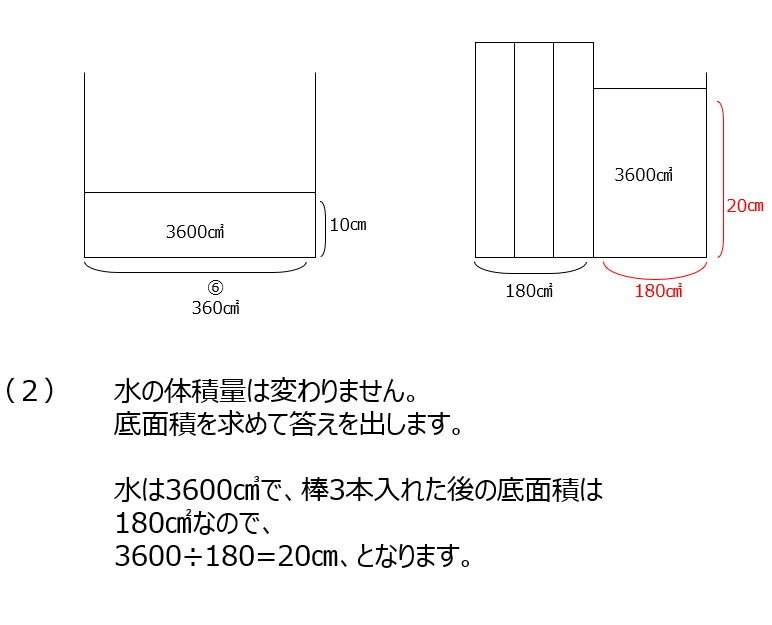
⑵では押しのけた体積と水の体積が変わらないことから解いています。
アプローチ①B1⃣
水が押しのけた体積の問題です。先程の問題の解法2の方法で解きます。押しのけた体積が同じことから、高さの比を用います。具体的な数値ではなく、比で計算を進めていきましょう。
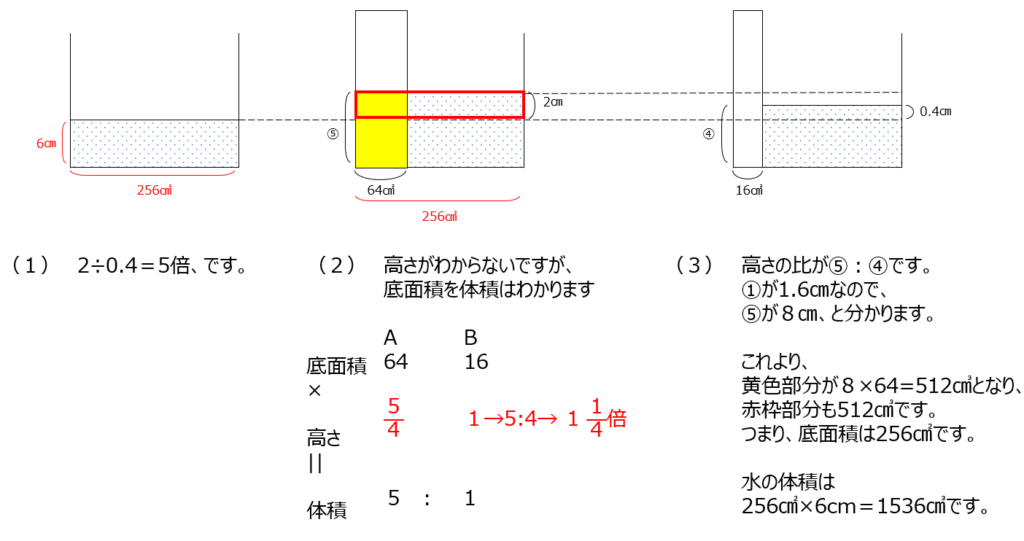
アプローチ②左1⃣
細い部分と太い部分の底面積の比を出してみます。二つを重ねてみて、足りない部分とはみ出てる部分が同じ体積、ということに着目します。動画では、色を付けてわかりやすく解説があります。

アプローチ②右1⃣
二つの図で比べる事ができる部分に着目します。円柱形の水と空気の部分の比を求めて考えます。
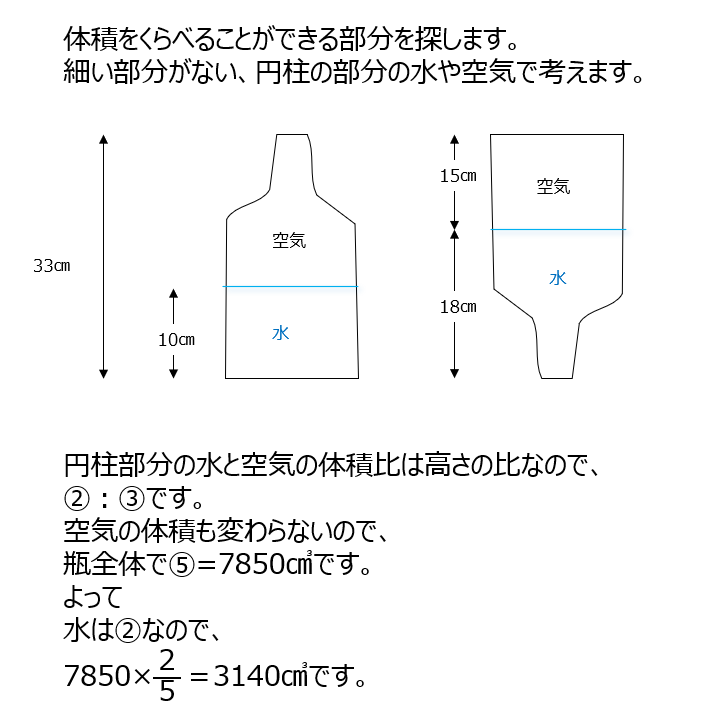
アプローチ③左1⃣
⑴では横から見て底面積が台形の体積を求めます。補足では、水が容器全体に対してどれだけ入っているか、を考えます。長さの比、底面積の比、から、高さが同じなので、体積の比から、全体の4分の3が水、とわかります。⑵では個別の長さを求めて進めても良いですが、全体の4分の3が水、というのは変わらない事を使うと、簡単に求める事もできますよ。⑶でもら体積が全体の4分の3、をつかうと、面積比も4:1なので相似比は2:1ですね。

アプローチ③右1⃣
円すいと円すい台の体積の比を求めます、それぞれを求めるのではなく、比を用いて解きます。相似比を3回かけると体積比になりますね。大きい円錐に水を入れて考える問題でも、体積の比を用いて解きます。円錐の体積比、で比べます、台形の体積比ではないですよ。
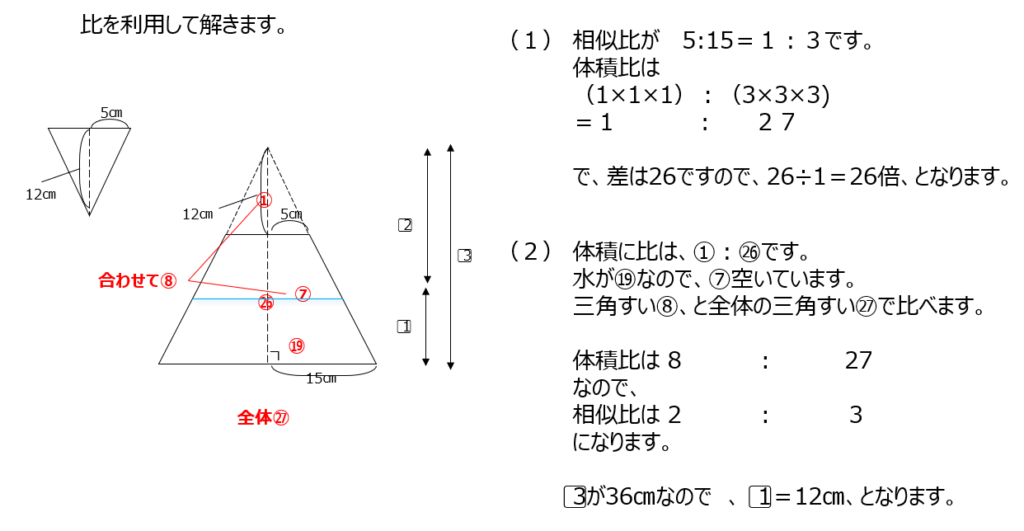
アプローチ④左1⃣
四角すいを展開した図から、長さを求めます。高さが展開図のどこにあたるか、を考えます。
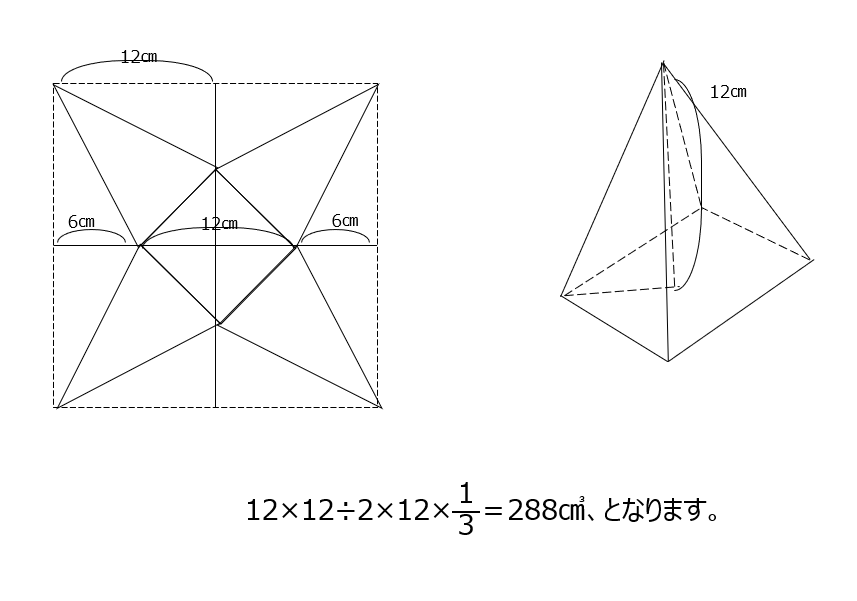
アプローチ④右1⃣
展開図から六角柱、とわかります。どの辺にくっついているべきものが足りないかを探します。4通りありますので、動画でも確認してみましょう。(2)辺の数は、6×3で出しましょう。(3)18か所ののりしろが必要ですが、すでに引っ付いている部分は引きます。補足では、くっついている部分を計算で出す方法を教えてくれています。(つながりの数)=(面の数)ー1でも求められます。
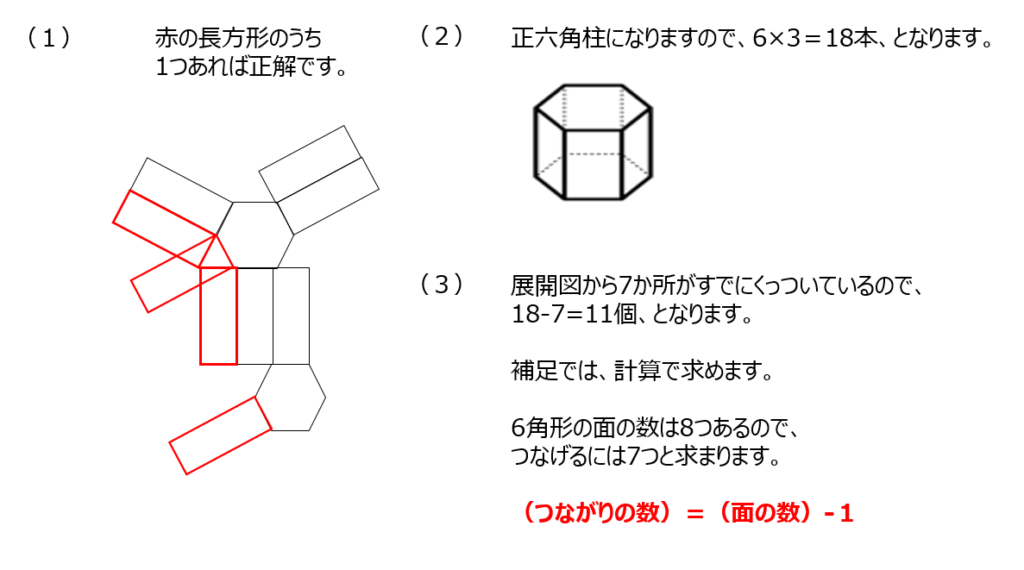
アプローチ⑤左1⃣
三角すいの体積を比べます。体積を求めるための長さの掛け算を比にします。
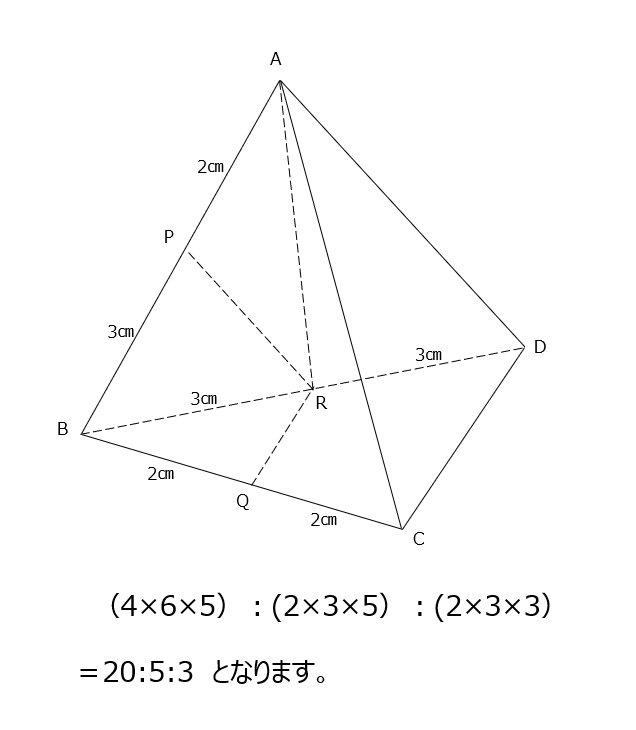
アプローチ⑤右1⃣
立方体の切り口を展開図で表す問題です。まずは頂点の名前を展開図に記載して考えましょう。斜線はF側にあることで間違えずに引くようにしましょう。(2)では三角すい台を求めて考えますが、体積比を用いることで計算を楽にします。
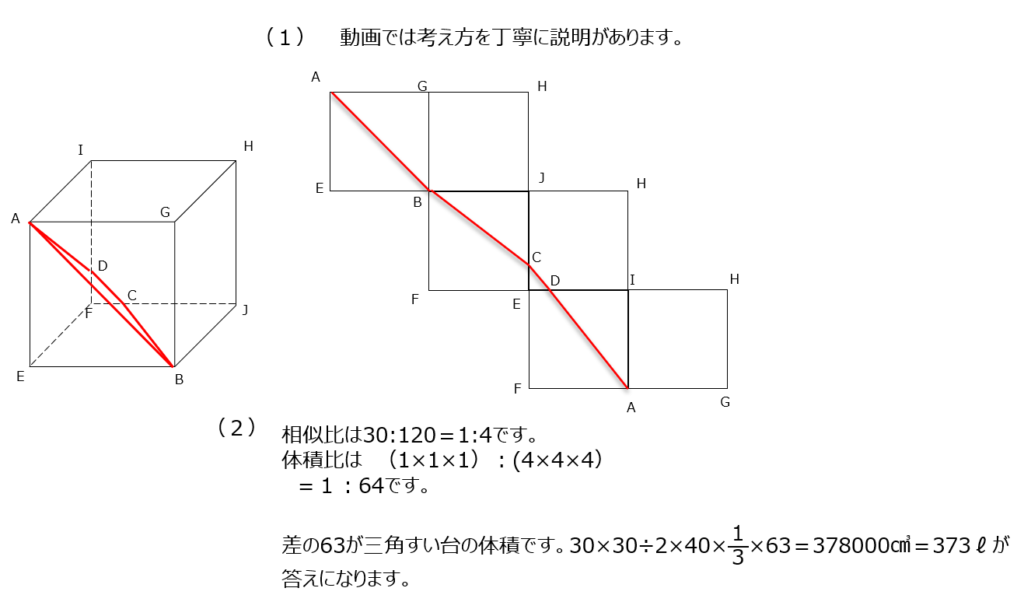
アプローチ⑥A1⃣
四角すいの切断問題です。三角形を取り出して平面で考えていきます。(1)では砂時計型の三角形の相似で考えます(2)でも同じように砂時計型の三角形の比を用います。(3)(4)では体積比を求めていきますが、同じように切り口の三角形を平面で考えていきます。
アプローチ⑥B1⃣
求める立体を2つに分けて考えるのは今まで通りですね。2つに分ける真ん中の三角形OACで考えます。先ほどと同様に線を延長して砂時計型の三角形で考えます。片方の体積を求めて2倍することで求まります。動画のおまけの発展問題では、数値を一部変更した問題です。先ほどと同じように2倍にはならないですが、それ以外は同じです。この問題ができれば、今日の学習内容の理解はOKになるような問題です。ぜひチャレンジしてほしいですね。
実践編C1⃣
見取り図ではわかりずらいので、上から見た図で考えます。
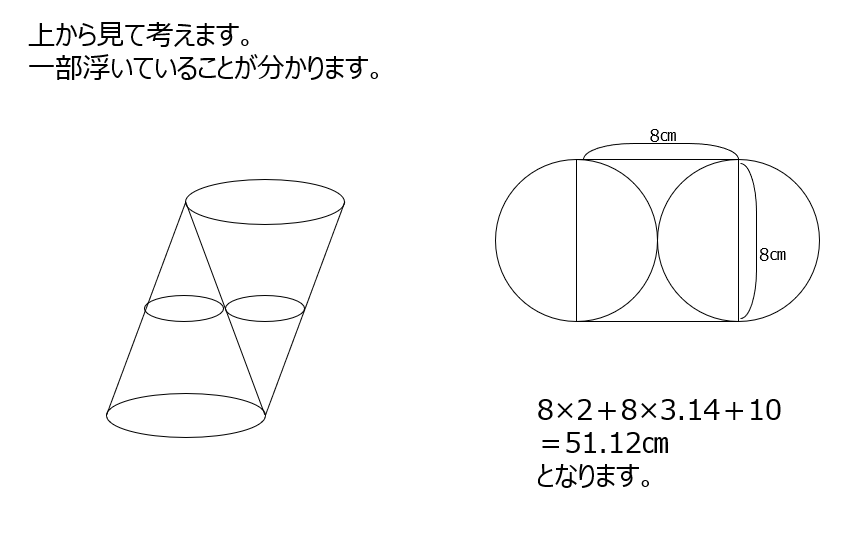
実践編E1⃣
立方体の角を切り落としていくイメージの問題です。正四面体ができます。覚えておきましょう!
アプローチ⑧1⃣
立方体を積み上げた立体を切断する問題です。立方体が4つあるとして考えたほうがわかりやすいです。
アプローチ⑧2⃣
立方体を積み上げた立体を切断する問題です。 升目の中途半端な部分の切り目になるところを丁寧に考えましょう。
今週の立体切断1⃣
(1),(2),(3)で出した体積を(4)で使って求めます。
今週の立体切断2⃣
(3)の体積を求める問題です、回答とは違う方法を動画で説明があります。直接求めていく方法です。立方体の4隅を切り取ると残る四角すいは全体の三分の一になることを使います。
まとめ
求める体積を比を用いて解いたり、2つや3つの切り分けて考えたりする問題を学びました。長さの比から体積にする考え方は、計算が楽になりますね。展開図については、導入と基本で丁寧に解説あるので、是非できるようにしましょう。
最後まで読んで頂きありがとうございました。
下記に他の動画解説のページもありますので、紹介させてください。
参考になるとうれしいです。




コメント